源码下载地址@[toc]
源码下载地址
项目介绍
- LDPC码背景及概要
LDPC是Low Density Parity Check Code英文缩写,意为低密度奇偶校验码,最早在20世纪60年代由Gallager在他的博士论文中提出,但限于当时的技术条件,缺乏可行的译码算法,此后的35年间基本上被人们忽略。直到1993年Berrou等人发现了Turbo码,在此基础上,1995年前后MacKay和Neal等人对LDPC码重新进行了研究,提出了可行的译码算法,从而进一步发现了LDPC码所具有的良好性能,迅速引起强烈反响和极大关注。经过十几年来的研究和发展,研究人员在各方面都取得了突破性的进展,LDPC码的相关技术也日趋成熟,逐渐有了商业化的应用成果,如今LDPC码已经作为众多新一代通信标准中的信道编码方案:DVB-S2 (Digital Video Broadcasting)、IEEE 802.3an (Ethernet)、IEEE 802.16e (WiMax)、IEEE 802.11n (WiFi)、3GPP 5G标准。
LDPC码是一种稀疏校验矩阵线性分组码,在LDPC编码中,会用到一个叫做H矩阵的校验矩阵(Parity Check Matrix),该校验矩阵为稀疏矩阵。
LDPC编码分为正则编码和非正则编码。正则编码中,校验矩阵的每行和每列中1的个数是固定的。非正则编码中,校验矩阵的每行和每列中1的个数不固定。
LDPC解码过程中,主要包括了两方面内容:硬解码(Hard Decode)和软解码(Soft Decode). LDPC解码的方法就是收到码字之后,与校验矩阵H相乘,如果是0矩阵,则说明收到的是正确码字。反之,则不正确码字,再根据相乘结果进行进一步纠错解码
- 仿真要求及内容
本次仿真要求通过MATLAB软件对LDPC码进行编译码仿真,通过计算模拟求解归一化最小和算法α参数的最佳值和偏置最小和算法β参数的最佳值,并仿真出四种不同的译码算法下的误码率和误帧率曲线。实验的要求如下:
采用系统码设计,信息序列长1008比特,码长2016比特,码率1/2,即
N = 2016 , K = 1008 , R = 1 / 2 N=2016,\ K=1008,\ R=1/2 N=2016, K=1008, R=1/2
给定的编码矩阵 H_block 是一个18x36的矩阵(Matrix(2016,1008)Block56.mat文件中也是只有18x36个数据),矩阵中每个元素 H(i,j) 是大小为 z*z 的循环移位矩阵(给定z=56),行重为1,它的值表示该矩阵的循环位移偏移量,也是第一行中元素1所处的列的位置,若H(i,j)值为0,表示是全0矩阵。
给定 矩阵,根据给定规则求解校验矩阵 。
根据校验矩阵直接进行编码:利用输入信息比特序列 s s s和校验矩阵 H H H求得校验比特序列 , 即为编码序列。
编码序列采用BPSK调制并通过AWGN信道添加噪声。
完成以下四种译码算法的MATLAB代码实现
和积算法(Sum-Product, SP)
最小和算法(Min-Sum, MS)
归一化最小和算法(Normalized Min-Sum, NMS)
偏置最小和算法(Offset Min-Sum, OMS)
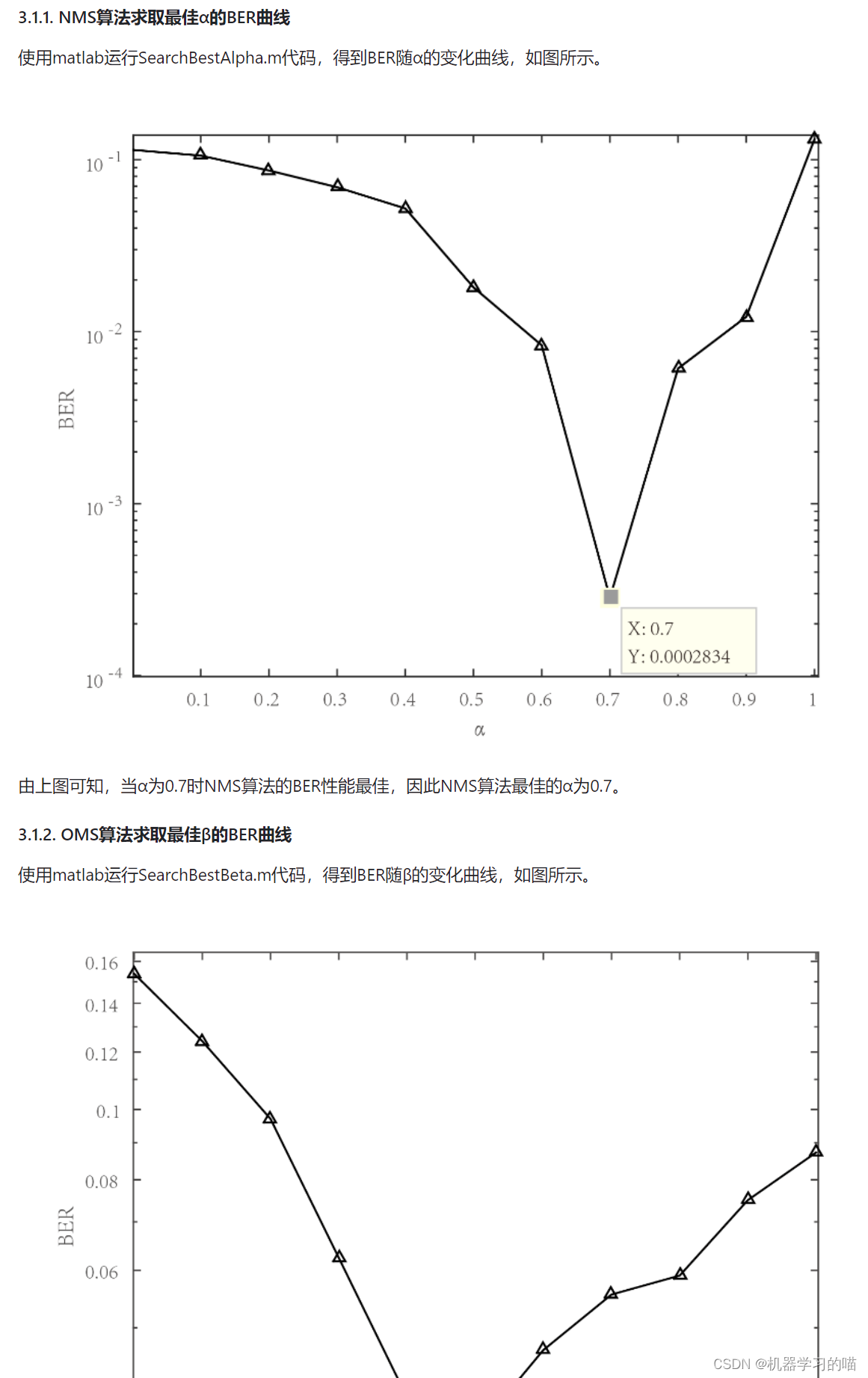
对于归一化最小和算法和偏置最小和算法,选定一个Eb/N0(1dB附近),仿真BER得出α和β最佳值。α和β取值范围均为0到1,步进为0.1,α和β的BER曲线各画一张图。
仿真得出Eb/N0在-1dB到2dB(步进0.5dB)时四种译码算法的BER和FER,两个修正最小和算法的α和β都取最佳值。应画BER一张图,FER一张图,每一张图都包含四种算法。
2.1. LDPC编码算法
LDPC码通常由校验矩阵H进行定义。尽管线性分组码可以使用传统的生成矩阵进行编码,但是要通过H求解G在实现上较为困难,因此根据校验矩阵直接进行编码。本次作业采用系统码,且校验矩阵H可分为两部分
H
=
[
H
p
∣
H
s
]
,其中
H
p
对应校验比特部分,对
H
s
应信息比特部分;编码序列可分为
x
=
[
p
s
]
H=\left[ H_p|H_s \right] ,其中 H_p 对应校验比特部分,对 H_s 应信息比特部分;编码序列可分为 x=\left[ p\ s \right]
H=[Hp∣Hs],其中Hp对应校验比特部分,对Hs应信息比特部分;编码序列可分为x=[p s],其中
p
p
p为校验比特序列,
s
s
s为信息比特序列。本作业的编码部分有两种编码算法用以实现LDPC编码。
2.1.1. LDPC编码算法1
由于校验矩阵H的性质:
H x T = 0 Hx^T=0 HxT=0 因此可采用基于H矩阵的通用LDPC编码方法:
H x T = 0 ⇒ [ H p , H s ] [ p T s T ] = 0 ⇒ p = s H s T ( H p T ) − 1 Hx^T=0\Rightarrow \left[ H_p,H_s \right] \left[ \begin{array}{c} p^T\ s^T\ \end{array} \right] =0\Rightarrow p=sH_{s}^{T}\left( H_{p}^{T} \right) ^{-1} HxT=0⇒[Hp,Hs][pT sT ]=0⇒p=sHsT(HpT)−1 由上式可知,本算法需要 H p H_{p} Hp可逆,且上式p为1x(N-K)向量、s为1xK向量、 H s T H_{s}^{T} HsT为Kx(N-K)矩阵、 H p T H_{p}^{T} HpT为Kx(N-K)矩阵,因此该算法需要 K ( N − K ) + ( N − K ) ( N − K ) K(N - K) + (N - K)(N - K) K(N−K)+(N−K)(N−K)次比特乘法运算和 ( K − 1 ) ( N − K ) + ( N − K − 1 ) ( N − K ) (K - 1)(N - K) + (N - K - 1)(N - K) (K−1)(N−K)+(N−K−1)(N−K)次比特加法运算。
2.1.2. LDPC编码算法2
将基于H矩阵的通用LDPC编码方法进行分解,具体步骤如下:
首先利用信息序列s计算中间结果 w = s H s T w = [ w 1 , w 2 , ⋯ , w m b z ] w=sH_{s}^{T}\quad w=\left[ w_1,w_2,\cdots ,w_{m_bz} \right] w=sHsTw=[w1,w2,⋯,wmbz]
利用编码序列x计算校验比特 H x T = 0 ⇒ [ H p , H s ] [ p T s T ] = 0 ⇒ p H p T = s H s T Hx^T=0\Rightarrow \left[ H_p,H_s \right] \left[ \begin{array}{c} p^T\ s^T\ \end{array} \right] =0\Rightarrow pH_{p}^{T}=sH_{s}^{T} HxT=0⇒[Hp,Hs][pT sT ]=0⇒pHpT=sHsT 故可得: KaTeX parse error: Expected '}', got '\right' at position 175: …\ \end{matrix} \̲r̲i̲g̲h̲t̲.
此算法易错处为: 上式中运算过程是应由右侧值决定左侧值,即只有当右侧表达式中各变量的值被赋过一次值时才能对左侧值赋值。例如:
当i=1时,w1已知,p1=w1
当i=2时,w2已知,但p(mb-1)*z并没有值,因此此时还不能立刻求p2,而是应该求p(z+1)=w(z+1) 模二求和 p(1)。即: -当i=(z+1)时,w(z+1)已知,p(1)已知,p(z+1)=w(z+1) 模二求和 p(1)
…
组合p与s
x
=
[
p
s
]
x=\left[ p\ s \right]
x=[p s] 将校验比特序列p和信息比特序列s组合即得到编码序列x。
检验 由于编码过程利用的是
因此,得到编码序列x后需要对x进行检验,保证其满足上式即表明完成了正确编码工作。
2.1.3. 两种算法比较
两种算法在时间复杂度上的区别如图所示(
(
H
p
T
)
−
1
\left( H_{p}^{T} \right)^{- 1}
(HpT)−1可以离线求解,所以不占用复杂度), 两种编码算法的时间复杂度对比
项目功能
界面预览
项目备注
1、该资源内项目代码都经过测试运行成功,功能ok的情况下才上传的,请放心下载使用!
2、本项目适合计算机相关专业(如计科、人工智能、通信工程、自动化、电子信息等)的在校学生、老师或者企业员工下载学习,也适合小白学习进阶,当然也可作为毕设项目、课程设计、作业、项目初期立项演示等。
3、如果基础还行,也可在此代码基础上进行修改,以实现其他功能,也可用于毕设、课设、作业等。
下载后请首先打开README.md文件(如有),仅供学习参考, 切勿用于商业用途。