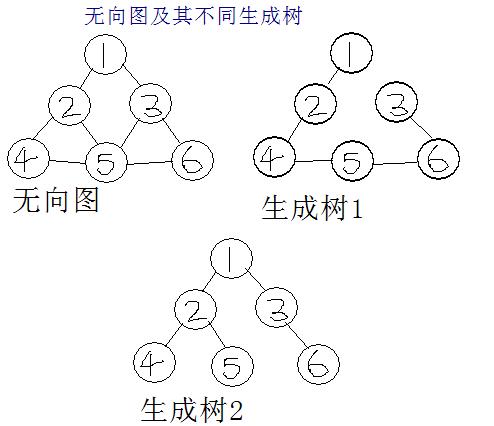
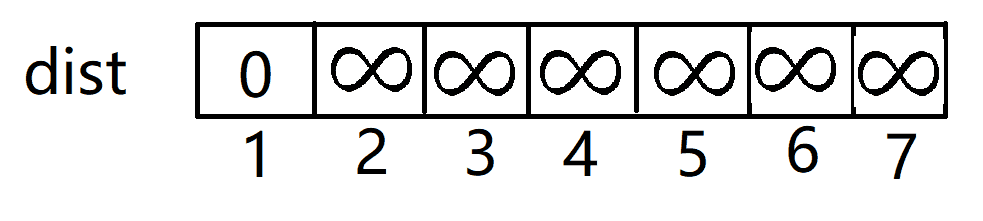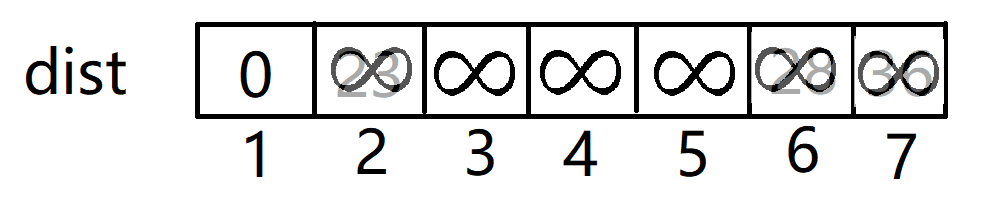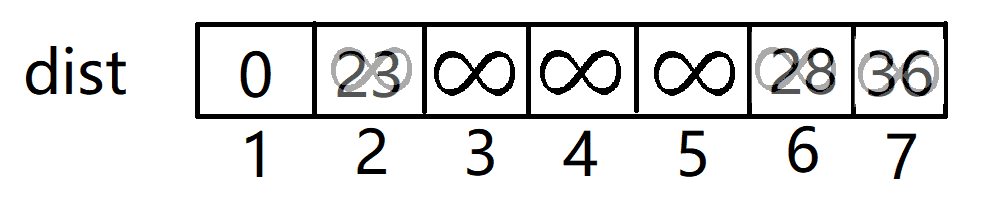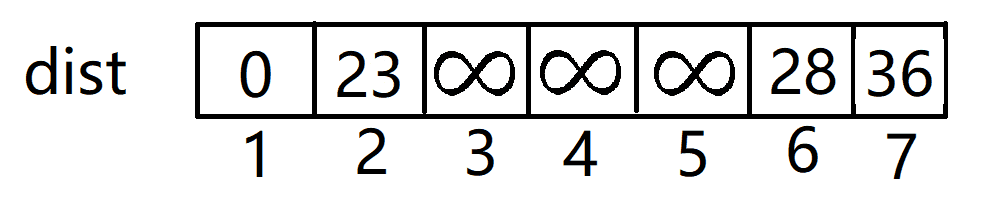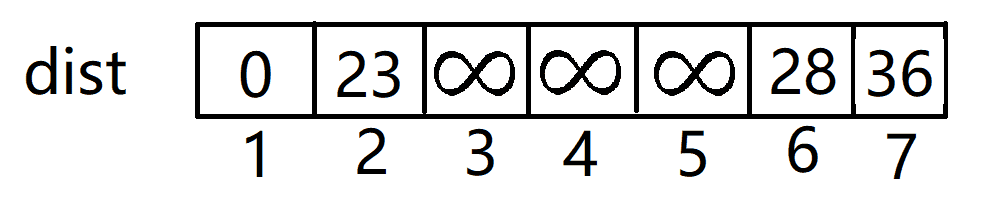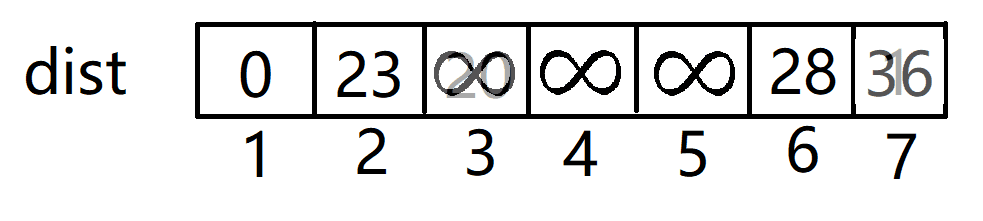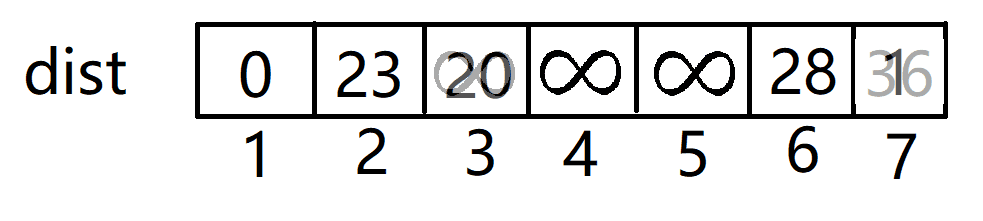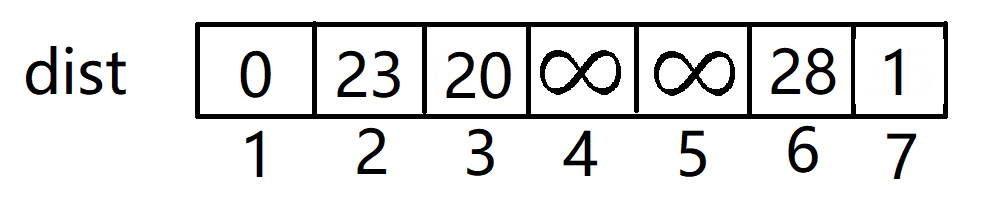最小生成树的概念
在一给定的无向图G = (V, E) 中,(u, v) 代表连接顶点 u 与顶点 v 的边,而 w(u, v) 代表此的边权重,若存在 T 为 E 的子集(即)且为无循环图,使得的 w(T) 最小,则此 T 为 G 的最小生成树。最小生成树其实是最小权重生成树的简称。(简而言之就是把一个图变成一棵树,并且树中的边权和最小)
经典题目
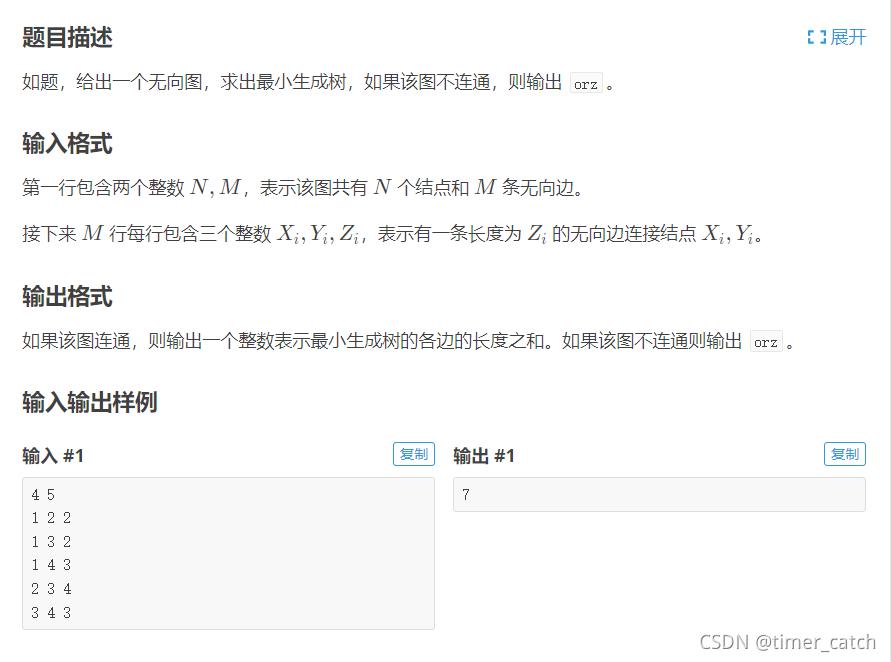
P3366 【模板】最小生成树 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
(这道题的数据过大,为了简化问题,我们假定数据范围可以用一个二维数组存下)
prim算法简介
prim算法基于贪心,我们每次总是选出一个离生成树距离最小的点去加入生成树,最后实现最小生成树(不做证明,理解思想即可)
prim算法解析 (详细图解)
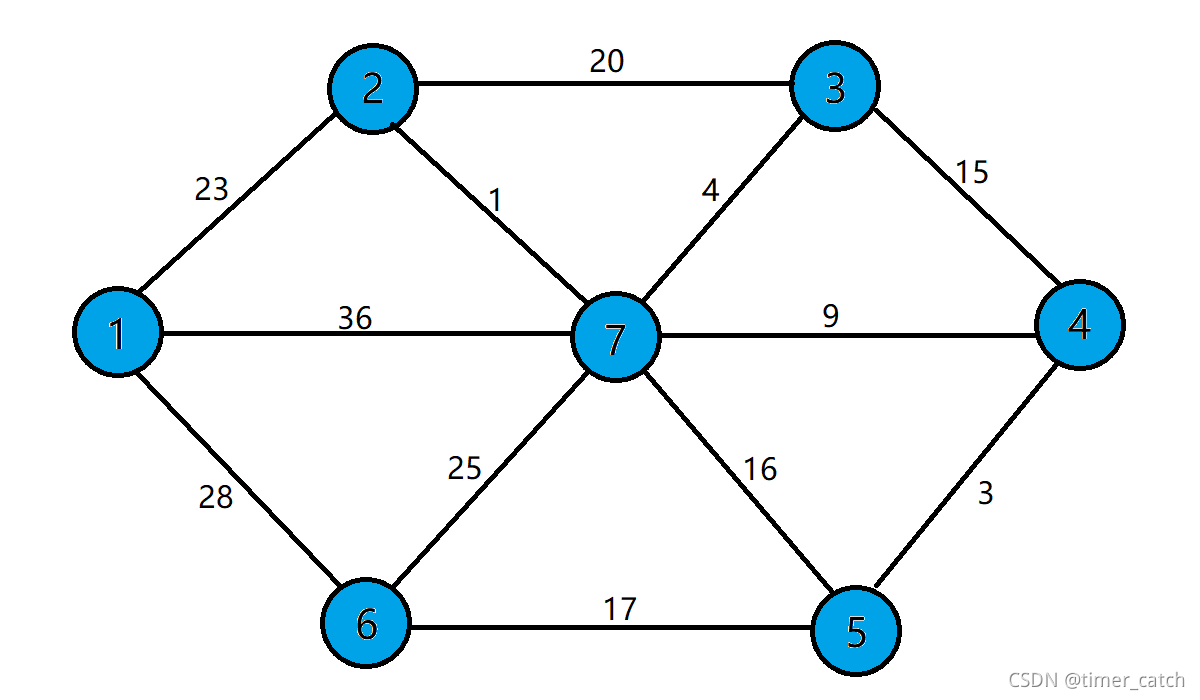
(随机构建一个无向图)
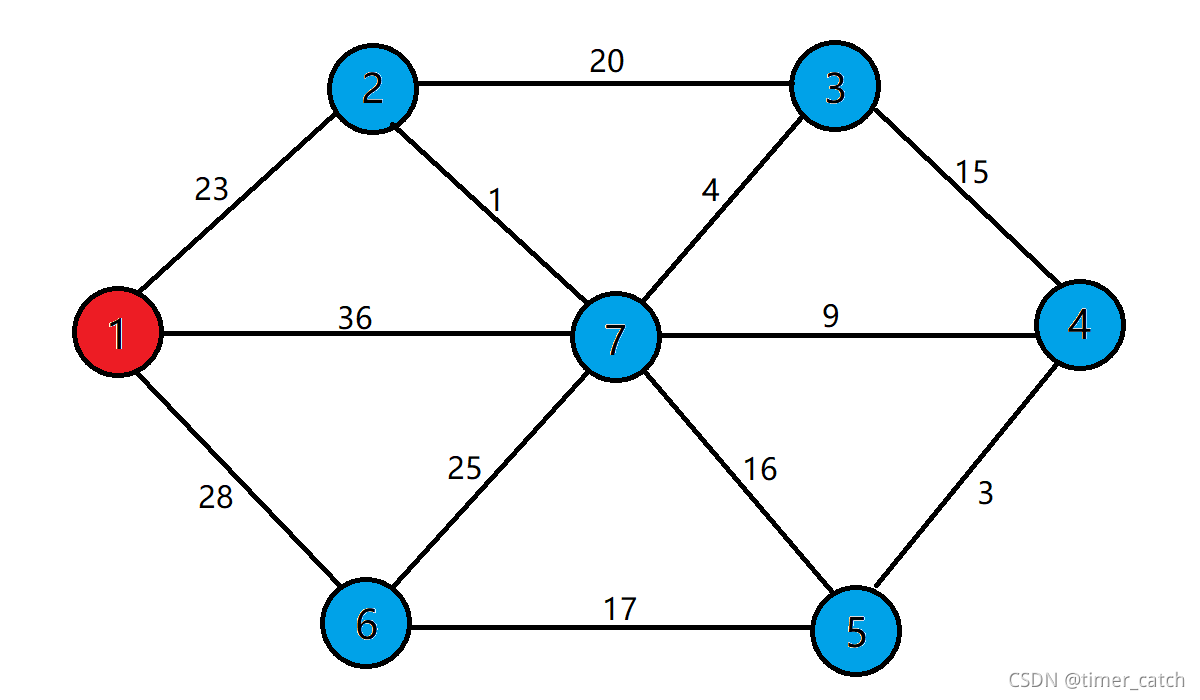
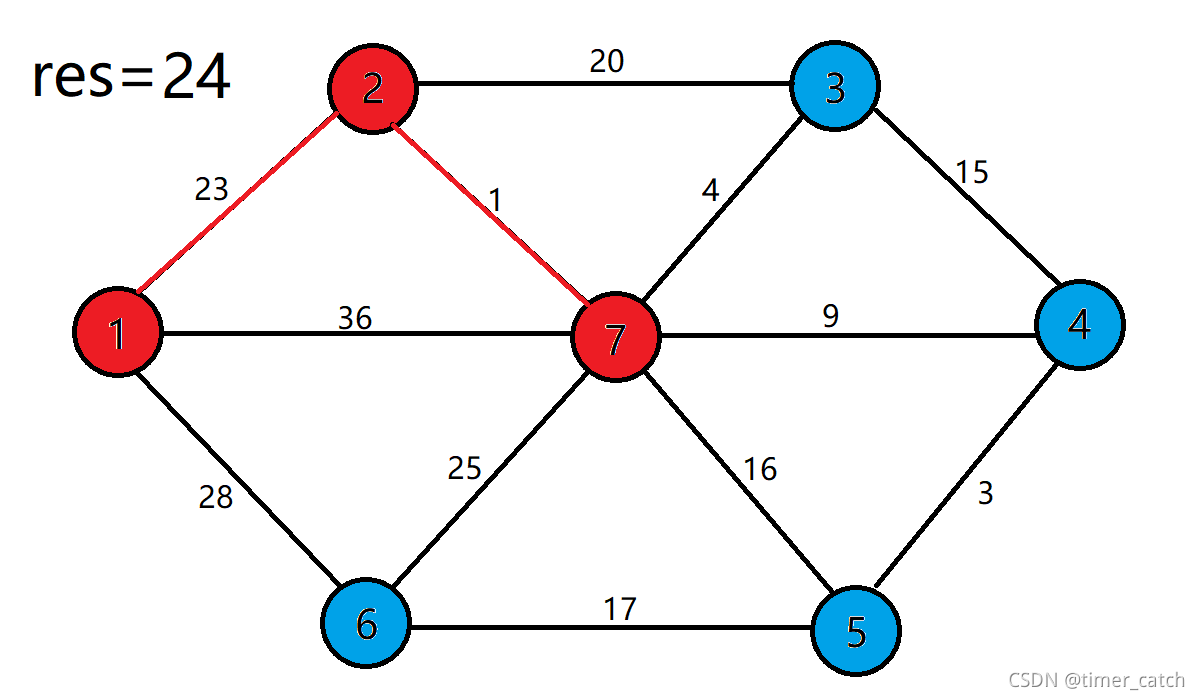
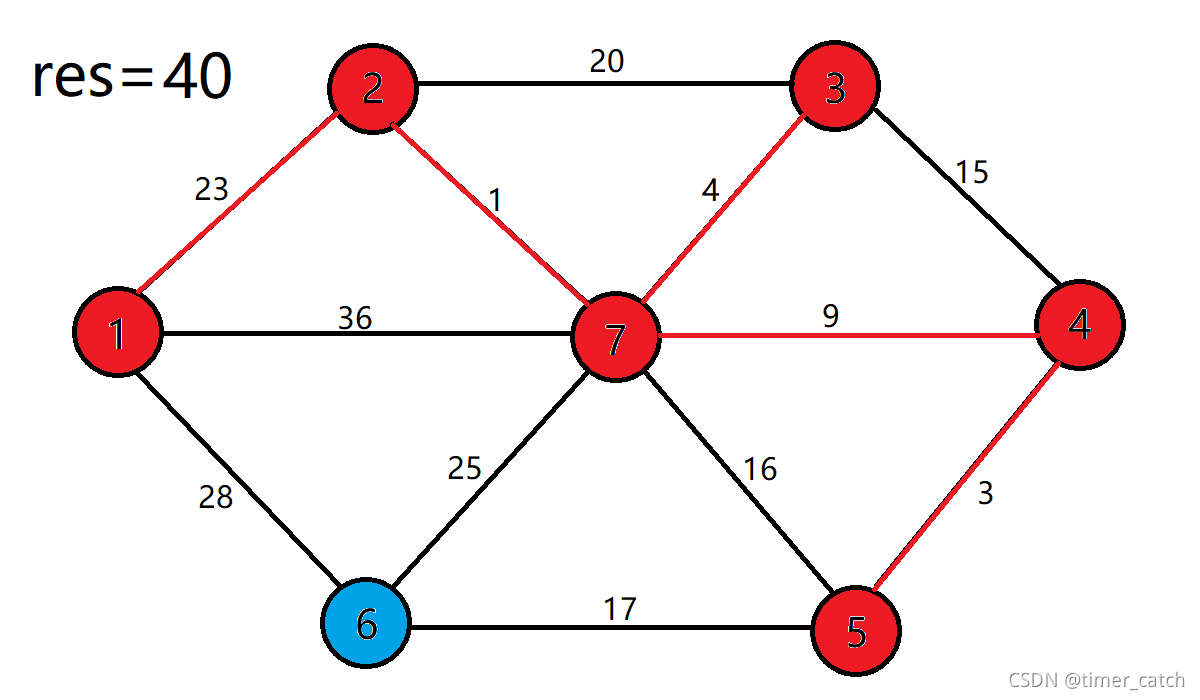
- 现在我们构建两个集合S(红色的点),V(蓝色的点),S集合中存放的是已近加入最小生成树的点,V集合中存放的是还没有加入最小生成树的点。显然刚开始时所有的点都在V集合中。
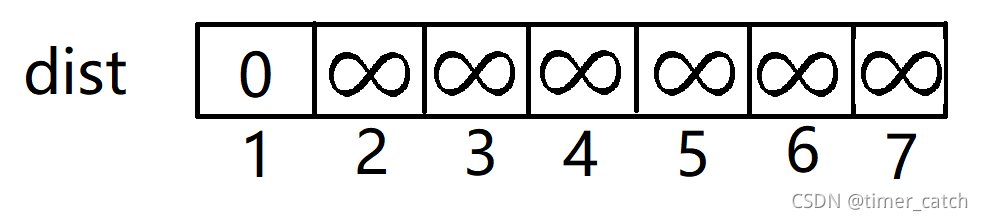
- 然后们先将任意一个点加入集合S中(默认为点1),并且初始化所有点(除了点1)到集合S的距离是无穷大。
- 用一个变量res存放最小生成树所有边权值的和。我们每次都选择离S集合最近的点加入S集合中,并且用新加入的点去更新dist数组,因为只有一个新的点加入到集合S中,到集合S的距离才有可能更新(贪心,每次都选最小的)。
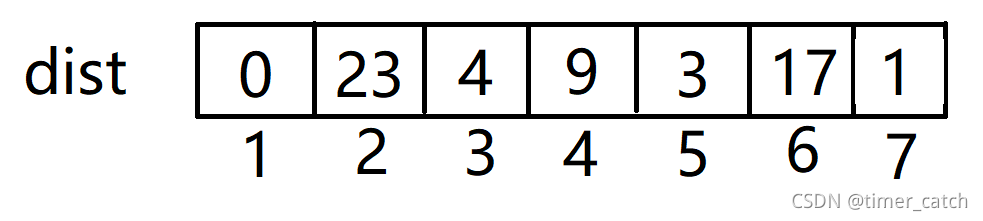
- 更新就是看一下能否通过新加入的点使到达集合的距离变小(看下面dist数组的变化)。
- 我们开始在加入点1后开始第一次更新。
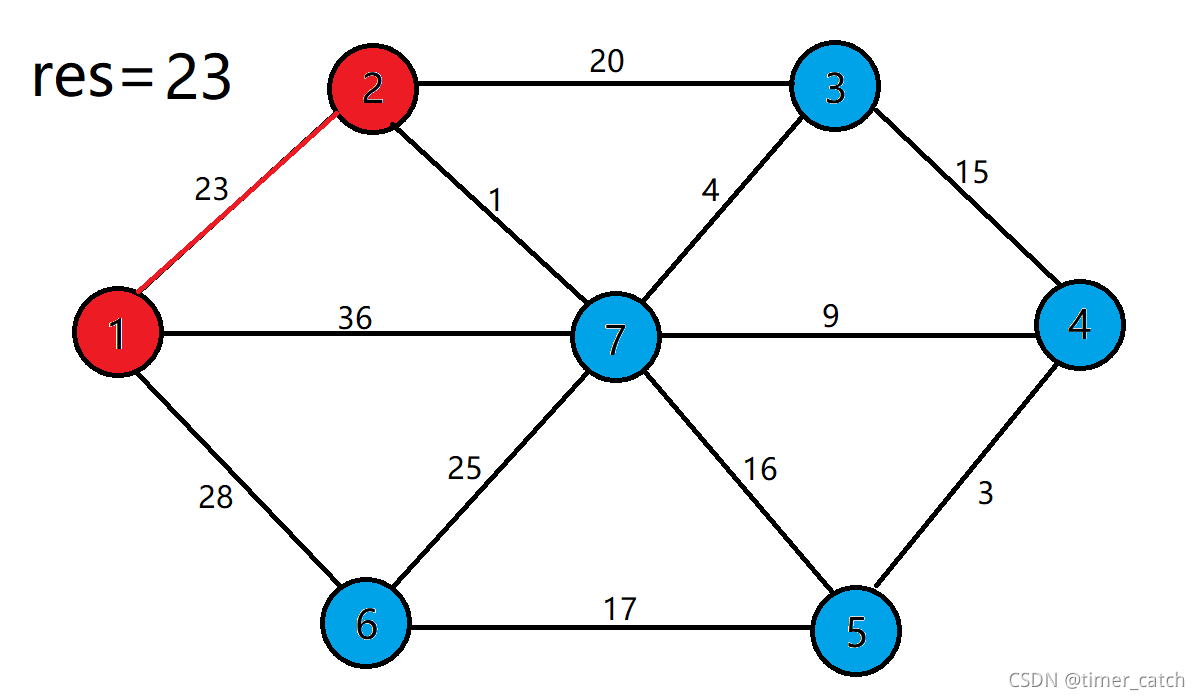
- 现在集合S={1},集合V={2,3,4,5,6,7},根据贪心策略,我们选择离集合S最近的点加入 ,即点2,并把这一条边的权值加到res中。
- 集合更新为S={1,2},V={3,4,5,6,7},并用点2去更新dist数组,我们发现点3和点7都可以都可以通过边2-3,2-7缩短到集合S得距离。
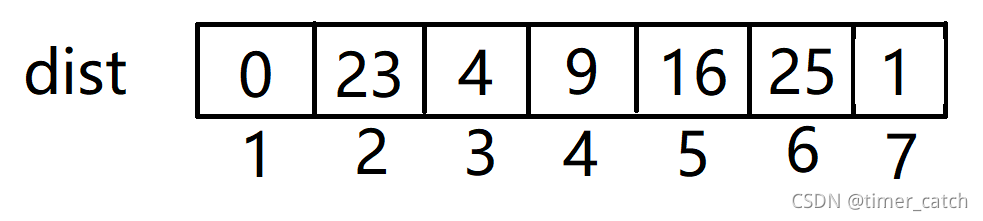
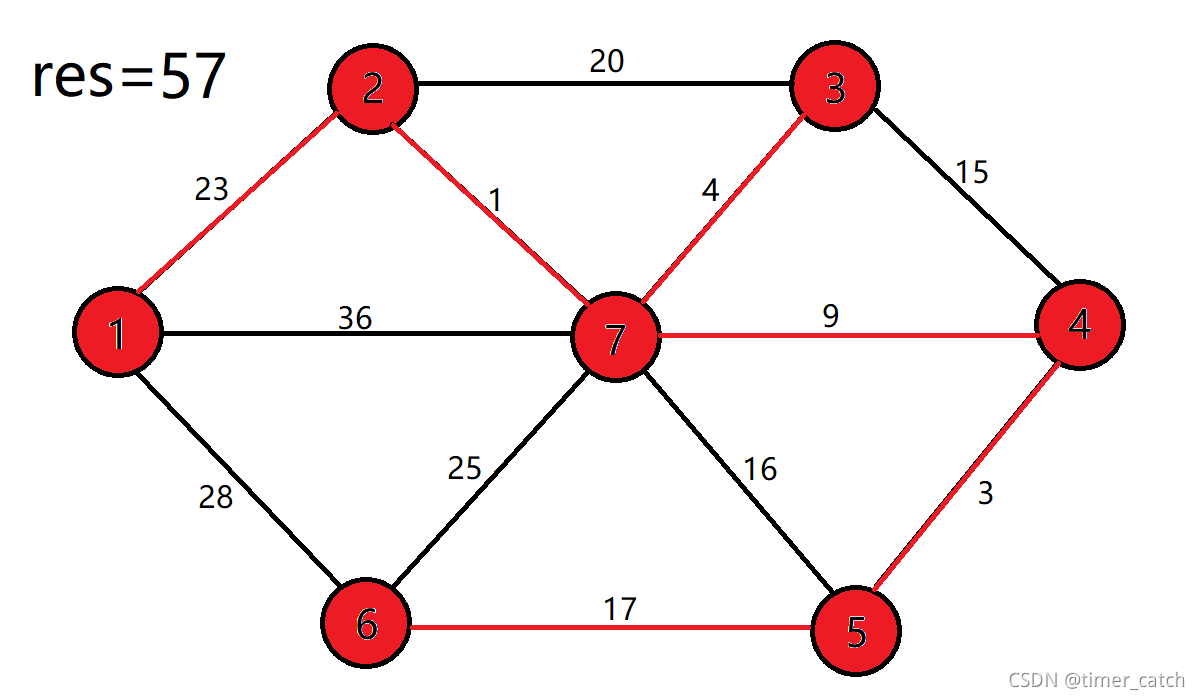
- 重复上面的步骤,直到将全部的点加入到最小生成树中。
- 3并不能更新任何点
- 这样一颗最小生成树就构建完成了,权值和是57。
代码实现
-
const
int MAXN =
1000,INF =
0x3f3f3f3f;
//定义一个INF表示无穷大。
-
int g[MAXN][MAXN],dist[MAXN],n,m,res;
-
//我们用g[][]数组存储这个图,dist[]储存到集合S的距离,res保存结果。
-
bool book[MAXN];
//用book数组记录某个点是否加入到集合S中。
-
int main()
-
{
-
cin>>n>>m;
//读入这个图的点数n和边数m
-
for(
int i =
1 ; i<= n ;i++)
-
{
-
for(
int j =
1; j <= n ;j++)
-
{
-
g[i][j] = INF;
//初始化任意两个点之间的距离为正无穷(表示这两个点之间没有边)
-
}
-
dist[i] = INF;
//初始化所有点到集合S的距离都是正无穷
-
}
-
for(
int i =
1; i <= m ; i++)
-
{
-
int a,b,w;
-
cin>>a>>b>>w;
//读入a,b两个点之间的边
-
g[a][b] = g[b][a] = w;
//由于是无向边,我们对g[a][b]和g[b][a]都要赋值
-
}
-
prim();
//调用prim函数
-
if(res==INF)
//如果res的值是正无穷,表示不能该图不能转化成一棵树,输出orz
-
cout<<
"orz";
-
else
-
cout<<res;
//否则就输出结果res
-
return
0;
-
}
-
void prim()
-
{
-
dist[
1] =
0;
//把点1加入集合S,点1在集合S中,将它到集合的距离初始化为0
-
book[
1] =
true;
//表示点1已经加入到了S集合中
-
for(
int i =
2 ; i <= n ;i++)dist[i] =
min(dist[i],g[
1][i]);
//用点1去更新dist[]
-
for(
int i =
2 ; i <= n ; i++)
-
{
-
int temp = INF;
//初始化距离
-
int t =
-1;
//接下来去寻找离集合S最近的点加入到集合中,用t记录这个点的下标。
-
for(
int j =
2 ; j <= n; j++)
-
{
-
if(!book[j]&&dist[j]<temp)
//如果这个点没有加入集合S,而且这个点到集合的距离小于temp就将下标赋给t
-
{
-
temp = dist[j];
//更新集合V到集合S的最小值
-
t = j;
//把点赋给t
-
}
-
}
-
if(t==
-1){res = INF ;
return ;}
-
//如果t==-1,意味着在集合V找不到边连向集合S,生成树构建失败,将res赋值正无穷表示构建失败,结束函数
-
book[t] =
true;
//如果找到了这个点,就把它加入集合S
-
res+=dist[t];
//加上这个点到集合S的距离
-
for(
int j =
2 ; j <= n ; j++)dist[j] =
min(dist[j],g[t][j]);
//用新加入的点更新dist[]
-
}
-
}
代码实战
纸上得来终觉浅,绝知此事要躬行,也许看完了上面的解析,你已经最prim算法有了一个大致的了解,学习算法,大致的了解是远远不够的,代码的实践永远是最重要的,学习完一个算法后一定要去自己亲手试试,每个人都有自己的代码风格,大家大可以在自己的风格之上写出自己的prim。
| prim习题 | 简介 | 难度 |
|---|---|---|
| P3366 【模板】最小生成树 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) | 模板题 | ★☆☆☆☆ |
| P1967 [NOIP2013 提高组] 货车运输 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) | 基本应用 | ★☆☆☆☆ |
| P1991 无线通讯网 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) | 基本应用 | ★☆☆☆☆ |
第一题是模板,后面两题主要是更好得帮助我们理解最小生成树——prim在实际和题目中得应用。