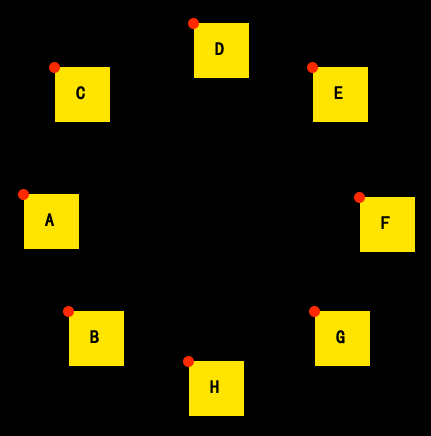
效果图:
一、分析图:
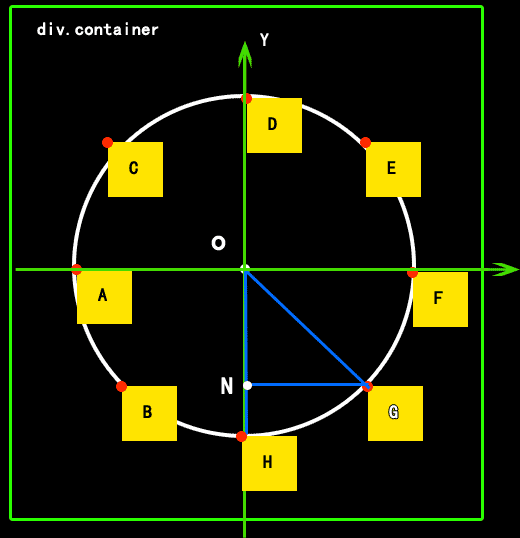
绿色边框内:外层的DIV元素,相对定位;
白色圆形框:辅助分析的想象形状;
白点:为白色圆形的圆心点,中心点,点o;
圆心角:角NOG;
黄色:需要按圆形排列的,绝对定位的DIV元素;
红色点:为每个黄色DIV的坐标点;即绝对定位时的元素,left值 和 top值 ,设置的点;
二、涉及到的概念定义:
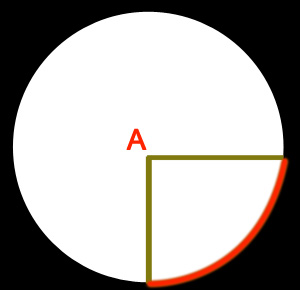
2.1、弧度:弧度是角的度量单位。
(红色部分为弧长,角A为弧长对应的圆心角)
弧长等于半径的弧,其所对的圆心角为1弧度。(即两条射线从圆心向圆周射出,形成一个夹角和夹角正对的一段弧。当这段弧长正好等于圆的半径时,两条射线的夹角的弧度为1)。
根据定义,一周的弧度数为2πr/r=2π,360°角=2π弧度,因此,1弧度约为57.3°,即57°17'44.806'',1°为π/180弧度,近似值为0.01745弧度,周角为2π弧度,平角(即180°角)为π弧度,直角为π/2弧度。
弧长=n2πr/360 (在这里n就是角度数,即圆心角n所对应的弧长。)
========================================================
2.2、正弦值:弦值是在直角三角形中,对边的长比上斜边的长的值。
Math.sin(x) : X 必需。一个以弧度表示的角。将角度乘以 0.017453293 (2PI/360)即可转换为弧度。
================================================
2.3、余弦值:是指直角三角形锐角邻边与斜边的比值。
Math.sin(x) : X 必需。一个以弧度表示的角。将角度乘以 0.017453293 (2PI/360)即可转换为弧度。
三、需求分析:
3.1 让这些黄色的DIV ,在同一个圆的圆周上排列
3.2 排列的方式是平均分布
四、原理分析:
要让DIV的排列,形成一个圆形,实质就是设置每个DIV的left值 和 TOP值 之间的关系,让它们之间值的关系,按照圆形的规律去设值;
4.1 圆形的规律是什么?
是PI(圆周率); 任何值乘以这个PI再乘2,就可以得到一个圆形。这个“任何值”就是得到的圆形的半径;值越大,当然这个圆形也就越大。
4.2 怎么找到每个DIV的Left 和 TOP值之关系?
上图中的每个黄色DIV左上角的红色点的坐标,就是left 和 TOP值 ,要让这个红色的点,正好分布在这个圆周上面,那么Left 和 top 必然要和这个PI关联起来。有PI才有圆。
五、实例分析
我要得到上图中,红点的坐标值,即DIV的left 和 TOP值,
LEFT = NG + o的横坐标值(left)
TOP = ON + or的纵坐标值(TOP)
所以先要求出每个一以圆心o为顶点,以圆形半径为斜边,的直角三角形的两个直角边的值。(上图中蓝色直角三角形的ON线段和NG线段的长度值)
以半边圆形来看,当圆心角变大,半径不变的情况下,这个底边的值,是会变大的;
正弦公式:sin(X) = 对边/斜边 X变大,斜边不变(半径),那么对边(上图中的NG线段)是会变大的;
余统公式 cos(X) = 邻边/斜边 X变大,斜边不变(半径),那么邻边(上图中ON线段) 是会变小的;
270度的正统值,是负1;
180的余弦值是,是负1;
5.1 先设定一个圆
半径:200px;
5.2 平均这个圆的圆周
假设我们有8个DIV 要平均分布在这个半径为200PX的圆周上面。那么这里我们通过角度去平均(弧线的划分也好,平均也好,冒似都应该通过角度去划分);
平均:圆形的圆心角的总角度为360度,平均成8份,就是360/8; 这样平分后的每一个圆心角,所对的弧长,弧度,就都是相等的。
5.3 求出NG的长度值,也就是DIV的left值,即红点的横坐标值;
求这个值,要用到正弦函数;
公式 Math.sin(X) = 对边/斜边;
我们需要知道X,需要知到斜边;就可以求出“对边”值,即NG的长度值;
5.3.1 这里的X是弧度,即角度数;上面定义中说过,弧度数是表示角度数的;
根据公式: 角度数乘以 PI/180,就是弧度数; 即 X = (360/8)* PI/180
这个求出的X就是把圆形平分之后,的弧度数;
5.3.2 斜边,就是这个圆形的半径,即 200;
5.3.3 “对边”值,即NG的长度值;
根据上面的公式变形:对边(NG ) = Math.sin(X)*斜边
即 :对边(NG )= Math.sin(X)* 200 = Math.sin( (360/8)* PI/180 )* 200;
好了,现在把对边(NG )的值求出来了;也就是红点的横坐标值,即DVI的LEFT值;
5.4 求出每一个圆心角对应的直角边,即对边的长度值
因为每一个圆心角,都是均分的,所以乘以一个倍数,就得到不周圆心角对应的弧度值,即角度值
这里用DIV的索引为倍数,值乘以X,就得到每个均分后,每个圆心角的弧度值;
对边 = Math.sin(X*索引)* 200;
用这个求出的【对边】值 做为DIV的left值;
5.5 DIV的TOP值,即ON线段的长度值
以上面四点的原理一样,只不过把正弦值,改为余弦值
邻边(ON) = Math.COS(X*索引)* 200;
把这个值设为 DIV的TOP值;
根据以上分析:代码如下,就可以按一个圆形,来排列DIV
//半径 var radius = 200; //每一个BOX对应的角度; var avd = 360/$(".box").length; //每一个BOX对应的弧度; var ahd = avd*Math.PI/180; $(".box").each(function(index, element){ $(this).css({"left":Math.sin((ahd*index))*radius,"top":Math.cos((ahd*index))*radius}); });
5.6 设置这个圆形的位置
圆形的位置,是根据这个圆形的圆心坐标来定的,所以我们就是要设置,圆心的坐标值,left top
圆心的坐标坐变化了,那么对应DIV的left top也应该改变;
比如圆心的left :100PX ; TOP:100px;
那么每个DIV的LEFT和TOP也应该加上这个值:
代码如下
$(function(){ //中心点横坐标 var dotLeft = ($(".container").width()-$(".dot").width())/2; //中心点纵坐标 var dotTop = ($(".container").height()-$(".dot").height())/2; //起始角度 var stard = 0; //半径 var radius = 200; //每一个BOX对应的角度; var avd = 360/$(".box").length; //每一个BOX对应的弧度; var ahd = avd*Math.PI/180; //设置圆的中心点的位置 $(".dot").css({"left":dotLeft,"top":dotTop}); $(".box").each(function(index, element){ $(this).css({"left":Math.sin((ahd*index))*radius+dotLeft,"top":Math.cos((ahd*index))*radius+dotTop}); }); })
六 总结:
6.1 在涉及到曲线或弧线的时候,应该用角度或弧度去分析,找关联;
6.2 找关系或比例,让值和值之间是一个关系式,会用到乘以或除以一个倍数;( 例如以前写过的放大镜,就是用比例关系);
七 先前的理解有误,现在更新了分析的图片和分析;感谢 “ 弦”!的提示~