冒泡排序：（稳定）

1.   比较相邻的元素。如果第一个比第二个大，就交换他们两个。

2.   对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。

3.   针对所有的元素重复以上的步骤，除了最后一个。

4.    持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

选择排序：

1.   首先，找到数组中最小的那个元素，

2.   其次，将它和数组的第一个元素交换位置(如果第一个元素就是最小元素那么它就和自己交换)。

3.   再次，在剩下的元素中找到最小的元素，将它与数组的第二个元素交换位置。

4.    如此往复、直到将整个数组排序.这种方法叫做选择排序，因为它在不断地选择剩余元素之中的最小者。

不稳定：举个例子，序列5 8 52 9， 我们知道第一遍选择第1个元素5会和2交换，那么原序列中2个5的相对前后顺序就被破坏了，所以选择排序不是一个稳定的排序算法

插入排序：（稳定）

从第个位置的元素开始，若相邻元素，则交换；否则进行第个位置的元素的插入排序；适用于前期较有序的序列

Shell排序：（不稳定）

相对于插入排序相邻变为相差：从第个位置的元素开始，若，则交换；否则进行第个位置的元素的插入排序；排完当前后，，继续排序。（到最后都会回归到（插入排序），但是前期的排序为插入排序提供了良好的基础）

归并排序:

基本思想： 嵌套循环

自顶向下：尺寸由大到小切割排序，再合并；

自底向上：尺寸小到大排序，再合并；

快速排序：

选择一个元素将所有大于该元素的元素放在右边，所有小于该元素的元素放到左边；再对左序列和右序列分别进行快速排序，直到子序列的长度为1。

堆排序：

基于二叉树，每次排序成大顶堆二叉树（每个结点的值都大于或等于其左右孩子结点的值），最后一个叶节点的值为最小值，一次排序直到依次找出所有排序过程中的最小值。

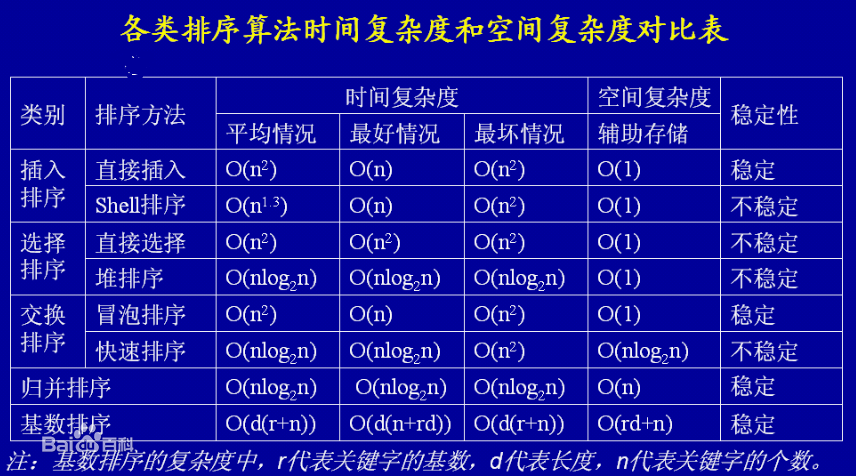
图片来源：

https://baike.baidu.com/pic/%E6%97%B6%E9%97%B4%E5%A4%8D%E6%9D%82%E5%BA%A6/1894057/0/b999a9014c086e06b5dc7f6d00087bf40ad1cba4?fr=lemma&ct=single#aid=0&pic=b999a9014c086e06b5dc7f6d00087bf40ad1cba4