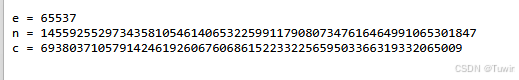easyrsa1
题目:
对比发现其实这里的n并不大(和后面的题目对比),所以可以直接分解n
分解n几种方式:
1、在线网站
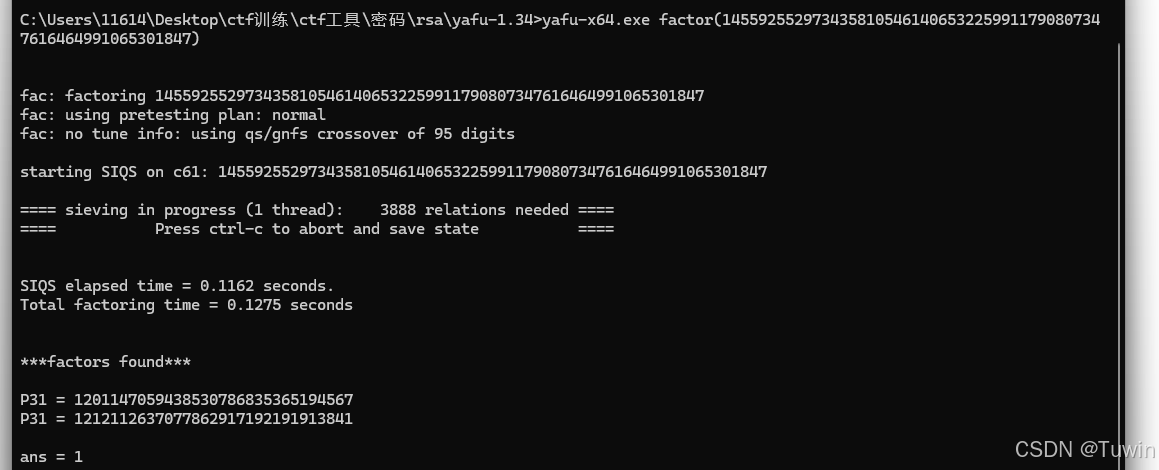
2、yafu工具分解
yafu-x64.exe factor(要分解的质数)
3、对于相近的 p p p和 q q q可以使用费马分解
这里出来
p
=
1201147059438530786835365194567
p=1201147059438530786835365194567
p=1201147059438530786835365194567
q
=
1212112637077862917192191913841
q=1212112637077862917192191913841
q=1212112637077862917192191913841
所以
ϕ
(
n
)
=
(
p
−
1
)
(
q
−
1
)
=
1455925529734358105461406532257498531110831222760963508193440
\phi(n)=(p-1)(q-1)=1455925529734358105461406532257498531110831222760963508193440
ϕ(n)=(p−1)(q−1)=1455925529734358105461406532257498531110831222760963508193440
d
=
ϕ
(
n
)
/
/
e
=
22215321570019349458495300856882349376853246605138524927
d=\phi(n) //e=22215321570019349458495300856882349376853246605138524927
d=ϕ(n)//e=22215321570019349458495300856882349376853246605138524927
m
=
c
d
=
584734024210318745406046669953309948776602881661
m=c^{d}=584734024210318745406046669953309948776602881661
m=cd=584734024210318745406046669953309948776602881661
这里根据rsa加解密算法写个简单的解密脚本
import gmpy2
import binascii
e = 65537
n = 1455925529734358105461406532259911790807347616464991065301847
p = 1201147059438530786835365194567
q = 1212112637077862917192191913841
c = 69380371057914246192606760686152233225659503366319332065009
phi_n = (p-1)*(q-1)
d = gmpy2.invert(e,phi_n)
m = gmpy2.powmod(c, d, n)
print(m)
print(binascii.unhexlify(hex(m)[2:]))