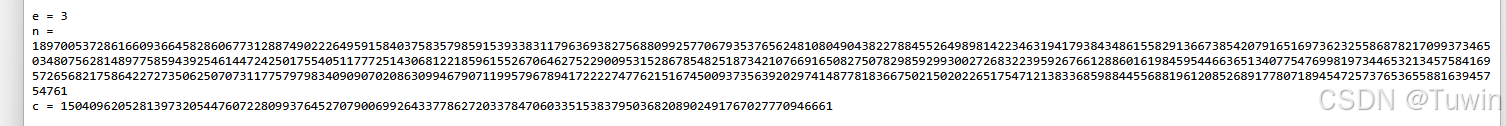ctfshow easyrsa4 低指爆破

题目

其中e很小
推导
$c\equiv m^e\mathrm{mod}n\equiv c+k\ast n$这里的k是一个整数
=>那么$m\equiv (c+k\ast n{)}^{1/e}\mathrm{mod}n$
所以代码如下：

import gmpy2
import binascii

e = 3
n = 18970053728616609366458286067731288749022264959158403758357985915393383117963693827568809925770679353765624810804904382278845526498981422346319417938434861558291366738542079165169736232558687821709937346503480756281489775859439254614472425017554051177725143068122185961552670646275229009531528678548251873421076691650827507829859299300272683223959267661288601619845954466365134077547699819734465321345758416957265682175864227273506250707311775797983409090702086309946790711995796789417222274776215167450093735639202974148778183667502150202265175471213833685988445568819612085268917780718945472573765365588163945754761
c = 150409620528139732054476072280993764527079006992643377862720337847060335153837950368208902491767027770946661

i = 0
while True:
	if gmpy2.iroot((c+i*n),3)[1] == True:#iroot(x,n)对x开n次方，返回整数和布尔值（能被完全开方为整数，则返回True；不能，则返回False）
			m = gmpy2.iroot((c+i*n),3)[0]
			break
	i +=1
print(binascii.unhexlify(hex(m)[2:]))