01背包模板

01背包：每个物品 要和不要 两种可能性展开

题目链接

01背包_洛谷

01背包模板解释

01背包：每个物品选择要还是不要
每个物品有自己的体积和价值
定义一张dp表=》二维表
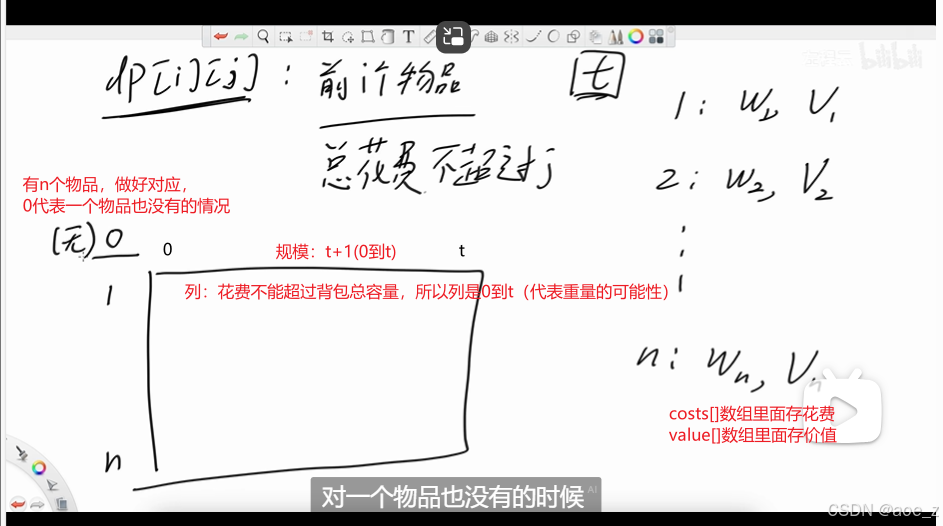
dp[i][j]代表：前i个物品：在整个的容量不超过j的情况下，能获得的最大价值是多少
如图解释：

那么如何把这张表填好呢？
对于dp的定义是：（自由选择）前i个物品，总花费不超过j的情况下最好的价值，那么这个对应的就是二维表里面最右下角的格子。
最右下角的格子代表什么：
前n个物品，在总容量不超过t的情况下，所获得的最好价值（如上图）。所以我们只要想办法把二维表填好，那么最右下角的值就是最终想要的结论。
dp如何转移
①不要i号物品：如果1到i上面的物品自由选择，此时你又决定不要i号物品时，那么dp[i][j]其实就是dp[i-1][j]。不要i号物品，那么1到i的选择和1到i-1的选择是一样的。
②要i号物品：要i号物品的话，要加上它的价值val[i]，你1到i号物品中选择，要求它们容量不要超过j，而现在选择了i号物品，所以要去掉i号物品的体积，所以i-1那些物品的容量限制是j-cost[i]。dp[i-1][j-cost[i]]。
图示：
注意：
第二种选择中，有可能j-cost[i]为负数。
以上就是转移方程的得出
通过转移方程，就知道如何填格子了，在二维dp表中来到i行，背包限制是j，那这个格子填的方法就是dp[i][j]，
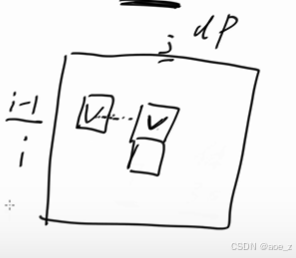
第一种情况：依赖上面的格子
第二种可能：依赖上一行的某个格子
如图

所以二维表如何填？
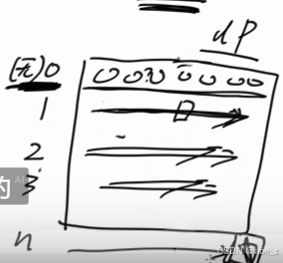
把第零行（一个物品也没有的情况下都填好初始值）然后来到第一行就可以从左向右依次填了…一直填到最后一个格子。
那么初始位置如何设置呢
即：一个物品也也没有的时候：就是dp0行的含义。
一个物品也没有，所以它的最大价值是0。=》第零行的数值都是零，如图。

代码

1.转移方程+不做空间压缩的普通形式（代码中的输入输出格式可以参考这一篇：高效率的输入输出格式）

2.空间压缩
用一维数组代替二维数组
让一维数组不断地变为对应的二维数组的第零行，第一行…
然后我们又知道，这个格子的更新，
是依赖它的上面的一个格子，和左上角的一个格子来进行更新的（对应的想象二维数组）
所以让一维数组从右往左依次更新就行
即：推到每一个格子的时候，
在没有更新的之前，我的这个格子的内容就是我上方的值
为什么从右往左依次递推：从右向左的把这样行的值从第i行状况变为第i+1行状况
所以来到某个格子的时候，左边都是还没有更新的，（代表第i行的值）
更新后就代表第i+1行的dp值了
这样就可以用一个一维表代替一个二维表了

package class073;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.Arrays;

public class Code01_01Knapsack {

	public static int MAXM = 101;

	public static int MAXT = 1001;

	public static int[] cost = new int[MAXM];

	public static int[] val = new int[MAXM];

	public static int[] dp = new int[MAXT];

	public static int t, n;

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StreamTokenizer in = new StreamTokenizer(br);
		PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
		while (in.nextToken() != StreamTokenizer.TT_EOF) {
			t = (int) in.nval;
			in.nextToken();
			n = (int) in.nval;
			for (int i = 1; i <= n; i++) {
				in.nextToken();
				cost[i] = (int) in.nval;
				in.nextToken();
				val[i] = (int) in.nval;
			}
			out.println(compute2());
		}
		out.flush();
		out.close();
		br.close();
	}

	// 严格位置依赖的动态规划
	// n个物品编号1~n，第i号物品的花费cost[i]、价值val[i]
	// cost、val数组是全局变量，已经把数据读入了
	public static int compute1() {
//		第一行初始化为零，java设定数组初始化本来就是0，
//		所以就不用设置了
//		容量支持0到t，所以是长度是t+1
		int[][] dp = new int[n + 1][t + 1];
		for (int i = 1; i <= n; i++) {
			for (int j = 0; j <= t; j++) {
				// 不要i号物品
				dp[i][j] = dp[i - 1][j];
				if (j - cost[i] >= 0) {
					// 要i号物品
					dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - cost[i]] + val[i]);
				}
			}
		}
		return dp[n][t];
//		前n个物品，在容量不超过t的情况下，的最大价值
	}

//	 空间压缩
//	用一维数组代替二维数组
//	让一维数组不断地变为对应的二维数组的第零行，第一行......
//	然后我们又知道，这个格子的更新，
//	是依赖它的上面的一个格子，和左上角的一个格子来进行更新的（对应的想象二维数组）
//	所以让一维数组从右往左依次更新就行
//	即：推到每一个格子的时候，
//	在没有更新的之前，我的这个格子的内容就是我上方的值
//	为什么从右往左依次递推：从右向左的把这样行的值从第i行状况变为第i+1行状况
//	所以来到某个格子的时候，左边都是还没有更新的，（代表第i行的值）
//	更新后就代表第i+1行的dp值了
//	这样就可以用一个一维表代替一个二维表了
	public static int compute2() {
		Arrays.fill(dp, 0, t + 1, 0);
		for (int i = 1; i <= n; i++) {
			for (int j = t; j >= cost[i]; j--) {
				dp[j] = Math.max(dp[j], dp[j - cost[i]] + val[i]);
			}
		}
		return dp[t];
	}

}

总结

01背包模板+空间压缩优化
01背包模板