Bootstrap

剑指offer43-56树

剑指 Offer II 043. 往完全二叉树添加节点

在这里插入图片描述
在这里插入图片描述
完全二叉树除了最后一行都是满的

方法：层序遍历获取第一个不完整的节点

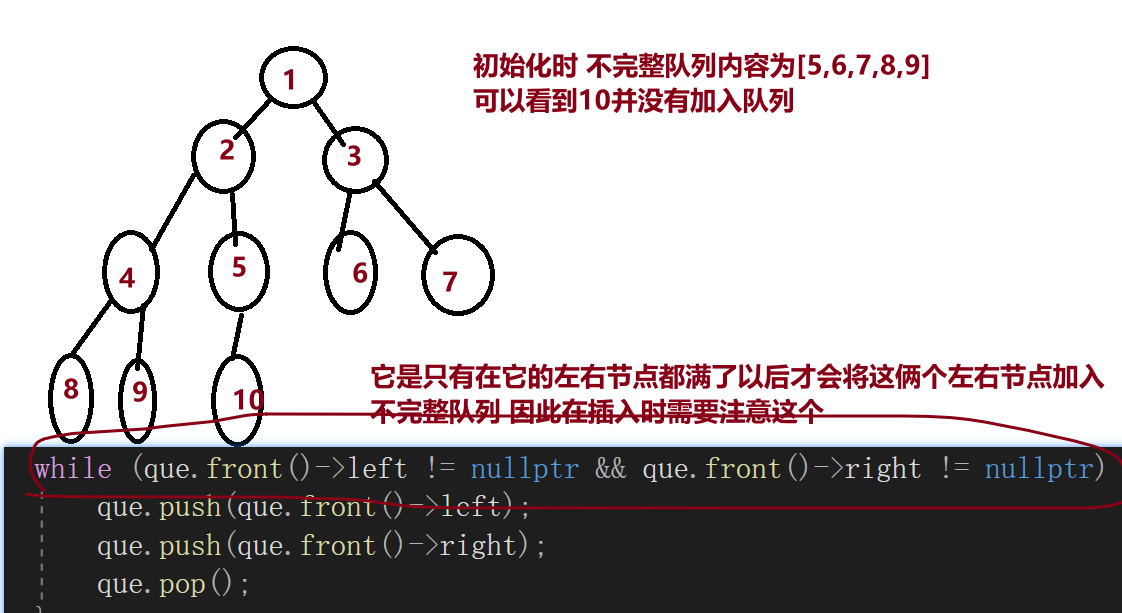
初始化时将不完整的节点加入到队列当中
插入时从队列找最先插入的节点，看它是左节点为空还是右节点为空，如果右节点为空说明父节点满了，就将父节点从不完整队列中弹出来，如果左节点为空，不做处理。最后将当前插入的节点加入到不完整队列中
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

代码

class CBTInserter {
private:
    queue<TreeNode*> que;
    TreeNode* root;
public:
    CBTInserter(TreeNode* root) {//初始化完全二叉树和不完整队列
        this->root = root;
        que.push(root);
        while (que.front()->left != nullptr && que.front()->right != nullptr) {
            que.push(que.front()->left);
            que.push(que.front()->right);
            que.pop();
        }
    }

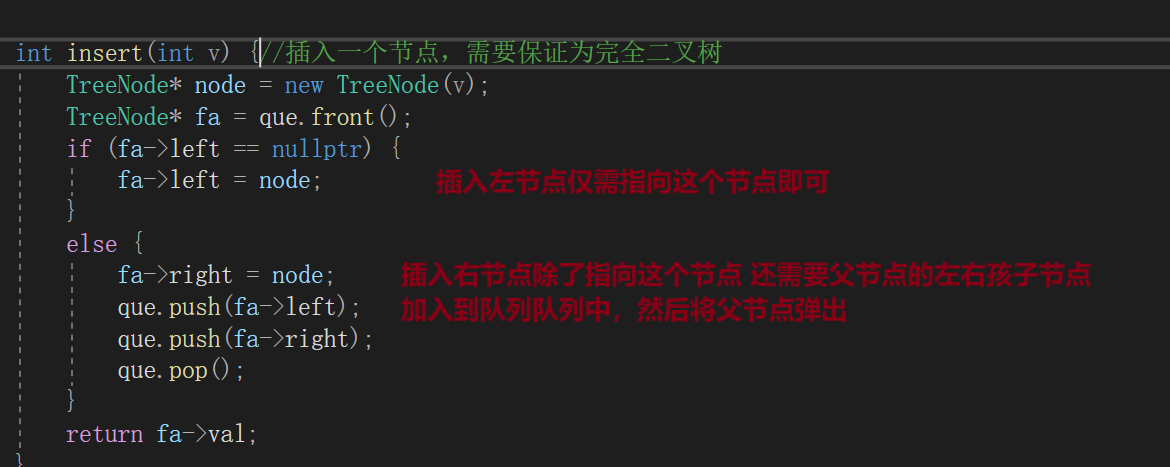
    int insert(int v) {//插入一个节点，需要保证为完全二叉树
        TreeNode* node = new TreeNode(v);
        TreeNode* fa = que.front();
        if (fa->left == nullptr) {
            fa->left = node;
        }
        else {
            fa->right = node;
            que.push(fa->left);
            que.push(fa->right);
            que.pop();
        }
        return fa->val;
    }

    TreeNode* get_root() { //获得输的根节点
        return this->root;
    }
};

剑指 Offer II 044. 二叉树每层的最大值

给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。
在这里插入图片描述
返回每层的最大值的节点

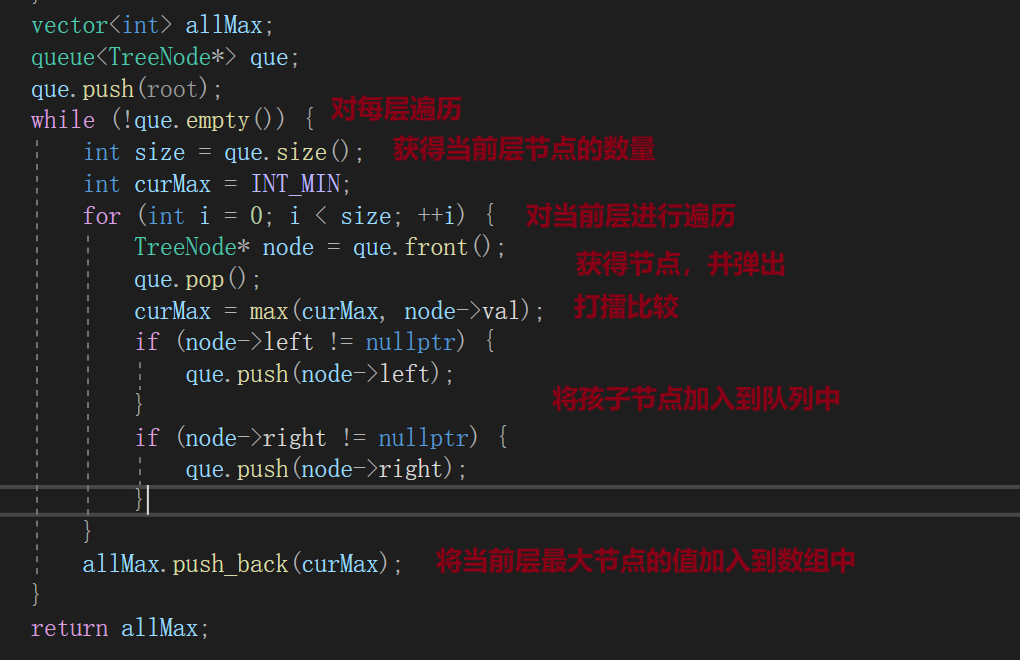
方法层次遍历，队列每次仅保存当前层的节点

在对每层进行遍历时，用队列.size()确定当前层的节点数量n，然后接一个for循环只处理n数量，将其加入孩子节点加入到队列中并求最大值
在这里插入图片描述

代码

class Solution {
public:
    vector<int> largestValues(TreeNode* root) {
        if (root == nullptr) {
            return {};
        }
        vector<int> allMax;
        queue<TreeNode*> que;
        que.push(root);
        while (!que.empty()) {
            int size = que.size();
            int curMax = INT_MIN;
            for (int i = 0; i < size; ++i) {
                TreeNode* node = que.front();
                que.pop();
                curMax = max(curMax, node->val);
                if (node->left != nullptr) {
                    que.push(node->left);
                }
                if (node->right != nullptr) {
                    que.push(node->right);
                }
            }
            allMax.push_back(curMax);
        }
        return allMax;
    }
};

剑指 Offer II 045. 二叉树最底层最左边的值

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。

假设二叉树中至少有一个节点。

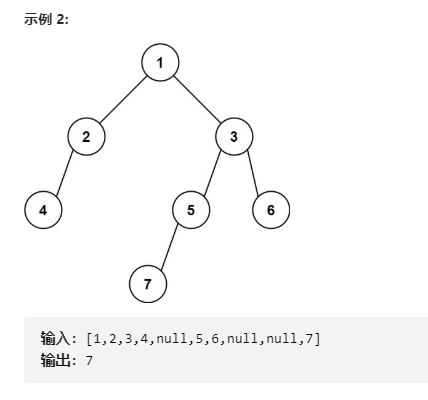
在这里插入图片描述
找最下面的最左边节点的值，比如上面那图的7

解法：层序遍历

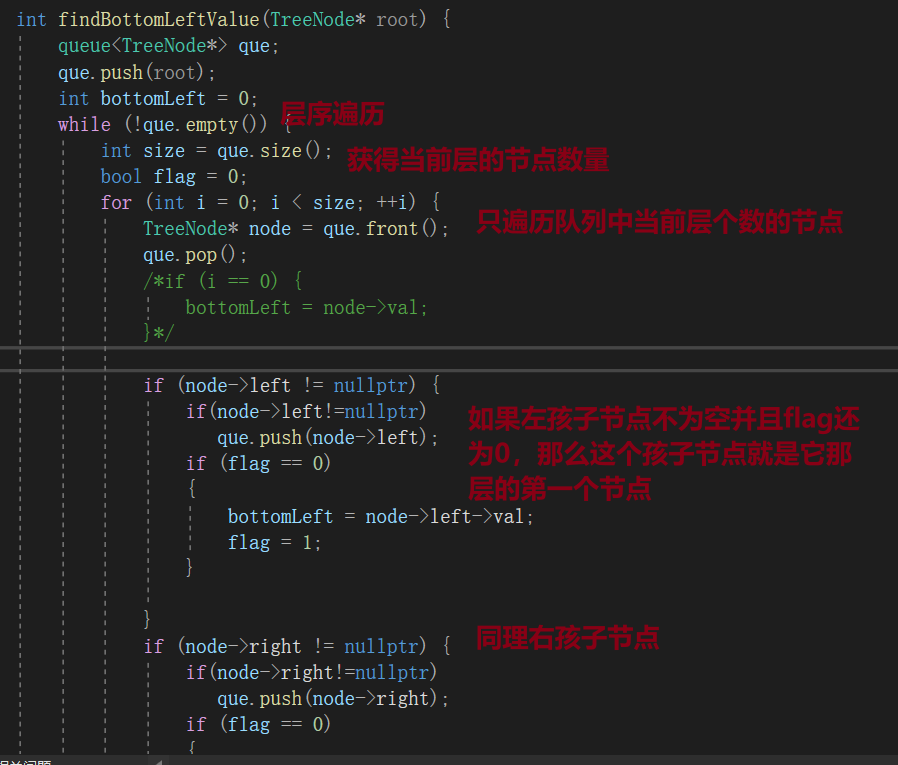
遍历每层时，用一个flag做标记，然后遍历每个节点的孩子节点，如果孩子节点并且flag未置1那么这个孩子节点就是它那一层的第一个节点。下面代码有点问题，将bottomLeft=0改为bottomeLeft=root->val;
在这里插入图片描述

代码

class Solution {
public:
    int findBottomLeftValue(TreeNode* root) {
          queue<TreeNode*> que;
        que.push(root);
        int bottomLeft = root->val;
        while (!que.empty()) {
            int size = que.size();
            bool flag = 0;
            for (int i = 0; i < size; ++i) {
                TreeNode* node = que.front();
                que.pop();
                /*if (i == 0) {
                    bottomLeft = node->val;
                }*/

                if (node->left != nullptr) {
                    if(node->left!=nullptr)
                       que.push(node->left);
                    if (flag == 0)
                    {
                        bottomLeft = node->left->val;
                        flag = 1;
                    }
                     
                }
                if (node->right != nullptr) {
                    if(node->right!=nullptr)
                       que.push(node->right);
                    if (flag == 0)
                    {
                        bottomLeft = node->right->val;
                        flag = 1;
                    }
                }
            }
        }
        return bottomLeft;
    }
};

剑指 Offer II 046. 二叉树的右侧视图

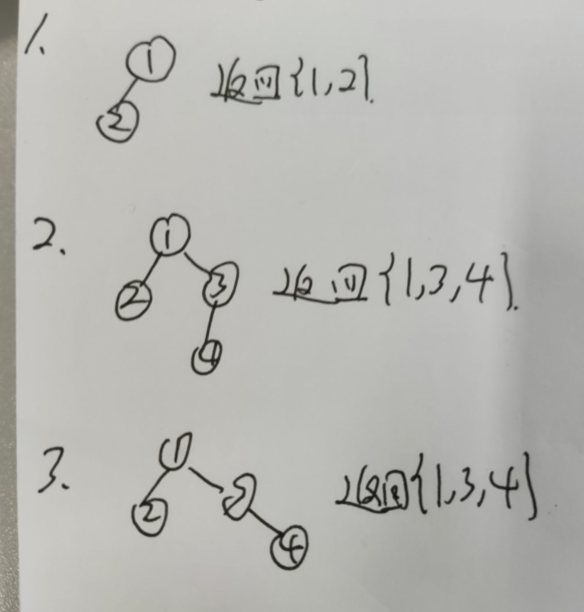
给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。
注意，并不是返回右节点的右节点，不可以只将右节点加入到里面，像下面第一个，返回的是1,2

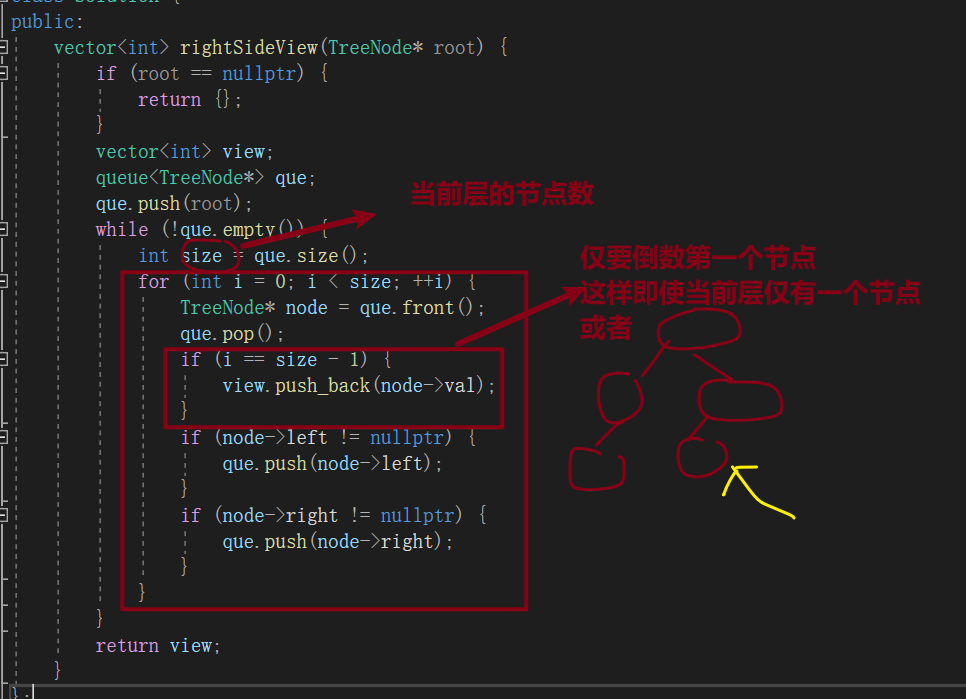
在这里插入图片描述

解法一：层序遍历

在这里插入图片描述

代码

class Solution {
public:
    vector<int> rightSideView(TreeNode* root) {
        if (root == nullptr) {
            return {};
        }
        vector<int> view;
        queue<TreeNode*> que;
        que.push(root);
        while (!que.empty()) {
            int size = que.size();
            for (int i = 0; i < size; ++i) {
                TreeNode* node = que.front();
                que.pop();
                if (i == size - 1) {
                    view.push_back(node->val);
                }
                if (node->left != nullptr) {
                    que.push(node->left);
                }
                if (node->right != nullptr) {
                    que.push(node->right);
                }
            }
        }
        return view;
    }
};

剑指 Offer II 047. 二叉树剪枝

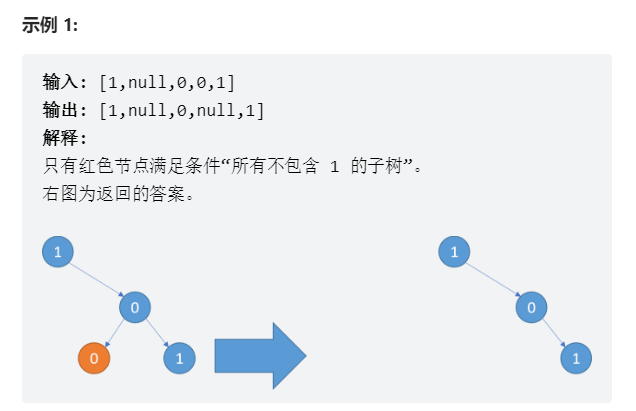
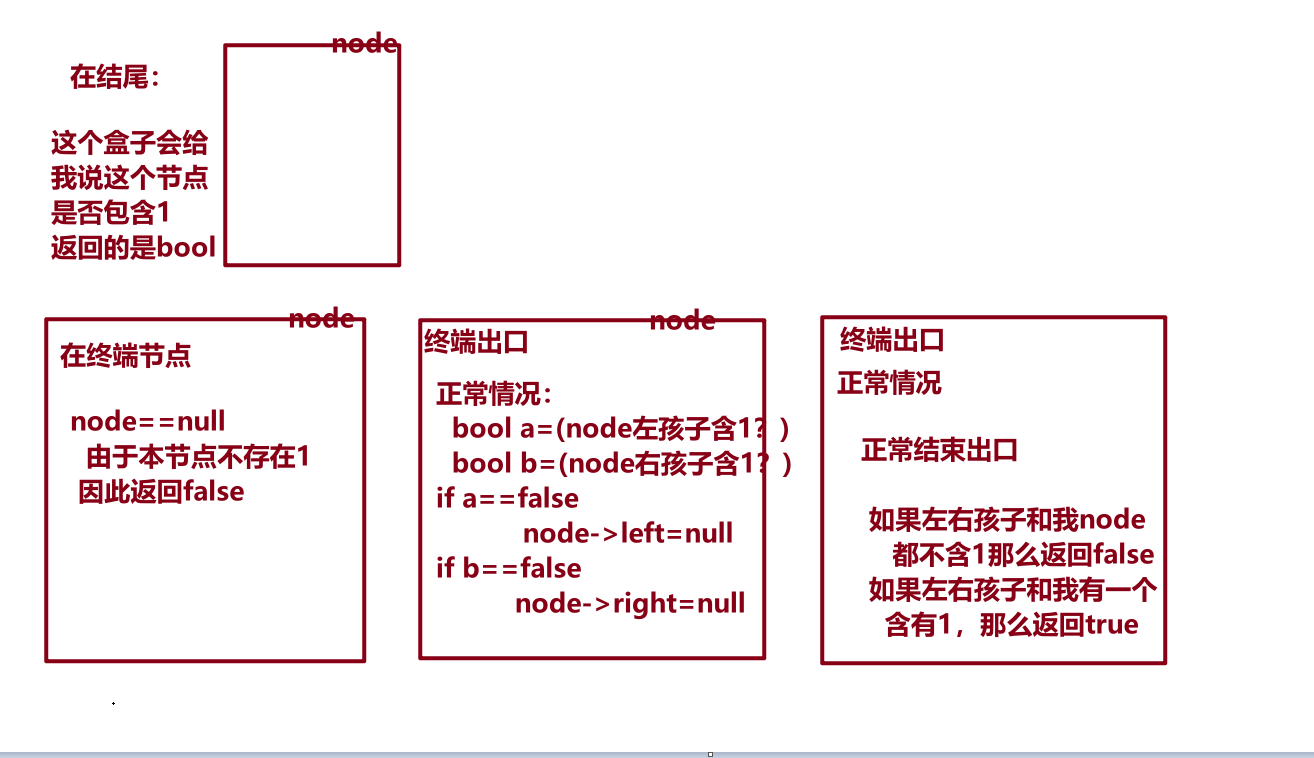
在这里插入图片描述
题目意思：减掉二叉树中所有节点的值为0的子树（如果0的子树中包含1，那么这个0不会被删除）
在这里插入图片描述

方法一：递归

在结尾：
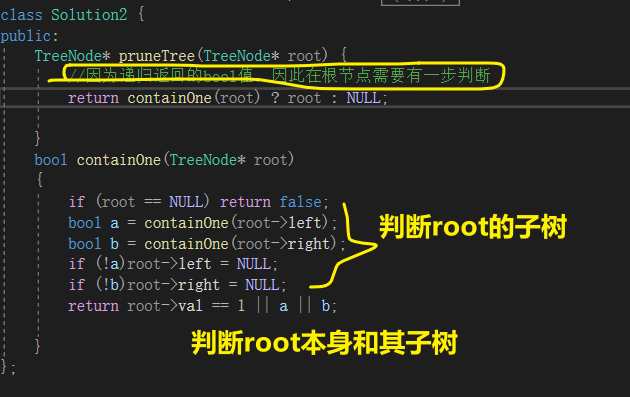
在这里插入图片描述

在这里插入图片描述

代码

class Solution2 {
public:
    TreeNode* pruneTree(TreeNode* root) {
        //因为递归返回的bool值，因此在根节点需要有一步判断
        return containOne(root) ? root : NULL;

    }
    bool containOne(TreeNode* root)
    {
        if (root == NULL) return false;
        bool a = containOne(root->left);
        bool b = containOne(root->right);
        if (!a)root->left = NULL;
        if (!b)root->right = NULL;
        return root->val == 1 || a || b;

    }
};

也可以用一个函数处理
在这里插入图片描述
在这里插入图片描述
上面这些都可以理解为后序遍历，最后处理的当前节点。

剑指 Offer II 048. 序列化与反序列化二叉树

序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。

请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

输入：root = [1,2,3,null,null,4,5]
输出：[1,2,3,null,null,4,5]

题目意思实现两个函数，一个将string字符串（不是数组）实现为树结构返回根节点，一个是将根节点返回为string字符串。

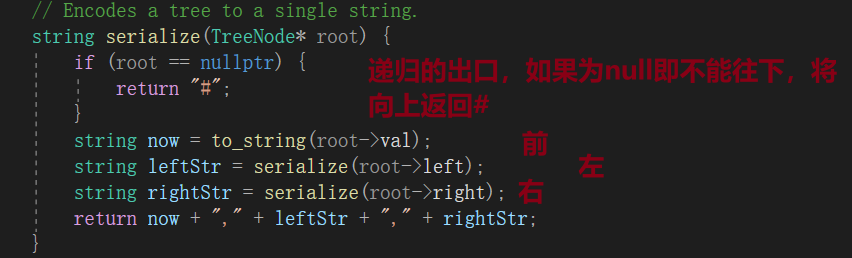
方法：前序遍历

仅使用前序遍历无法确定一棵二叉树，因为不知道下一个是往下还是结束，那么加上空节点表示当前分支已经结束了，让它继续向下一个进行，因此要包含空节点才可以，因此序列化一个二叉树要将空也加入。
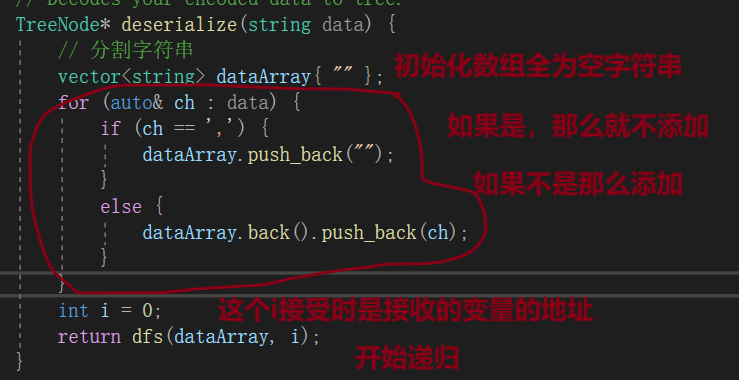
在这里插入图片描述
反序列化。
反序列化先将字符串按照逗号分成各个节点，然后前序递归
在这里插入图片描述
开始前序遍历
在这里插入图片描述

代码

class Codec {
public:
    // Encodes a tree to a single string.
    string serialize(TreeNode* root) {
        if (root == nullptr) {
            return "#";
        }
        string now = to_string(root->val);
        string leftStr = serialize(root->left);
        string rightStr = serialize(root->right);
        return now + "," + leftStr + "," + rightStr;
    }

    // Decodes your encoded data to tree.
    TreeNode* deserialize(string data) {
        // 分割字符串
        vector<string> dataArray{ "" };
        for (auto& ch : data) {
            if (ch == ',') {
                dataArray.push_back("");
            }
            else {
                dataArray.back().push_back(ch);
            }
        }
        int i = 0;
        return dfs(dataArray, i);
    }

private:
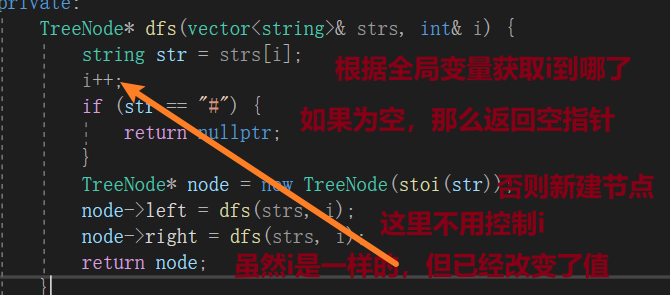
    TreeNode* dfs(vector<string>& strs, int& i) {
        string str = strs[i];
        i++;
        if (str == "#") {
            return nullptr;
        }
        TreeNode* node = new TreeNode(stoi(str));
        node->left = dfs(strs, i);
        node->right = dfs(strs, i);
        return node;
    }
    template <class T>
    void printVector(vector<T>ve) {
        cout << "vector的内容为" << " ";
        for (auto& ch : ve) {
            cout << ch << "  ";
        }
        cout << endl;

    }
};

剑指 Offer II 049. 从根节点到叶节点的路径数字之和

给定一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。

每条从根节点到叶节点的路径都代表一个数字：

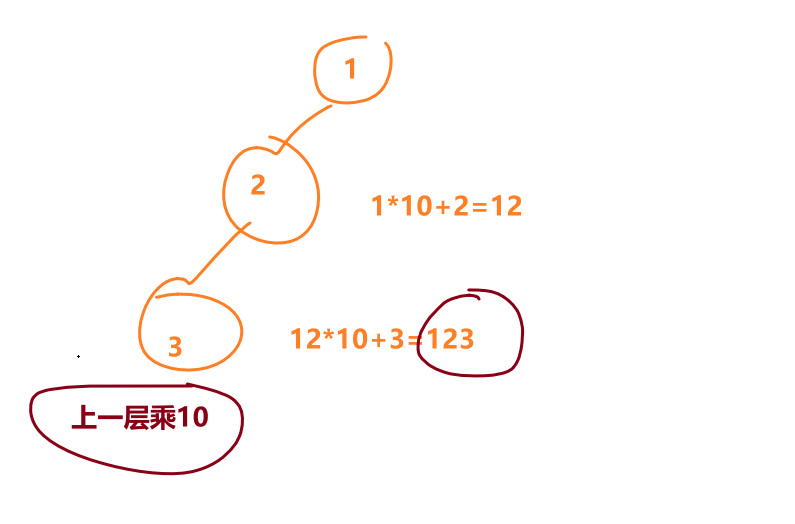
例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的 所有数字之和 。

输入：root = [1,2,3]
输出：25
解释：
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此，数字总和 = 12 + 13 = 25

题目意思是将所有从根到叶子节点的路径的值加起来。

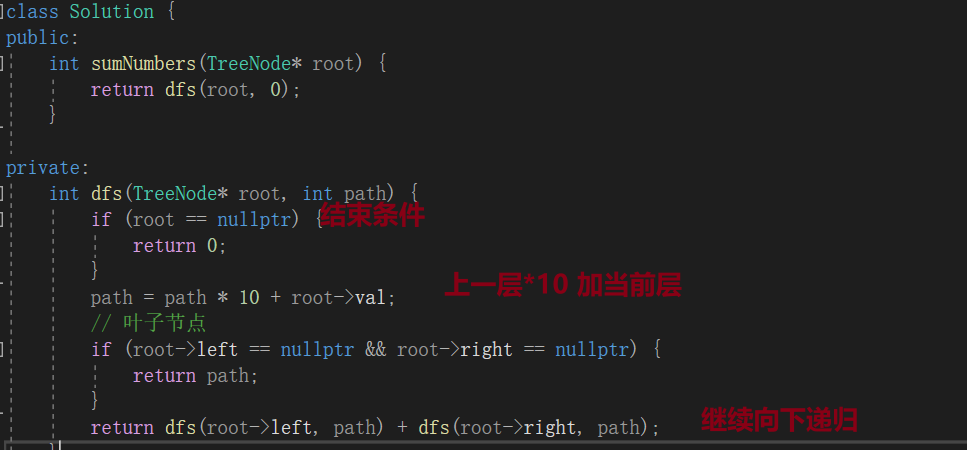
在这里插入图片描述

方法： 前序遍历（深度遍历）

在这里插入图片描述

代码

class Solution {
public:
    int sumNumbers(TreeNode* root) {
        return dfs(root, 0);
    }

private:
    int dfs(TreeNode* root, int path) {
        if (root == nullptr) {
            return 0;
        }
        path = path * 10 + root->val;
        // 叶子节点
        if (root->left == nullptr && root->right == nullptr) {
            return path;
        }
        return dfs(root->left, path) + dfs(root->right, path);
    }
};

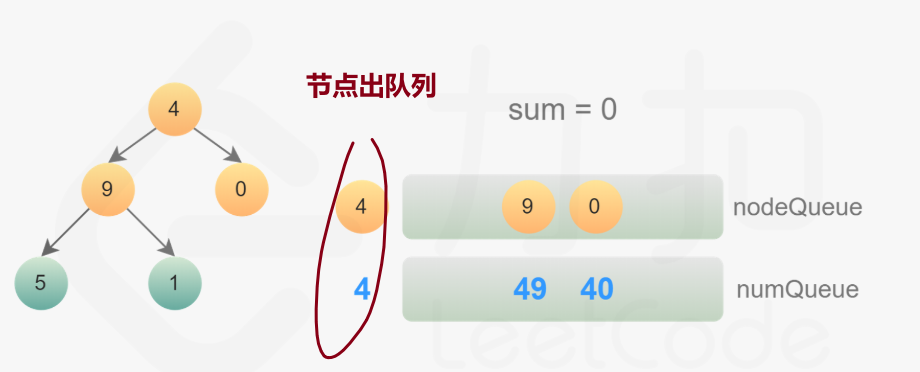
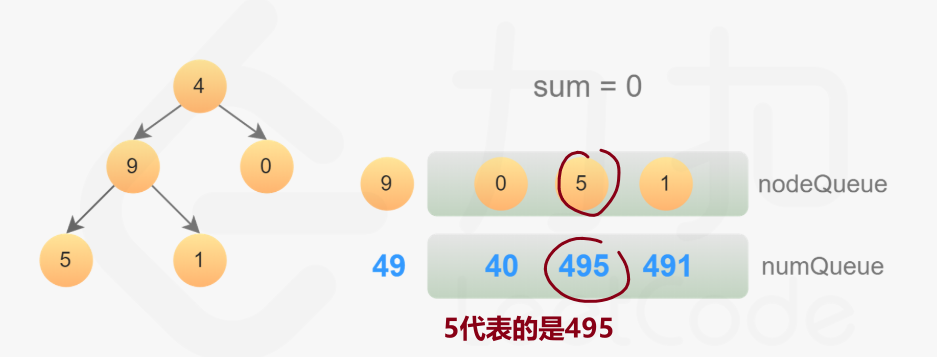
方法二：层序遍历（广度优先）

维护两个队列，第一个队列存放节点，一个存放到该节点的拥有的值，比如1->2，第一个队列存放1 2
第二个队列存放1，12
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

代码

class Solution {
public:
    int sumNumbers(TreeNode* root) {
        if (root == nullptr) {
            return 0;
        }
        int sum = 0;
        queue<TreeNode*> nodeQueue;
        queue<int> numQueue;
        nodeQueue.push(root);
        numQueue.push(root->val);
        while (!nodeQueue.empty()) {
            TreeNode* node = nodeQueue.front();
            int num = numQueue.front();
            nodeQueue.pop();
            numQueue.pop();
            TreeNode* left = node->left;
            TreeNode* right = node->right;
            if (left == nullptr && right == nullptr) {
                sum += num;
            } else {
                if (left != nullptr) {
                    nodeQueue.push(left);
                    numQueue.push(num * 10 + left->val);
                }
                if (right != nullptr) {
                    nodeQueue.push(right);
                    numQueue.push(num * 10 + right->val);
                }
            }
        }
        return sum;
    }
};

剑指 Offer II 050. 向下的路径节点之和

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3

题目意思：给一个二叉树，找所有的从上到下的路径，要求和为目标值，返回路径的条数

方法一：暴力穷举所有路径

使用深度遍历即前序遍历去枚举所有路径
在这里插入图片描述

代码

class Solution {
public:
    int rootSum(TreeNode* root, int targetSum) {
        if (!root) {
            return 0;
        }

        int ret = 0;
        if (root->val == targetSum) {
            ret++;
        } 

        ret += rootSum(root->left, targetSum - root->val);
        ret += rootSum(root->right, targetSum - root->val);
        return ret;
    }

    int pathSum(TreeNode* root, int targetSum) {
        if (!root) {
            return 0;
        }
        
        int ret = rootSum(root, targetSum);
        ret += pathSum(root->left, targetSum);
        ret += pathSum(root->right, targetSum);
        return ret;
    }
};

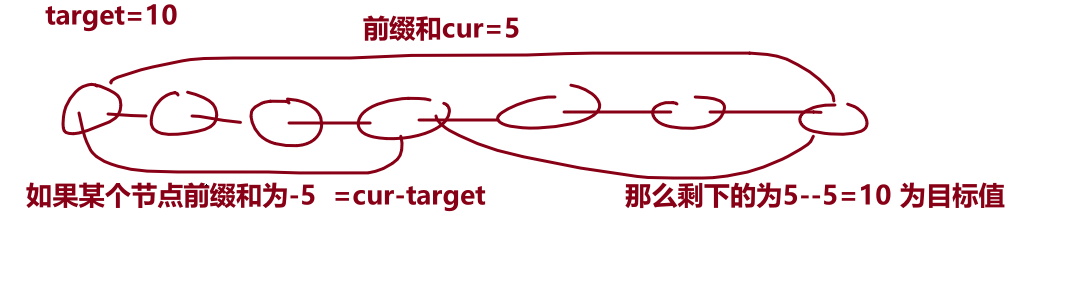
二叉树前缀和

简化问题为一维数据。

在这里插入图片描述

代码

class Solution {
public:
    unordered_map<long long, int> prefix;

    int dfs(TreeNode *root, long long curr, int targetSum) {
        if (!root) {
            return 0;
        }

        int ret = 0;
        curr += root->val;
        if (prefix.count(curr - targetSum)) {
            ret = prefix[curr - targetSum];
        }

        prefix[curr]++;
        ret += dfs(root->left, curr, targetSum);
        ret += dfs(root->right, curr, targetSum);
        prefix[curr]--;

        return ret;
    }

    int pathSum(TreeNode* root, int targetSum) {
        prefix[0] = 1;
        return dfs(root, 0, targetSum);
    }
};

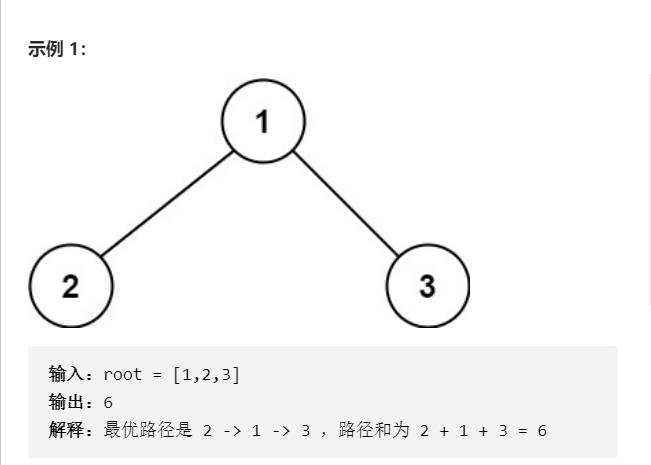
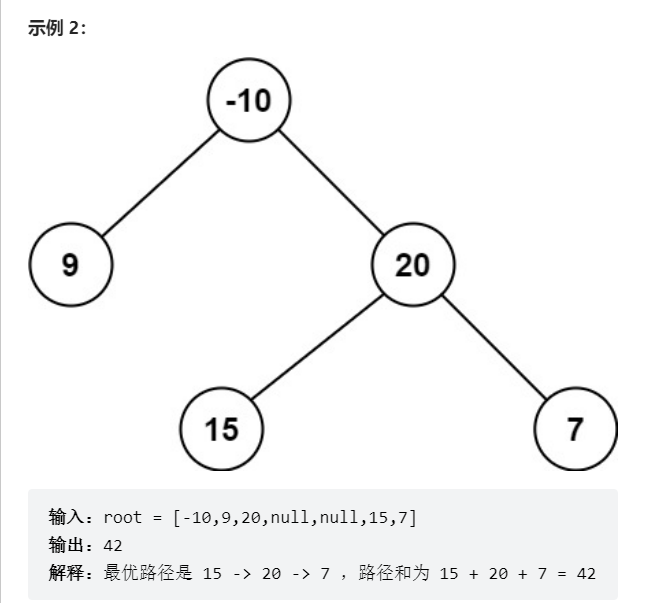
剑指 Offer II 051. 节点之和最大的路径

路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给定一个二叉树的根节点 root ，返回其 最大路径和，即所有路径上节点值之和的最大值。
在这里插入图片描述
在这里插入图片描述

题目要求最大的路径和，这里并不是图的路径问题，子树中一定有个根节点

方法：递归

在这里插入图片描述
在这里插入图片描述

代码

class Solution {
private:
    int maxSum = INT_MIN;

public:
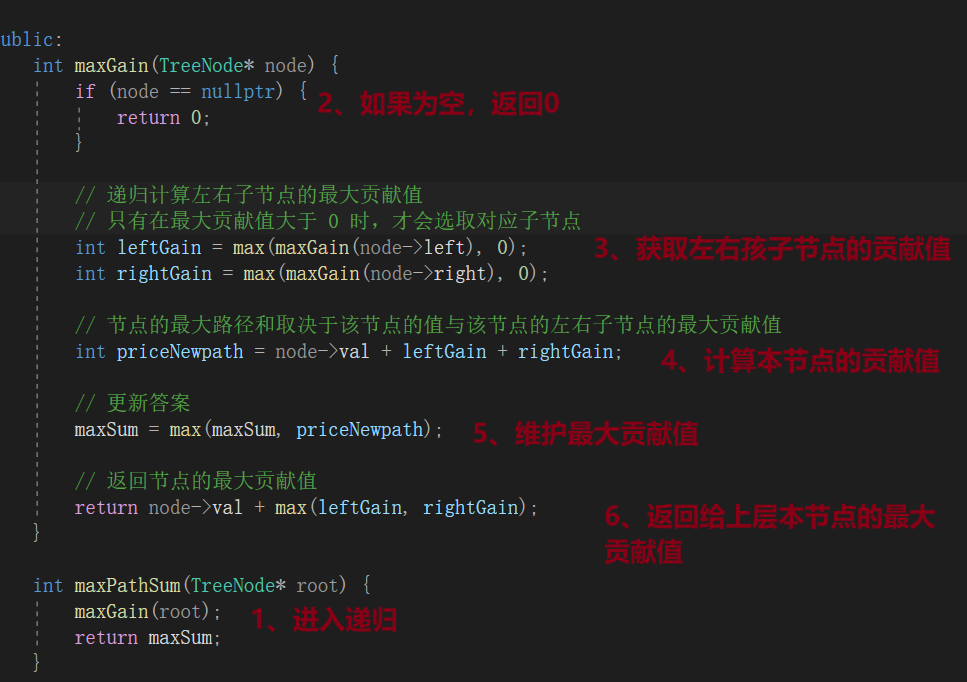
    int maxGain(TreeNode* node) {
        if (node == nullptr) {
            return 0;
        }

        // 递归计算左右子节点的最大贡献值
        // 只有在最大贡献值大于 0 时，才会选取对应子节点
        int leftGain = max(maxGain(node->left), 0);
        int rightGain = max(maxGain(node->right), 0);

        // 节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值
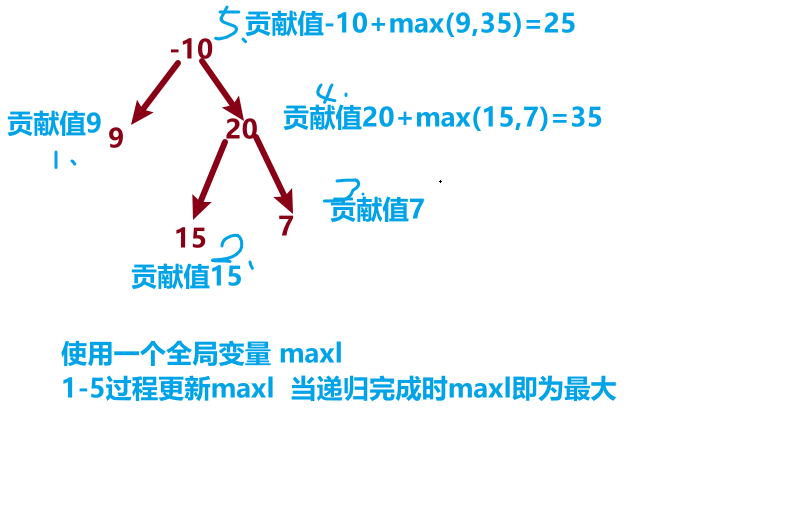
        int priceNewpath = node->val + leftGain + rightGain;

        // 更新答案
        maxSum = max(maxSum, priceNewpath);

        // 返回节点的最大贡献值
        return node->val + max(leftGain, rightGain);
    }

    int maxPathSum(TreeNode* root) {
        maxGain(root);
        return maxSum;
    }
};

剑指 Offer II 052. 展平二叉搜索树

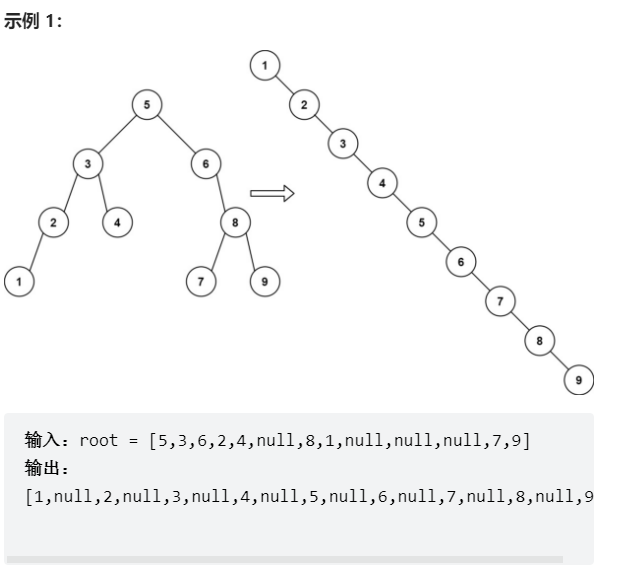
给你一棵二叉搜索树，请 按中序遍历 将其重新排列为一棵递增顺序搜索树，使树中最左边的节点成为树的根节点，并且每个节点没有左子节点，只有一个右子节点。

在这里插入图片描述
中序遍历展平

方法一：中序遍历存到数组中，根据数组重建二叉树

中序遍历得到的数组，数组里里面的次序就是二叉树的次序
在这里插入图片描述

代码

class Solution {
public:
    void inorder(TreeNode *node, vector<int> &res) {
        if (node == nullptr) {
            return;
        }
        inorder(node->left, res);
        res.push_back(node->val);
        inorder(node->right, res);
    }

    TreeNode *increasingBST(TreeNode *root) {
        vector<int> res;
        inorder(root, res);

        TreeNode *dummyNode = new TreeNode(-1);
        TreeNode *currNode = dummyNode;
        for (int value : res) {
            currNode->right = new TreeNode(value);
            currNode = currNode->right;
        }
        return dummyNode->right;
    }
};

方法二：使用一个全局变量存储临时根节点，在中序遍历中改变指针指向

在这里插入图片描述

代码

class Solution {
private:
    TreeNode *resNode;

public:
    void inorder(TreeNode *node) {
        if (node == nullptr) {
            return;
        }
        inorder(node->left);

        // 在中序遍历的过程中修改节点指向
        resNode->right = node;
        node->left = nullptr;
        resNode = node;

        inorder(node->right);
    }

    TreeNode *increasingBST(TreeNode *root) {
        TreeNode *dummyNode = new TreeNode(-1);
        resNode = dummyNode;
        inorder(root);
        return dummyNode->right;
    }
};

剑指 Offer II 053. 二叉搜索树中的中序后继

给定一棵二叉搜索树和其中的一个节点 p ，找到该节点在树中的中序后继。如果节点没有中序后继，请返回 null 。

节点 p 的后继是值比 p.val 大的节点中键值最小的节点，即按中序遍历的顺序节点 p 的下一个节点。

输入：root = [2,1,3], p = 1
输出：2
解释：这里 1 的中序后继是 2。请注意 p 和返回值都应是 TreeNode 类型。
题目意思，给个树，给个树上的节点，找到中序遍历的当前节点的下一个节点。

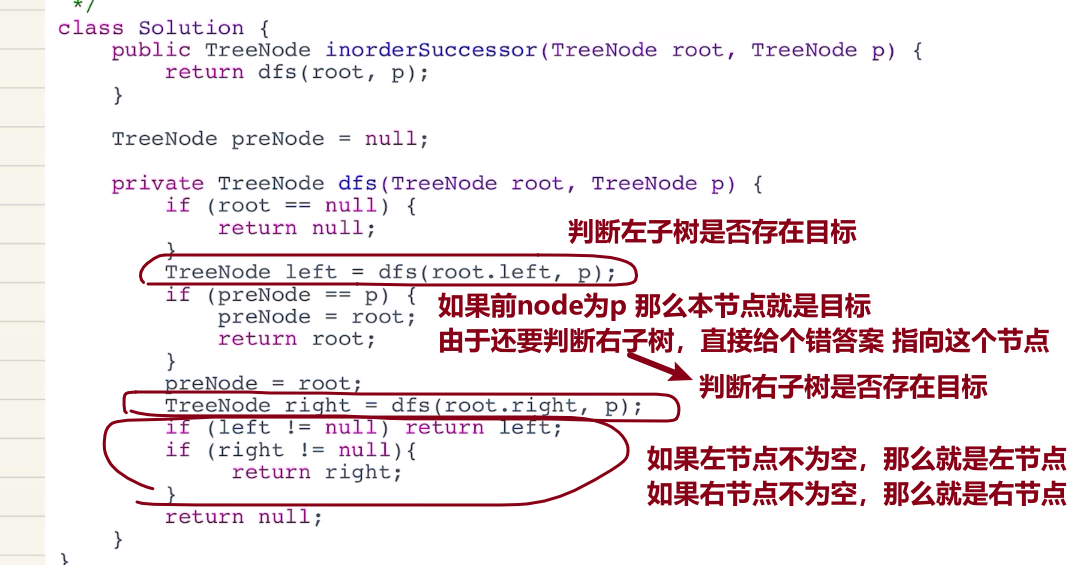
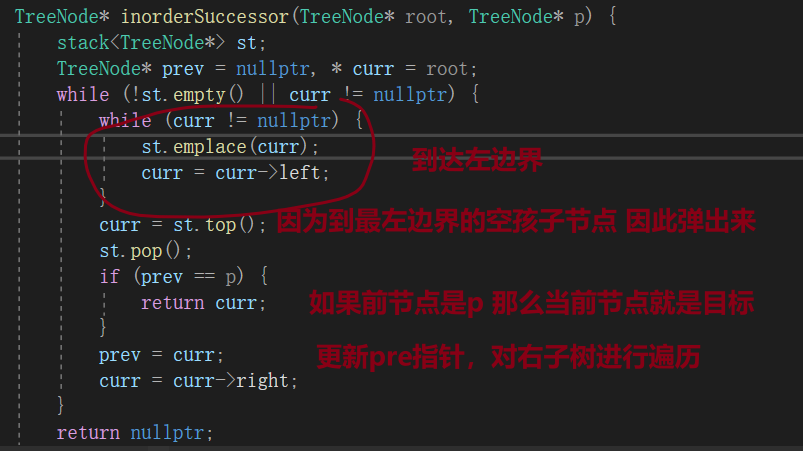
方法一：递归维护前一个节点，如果前一个节点是p，那么当前节点就是目标

维护前节点，使用递归进行中序遍历，在中序遍历的左遍历时，如果前节点是p，那么就让left=当前节点，因为已经找到了，还要进行右子树遍历，那么还是要更新下前电点的值，不让右遍历再次找到。
最后如果左节点不为空，那就是目标，如果右节点不为空，那就是目标。

在这里插入图片描述

方法二：用栈模拟递归

思路还是维护pre指针，如果pre是p，那么当前节点就是目标
在这里插入图片描述

剑指 Offer II 054. 所有大于等于节点的值之和

给定一个二叉搜索树，请将它的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和。
提醒一下，二叉搜索树满足下列约束条件：
节点的左子树仅包含键 小于 节点键的节点。
节点的右子树仅包含键 大于 节点键的节点。
左右子树也必须是二叉搜索树。
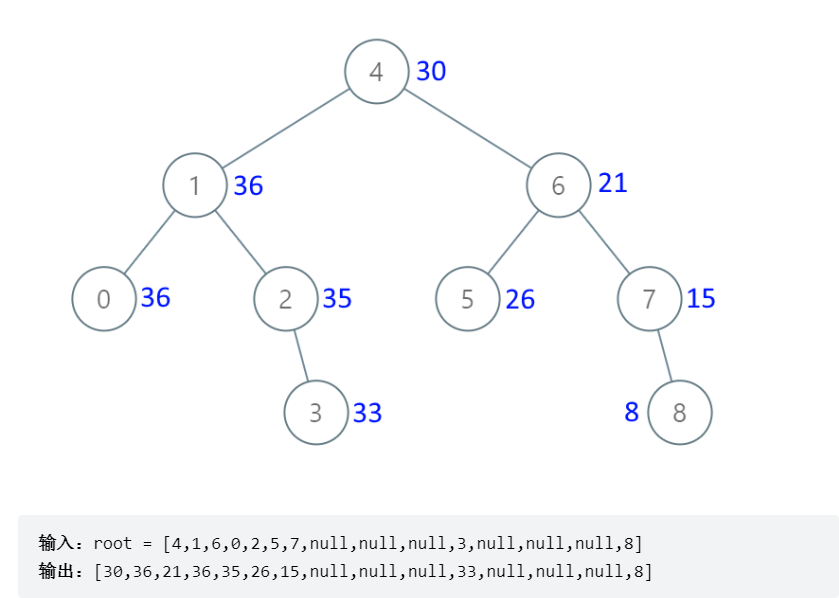
在这里插入图片描述
题目描述：给的是二叉搜索树，某个节点的左子树都小于这个节点，节点的右子树都大于这个节点。
然后题目想把该节点的左子树包含自己全加起来替换当前节点的值

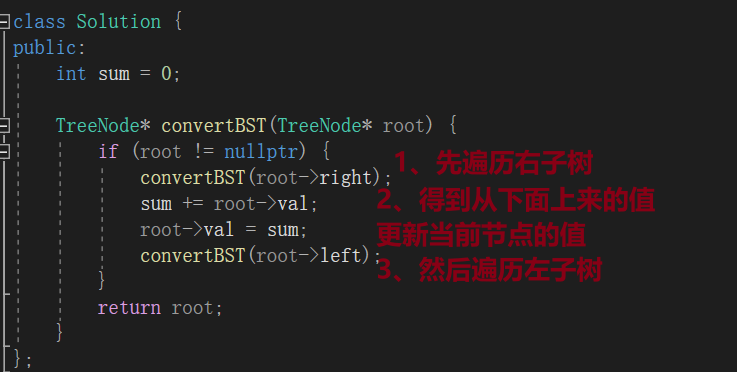
方法一：反向中序遍历：右中左

右遍历得到的就是从下面加上来的数，再中进行处理
在这里插入图片描述

代码

class Solution {
public:
    int sum = 0;

    TreeNode* convertBST(TreeNode* root) {
        if (root != nullptr) {
            convertBST(root->right);
            sum += root->val;
            root->val = sum;
            convertBST(root->left);
        }
        return root;
    }
};

方法二：Morris 遍历

剑指 Offer II 055. 二叉搜索树迭代器

实现一个二叉搜索树迭代器类BSTIterator ，表示一个按中序遍历二叉搜索树（BST）的迭代器：

BSTIterator(TreeNode root) 初始化 BSTIterator 类的一个对象。BST 的根节点 root 会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字，且该数字小于 BST 中的任何元素。
boolean hasNext() 如果向指针右侧遍历存在数字，则返回 true ；否则返回 false 。
int next()将指针向右移动，然后返回指针处的数字。
注意，指针初始化为一个不存在于 BST 中的数字，所以对 next() 的首次调用将返回 BST 中的最小元素。

可以假设 next() 调用总是有效的，也就是说，当调用 next() 时，BST 的中序遍历中至少存在一个下一个数字。
题目描述：中序遍历二叉树，BSTIterator初始化类的对象（没有用）next()返回中序遍历的下一个节点的值，hashnext()判断是否还有下一个节点

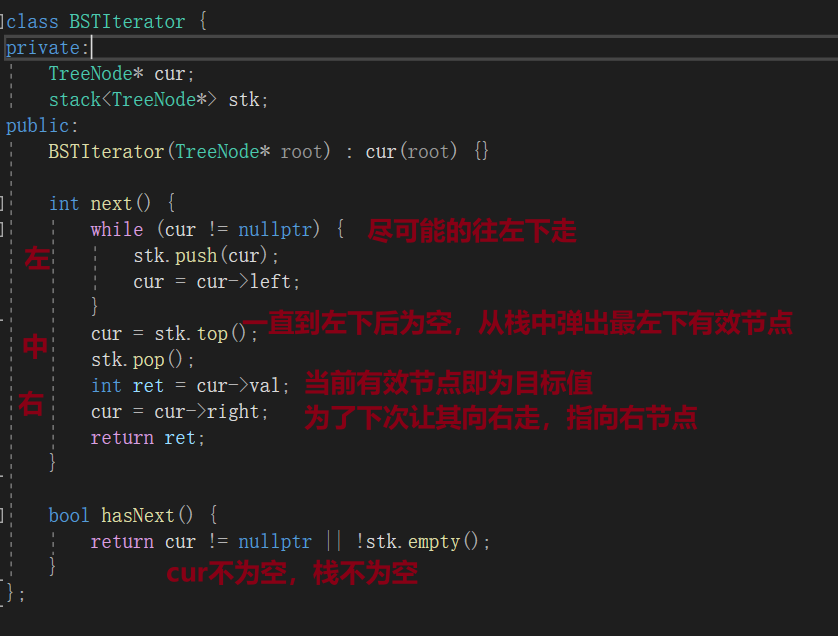
方法一：迭代

next没必要获得所有元素，如果树很大就会占内存
用一个cur表示当前节点的运行位置，用一个栈来进行迭代。但是左中右，在完成"中"进入右节点后（即上次next函数执行完成后），右节点要一直往左下方走，所以下面上来就一直往下走，然后就是中，中就是目标，然后将指针指向右节点。
在这里插入图片描述

方法二：中序遍历将得来的值保存到数组中

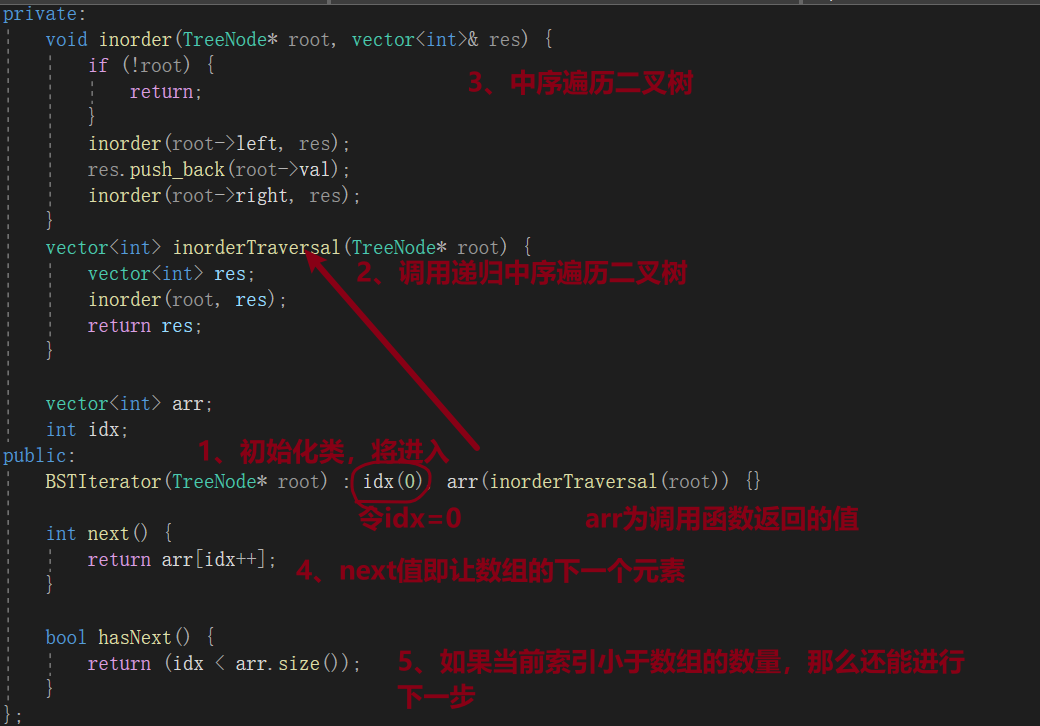
在这里插入图片描述

代码

class BSTIterator {
private:
    void inorder(TreeNode* root, vector<int>& res) {
        if (!root) {
            return;
        }
        inorder(root->left, res);
        res.push_back(root->val);
        inorder(root->right, res);
    }
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        inorder(root, res);
        return res;
    }
    
    vector<int> arr;
    int idx;
public:
    BSTIterator(TreeNode* root): idx(0), arr(inorderTraversal(root)) {}
    
    int next() {
        return arr[idx++];
    }
    
    bool hasNext() {
        return (idx < arr.size());
    }
};

剑指 Offer II 056. 二叉搜索树中两个节点之和

给定一个二叉搜索树的 根节点 root 和一个整数 k , 请判断该二叉搜索树中是否存在两个节点它们的值之和等于 k 。假设二叉搜索树中节点的值均唯一。

输入: root = [8,6,10,5,7,9,11], k = 12
输出: true
解释: 节点 5 和节点 7 之和等于 12

方法一：遍历二叉树，将值存储到哈希表中

遍历到某个节点时，判断哈希表中是否存在目标值-当前值
在这里插入图片描述

方法二：广度(层次)遍历插入到哈希表

方法三：遍历二叉树，将节点值保存到数组中，再用双指针

由于搜索树中序遍历带有次序

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
《统计学习方法》第4章朴素贝叶斯法与贝叶斯估计
基于ssm+vue基于elementui的工厂物料管理系统设计与实现【开题+程序+论文】
操作系统复习1
二叉树遍历的应用
Java出现OutOf MemoryError（OOM 错误)的原因有哪些？出现OOM错误后，怎么解决？
大学生恋爱情况分析
prim(模板）
(java毕设源码下载)基于java(springboot)问卷调查管理系统
GitHub上README写法暨GFM语法解读
JavaMail邮件发送相关案例
;