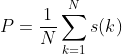1 连续高斯白噪声和离散高斯白噪声有什么异同?
实际场景中的高斯白噪声都是时间上连续的,而离散的噪声则常应用于计算机仿真中。离散噪声就是从连续的噪声数据中采样得到。
2 两者的功率谱有什么含义?
连续高斯白噪声的功率谱为功率密度(w/Hz或J)随频率分量(Hz)变化的情况,平均功率即为曲线的积分;已知白噪声的功率谱为常数,每个时间点的能量为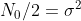
另外,对于窄带高斯白噪声,假设单边带宽为B,则平均功率有限,为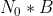
功率谱的定义如下:
平均功率的计算如下:
离散高斯白噪声的功率谱为功率(w)随点数的变化,所有功率点之和为能量(由于离散时间,因此每个点的功率存在,注意,这里的总和不再是平均功率!),这里的平均功率则为能量除以点数,为有限值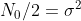
另外,对于有限点数情况,能量有限,平均功率不变。
功率谱的定义如下:
平均功率的计算如下:
下附离散高斯白噪声代码验证
%% 结论:离散高斯白噪声功率谱意义:每个点对应的为功率(w),而非功率密度(w/Hz)
% 因此功率谱为常数,则无数个点的总功率为无限大,即能量无限大,而平均功率则为常数sigma^2
% 对高斯噪声随机采样点进行排序,则功谱不再为常数,但总功率不变
% 高斯噪声的功率计算方法有三种:
% 由高斯分布的方差(0.8^2)直接得出;由功率谱的幅度平均得出;由时域或频域能量除以点数N得出
N=100;fftN=100;
x1=0.8*randn(1,N);%功率计算方法1
x2=fft(x1,fftN);
x3=abs(x2).^2/N;%功率谱
x4=sum(x3)/N;%平均功率,功率计算方法2
plot(x3);
y1=sort(x1);
y2=fft(y1,fftN);
y3=abs(y2).^2/N;%功率谱
y4=sum(y3)/N;
figure(2);
plot(y3);
%时域能量=频域能量
e1=sum(x1.*x1);f1=sum(abs(x2).^2)/N;
e2=sum(y1.*y1);f2=sum(abs(y2).^2)/N;
%时域功率=频域功率
p1=e1/N;fp1=f1/N;%功率计算方法3
p2=e2/N;fp2=f2/N;
0.8*0.8%理论功率
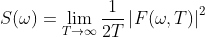
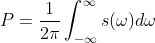
![S(k)=\frac{1}{N}\left | X[k]\right |^{2}](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvMDdmZTcyNGM2YzAyMDBjM2I2NjEyNTU5NWE0NzkxMzYuZ2lm)