C#，图论与图算法，输出无向图“欧拉路径”的弗勒里（Fleury Algorithm）算法和源程序

1 欧拉路径

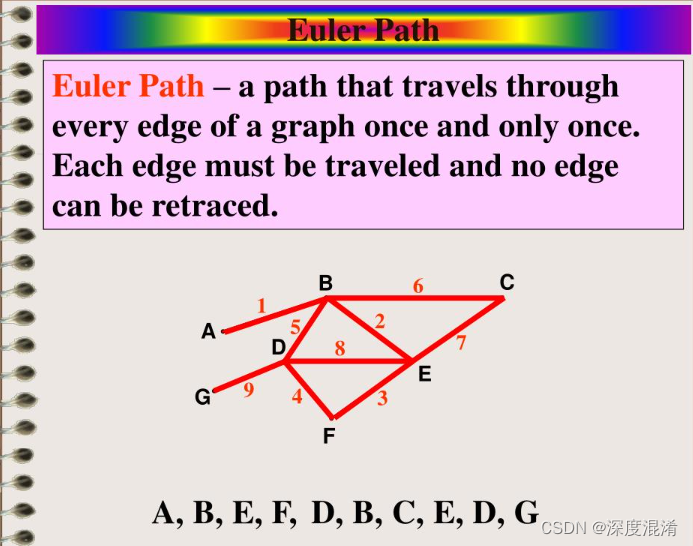
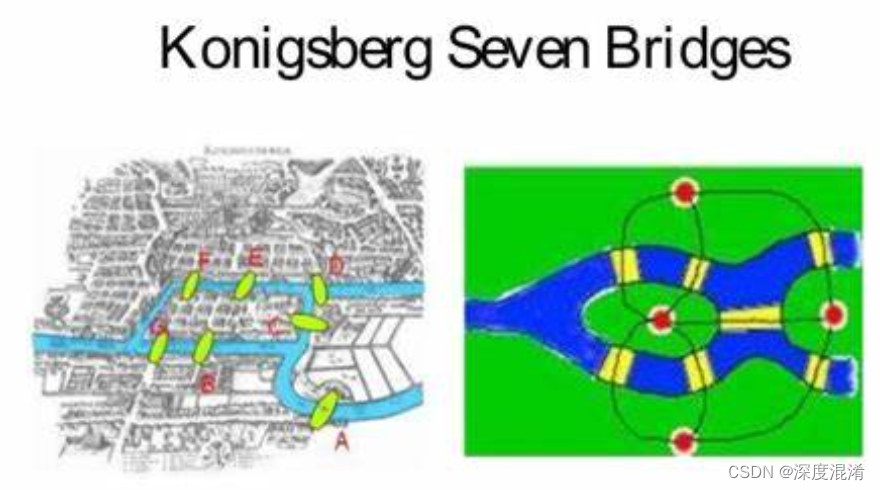
欧拉路径是图中每一条边只访问一次的路径。欧拉回路是在同一顶点上开始和结束的欧拉路径。

这里展示一种输出欧拉路径或回路的算法。

以下是Fleury用于打印欧拉轨迹或循环的算法（源）。

1、确保图形有0个或2个奇数顶点。
2、如果有0个奇数顶点，则从任意位置开始。如果有两个奇数顶点，请从其中一个开始。
3、沿边一次一条。如果要在桥和非桥之间进行选择，请始终选择非桥。
4、边缘用完时停止。

这个想法是，“不要过桥”，这样我们就可以回到一个顶点并遍历其余的边。

2 算法

在下面的代码中，假设给定的图具有欧拉轨迹或回路。主要焦点是打印欧拉轨迹或回路。我们可以使用isEulerian（）首先检查给定图中是否存在欧拉轨迹或回路。

我们首先找到必须是奇点的起点（如果有奇点），并将其存储在变量“u”中。如果奇数顶点为零，则从顶点“0”开始。我们调用printEulerUtil（）来打印从u开始的Euler tour。我们遍历u的所有相邻顶点，如果只有一个相邻顶点，我们会立即考虑它。如果有多个相邻顶点，则仅当边u-v不是桥时，才考虑相邻v。如何确定给定的边是否是桥？我们计算从u可到达的几个顶点。我们移除边u-v，然后再次计算从u可到达的顶点的数量。如果可到达顶点的数量减少，则边u-v是一个桥。为了计算可到达的顶点，我们可以使用BFS或DFS，我们在上面的代码中使用了DFS。函数DFSCount（u）返回可从u访问的多个顶点。

处理完边（包括在Euler教程中）后，我们将其从图形中移除。要删除边，我们将邻接列表中的顶点条目替换为-1。请注意，简单地删除节点可能不起作用，因为代码是递归的，并且父调用可能位于邻接列表的中间。

参考：

C#，图（Graph）的数据结构设计与源代码https://blog.csdn.net/beijinghorn/article/details/125133711?spm=1001.2014.3001.5501

3 源代码：

using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;

namespace Legalsoft.Truffer.Algorithm
{
	public partial class Graph
	{
		private void RemoveEdge(int u, int v)
		{
			Adjacency[u].Remove(v);
			Adjacency[v].Remove(u);
		}

		private void Euler_Tour()
		{
			int u = 0;
			for (int i = 0; i < Node_Number; i++)
			{
				if (Adjacency[i].Count % 2 == 1)
				{
					u = i;
					break;
				}
			}

			Euler_Tour_Utility(u);
		}

		public List<string> Tours = new List<string>();

		private void Euler_Tour_Utility(int u)
		{
			for (int i = 0; i < Adjacency[u].Count; i++)
			{
				int v = Adjacency[u][i];

				if (Is_Valid_Next_Edge(u, v))
				{
					Tours.Add(u + " - " + v + " ");

					RemoveEdge(u, v);
					Euler_Tour_Utility(v);
				}
			}
		}

		private bool Is_Valid_Next_Edge(int u, int v)
		{
			if (Adjacency[u].Count == 1)
			{
				return true;
			}

			bool[] isVisited = new bool[this.Node_Number];
			int count1 = DFS_Count_Reach(u, isVisited);

			RemoveEdge(u, v);
			isVisited = new bool[this.Node_Number];
			int count2 = DFS_Count_Reach(u, isVisited);

			AddEdge(u, v);
			return (count1 > count2) ? false : true;
		}

		private int DFS_Count_Reach(int v, bool[] isVisited)
		{
			isVisited[v] = true;

			int count = 1;
			foreach (int i in Adjacency[v])
			{
				if (!isVisited[i])
				{
					count = count + DFS_Count_Reach(i, isVisited);
				}
			}
			return count;
		}
	}

	public static partial class GraphDrives
	{
		public static string Euler_Tours()
		{
			StringBuilder sb = new StringBuilder();
			Graph g1 = new Graph(4);
			g1.AddEdge(0, 1);
			g1.AddEdge(0, 2);
			g1.AddEdge(1, 2);
			g1.AddEdge(2, 3);
			sb.AppendLine("Graph 1 Euler_Tours:<br>");
			sb.AppendLine(String.Join("<br>", g1.Tours.ToArray()) + "<br>");

			Graph g2 = new Graph(3);
			g2.AddEdge(0, 1);
			g2.AddEdge(1, 2);
			g2.AddEdge(2, 0);
			sb.AppendLine("Graph 2 Euler_Tours:<br>");
			sb.AppendLine(String.Join("<br>", g2.Tours.ToArray()) + "<br>");

			Graph g3 = new Graph(5);
			g3.AddEdge(1, 0);
			g3.AddEdge(0, 2);
			g3.AddEdge(2, 1);
			g3.AddEdge(0, 3);
			g3.AddEdge(3, 4);
			g3.AddEdge(3, 2);
			g3.AddEdge(3, 1);
			g3.AddEdge(2, 4);
			sb.AppendLine("Graph 3 Euler_Tours:<br>");
			sb.AppendLine(String.Join("<br>", g3.Tours.ToArray()) + "<br>");

			return sb.ToString();
		}
	}
}