一、弗洛伊德·沃肖尔算法
Floyd-Warshall算法是图的最短路径算法。与Bellman-Ford算法或Dijkstra算法一样,它计算图中的最短路径。然而,Bellman Ford和Dijkstra都是单源最短路径算法。这意味着他们只计算来自单个源的最短路径。另一方面,Floyd Warshall计算输入图中每对顶点之间的最短距离。
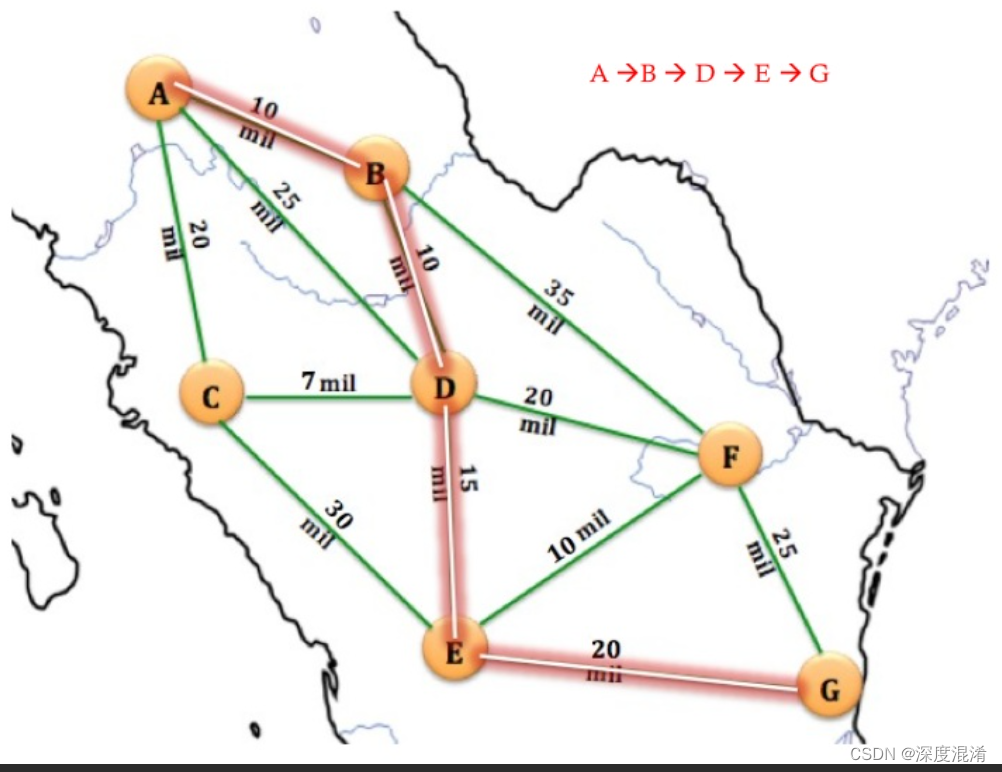
假设你有5个朋友:比利、珍娜、卡西、艾丽莎和哈里。你知道有几条路连接他们的一些房子,你知道这些路的长度。但是,弗洛伊德·沃沙尔可以利用你所知道的,并根据这些信息为你提供最佳路线。例如,看看下面的图表,它显示了从一个朋友到另一个朋友的路径以及相应的距离。
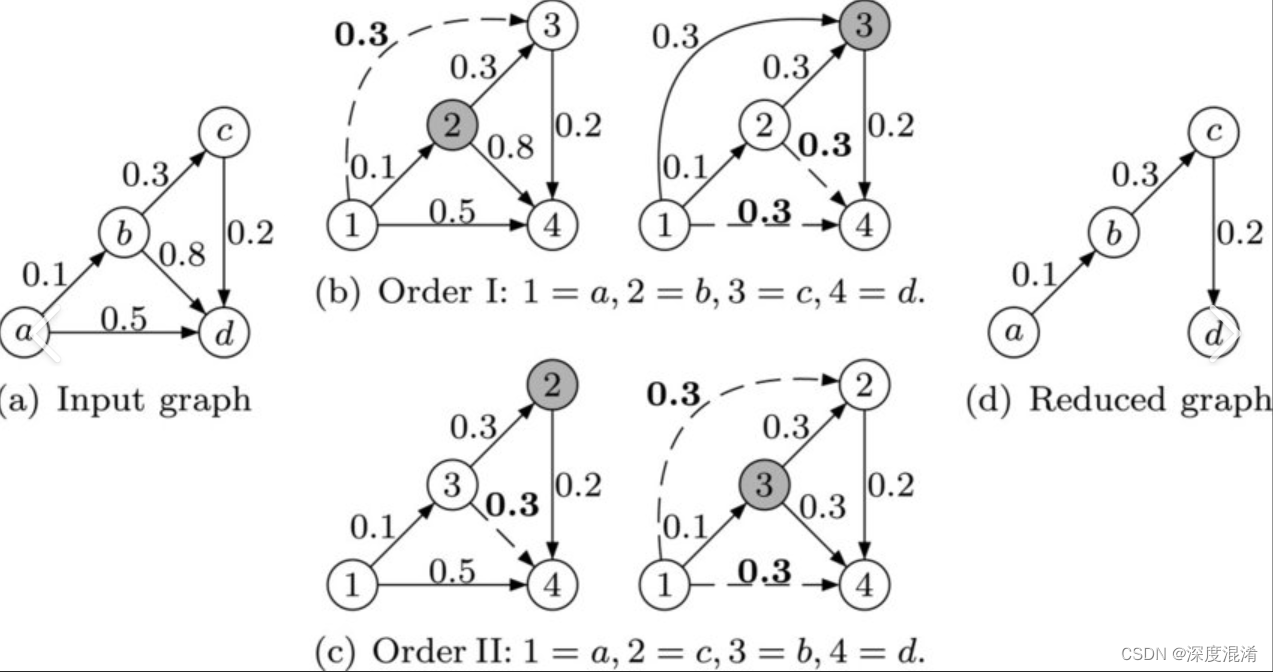
我们初始化解矩阵的第一步与输入图矩阵相同。然后,我们通过将所有顶点视为中间顶点来更新解矩阵。其思想是一个接一个地拾取所有顶点,并更新所有最短路径,其中包括拾取的顶点作为最短路径中的中间顶点。当我们选取顶点数 k 作为中间顶点时,我们已经考虑了顶点{0,1,2,..k-1}作为中间顶点。对于源顶点和目标顶点的每一对(I,j),都有两种可能的情况。 1) k 在从 I 到 j 的最短路径中不是中间顶点,我们保持 dist[i][j]的值不变。 2) k 是从 I 到 j 的最短路径中的中间顶点,我们将 dist[i][j]的值更新为 dist[I][k]+dist[k][j]if dist[I][j]>dist[I][k]+dist[k][j] 下图显示了以上全对最短路径问题中的最优子结构性质。
二、Floyd-Warshall算法的应用
1、最短距离
弗洛伊德·沃沙尔将告诉每对朋友之间的最佳距离。它将清楚地告诉您,从Alyssa的房子到Harry的房子的最快路径是连接边,其权重为1。但是,它也会告诉你,从比利家到珍娜家的最快方式是先经过卡西家,然后是艾丽莎家,然后是哈利家,最后才到珍娜家。这就是弗洛伊德·华肖的力量;无论你现在在哪所房子,它都会告诉你去其他房子的最快方式。
Floyd-Warshall算法是动态规划的一个例子。它将问题分解为较小的子问题,然后将这些子问题的答案结合起来,以解决较大的初始问题。想法是这样的:要么从A到C的最快路径是从A到C的最快路径,要么是从A到B的最快路径加上从B到C的最快路径。
Floyd Warshall在网络方面非常有用,类似于最短路径问题的解决方案。但是,它在管理路线上的多个站点时更有效,因为它可以计算所有相关节点之间的最短路径。事实上,Floyd Warshall的一次运行可以为您提供有关静态网络的所有信息,以优化大多数类型的路径。它在计算矩阵求逆时也很有用。
2、求解离散数学中传递闭包
离散数学中传递闭包怎么求?传递闭包的求法就是:通过反复求矩阵的幂,直到结果不在变化为止!可以选择用warshall法,不断的运行,直到MR[n][i],MR[i][n]都为1时使得MR[i][j]为1,不然的话还是要继续不断的运行,直到结果MR[n][i],MR[i][n]都为1时使得MR[i][j]为1就停止。
在这个式子中,a数组中为布尔数组,主要是用来描述两个节点是不是出于一个相连的地位上,可以看出做这样一个无权图的邻接矩阵,在算法过程中是和Floyd相当相似,而且三重循环的话是需要列出中间的每一个节点,不过对于传递闭包而言的话,只是需要求出两个节点是不是相连,并不用在进一步的求解两个线路中间的最短路径了。
传递闭包最为简单的技术就是选择采用弗洛伊德算法,选择用Floyd-Warshall算法能够最简便的解决任意两点之间最简单的路径中的一个算法,而且还可以这个却的出力有向图或者负权。
时间复杂度: O(V^3) 上面的程序只打印最短的距离。我们还可以通过将前置信息存储在单独的 2D 矩阵中来修改解决方案以打印最短路径。 同样,INF 的值可以从 limits.h 取为 INT_MAX,以确保我们处理最大可能值。当我们取 INF 为 INT_MAX 时,需要改变上述程序中的 if 条件,以避免算术溢出。
三、算法思路
1、算法所要解决的问题称为多源最短路径问题,算法完成后可求出任意两点之间的最短路径,所以既然他这么简单,那么这五行码有什么意义?
A和 B的直接距离是6,那么我们该如何缩小它们之间的距离?
其算法的具体思想如下:一想,我只经过 C这个点的中转就可以让
2、相邻矩阵 dist存储路径,而最终状态表示点的最短路径。若没有直接关联的点,默认值为一个非常大的值(不要溢出)!并且自身的长度是0。
将从1到 n点依次添加到图中。每一点都加入以测试是否有路径长度被改变。
并以图中每个点(i, j两次循环)为例,判断每个点对距离是否因所加入的点而变化最小。若有变化,则两点(i、 j)距离将改变。
非常简单,我们只需通过其它点的中转就可以了,这里我们就是 C点,可以让 A和 B之间的距离到达5,然后我再想一想,我只经过 C这个点的中转就可以让他们的距离变小,
为了确定这个周期的最外层循环被用于传递这个周期中的哪个点。即,第一次循环是以一号顶点为中转站,观察是否可以将其他点间的距离减小,第二个循环是在第一个循环的基础。
总结: warshall算法的时间复杂度为 O (n3),实现简单,适用于处理稠密图与顶点关。
四、实现代码
参考:
源代码(POWER BY TRUFFER):
using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
public partial class Graph
{
public int[,] Floyd_Warshall()
{
int V = Node_Number;
int[,] dist = new int[V, V];
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
dist[i, j] = Matrix[i, j];
}
}
for (int k = 0; k < V; k++)
{
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
if (dist[i, k] + dist[k, j] < dist[i, j])
{
dist[i, j] = dist[i, k] + dist[k, j];
}
}
}
}
return dist;
}
}
public static partial class GraphDrives
{
public static string Floyd_Warshall()
{
StringBuilder sb = new StringBuilder();
int INF = 99999;
int[,] m = {
{ 0, 5, INF, 10 },
{INF, 0, 3, INF },
{INF, INF, 0, 1 },
{INF, INF, INF, 0 }
};
Graph g = new Graph(m);
g.AdjacencyMatrix();
int[,] dist = g.Floyd_Warshall();
return Algorithm_Gallery.ToHtml(dist);
}
}
}


 https://blog.csdn.net/beijinghorn/article/details/125133711?spm=1001.2014.3001.5501
https://blog.csdn.net/beijinghorn/article/details/125133711?spm=1001.2014.3001.5501