Leiden算法出自2019年的论文《From Louvain to Leiden: guaranteeing well-connected communities》,它是Louvain算法的改进社区发现算法,相比Louvain得到的社区质量更高,因为其移动策略速度也更快。Leiden算法也是以论文作者所在城市来命名的。
Louvain算法的缺陷
Louvain算法可能会造成生成的社区内部是未连通的,这种情况通常是社区的某一个部分是由经过社区外节点的路径与社区内的其他部分连接在一起的。回顾一下Louvain算法,它主要分为两个阶段:模块度优化和社区合并,这两个阶段不断进行迭代直到无法得到更优的结果。在模块度优化时在旧社区起桥接作用的节点可能会被加入到其他社区中使得原来的旧社区变成了内部不连通的社区。
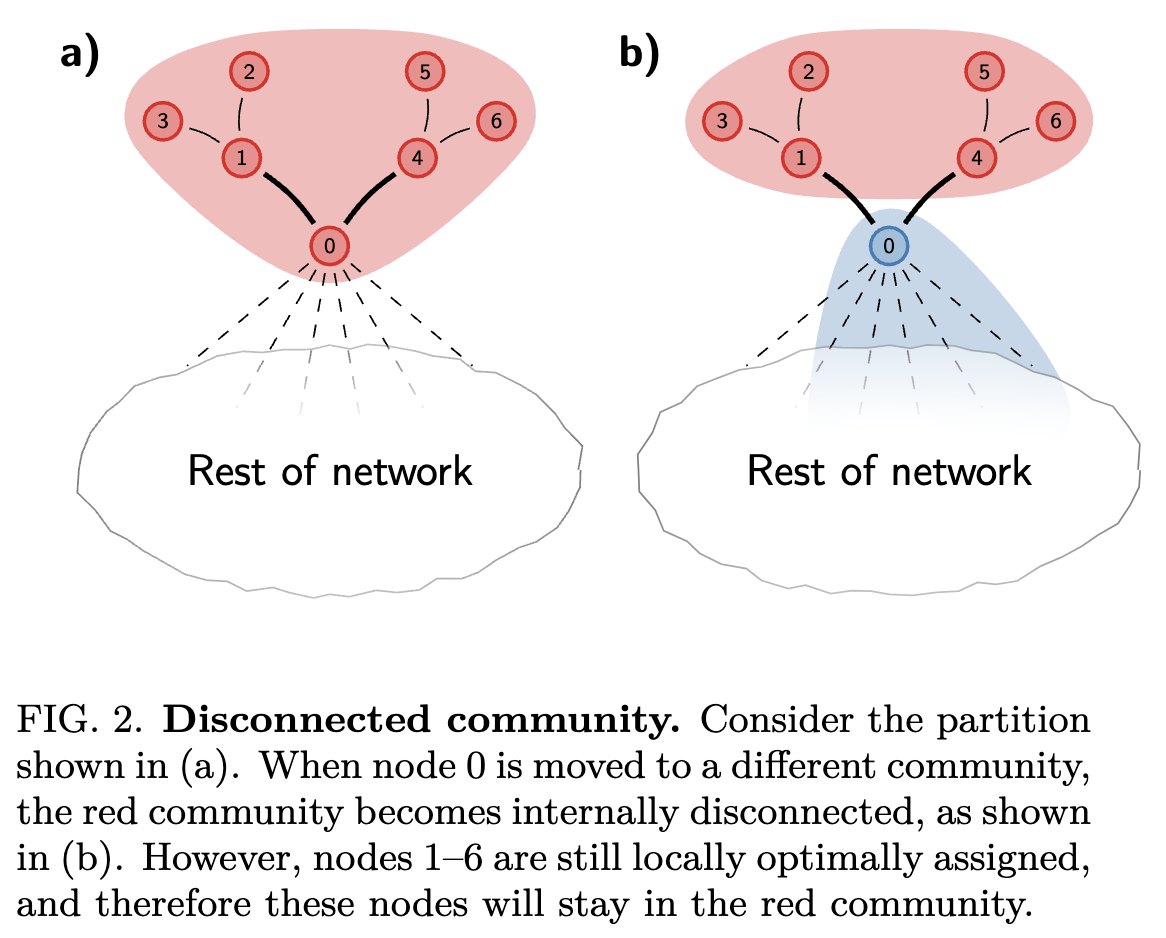
考虑论文图2的例子,图中更粗的边表示更强的连接性,更细的边表示更弱的连接性。在Louvain算法的计算过程中,可能会得到如图2(a)所示社区结构,节点0-6属于同一个社区,同时节点0与社区外其他很多点也有连接。随着Louvain算法的继续迭代,如果有足够多的节点0的在网络剩余部分的邻居节点构成了社区时,将节点0划到另一个社区可能是更优的,于是会造成图2(b)所示的情形,在这种情况下原来的社区就变成不连通的了。
上述例子是一个极端例子,除此之外,Louvain也有可能社区只是在非常弱的层面才是连通的。
Leiden原理
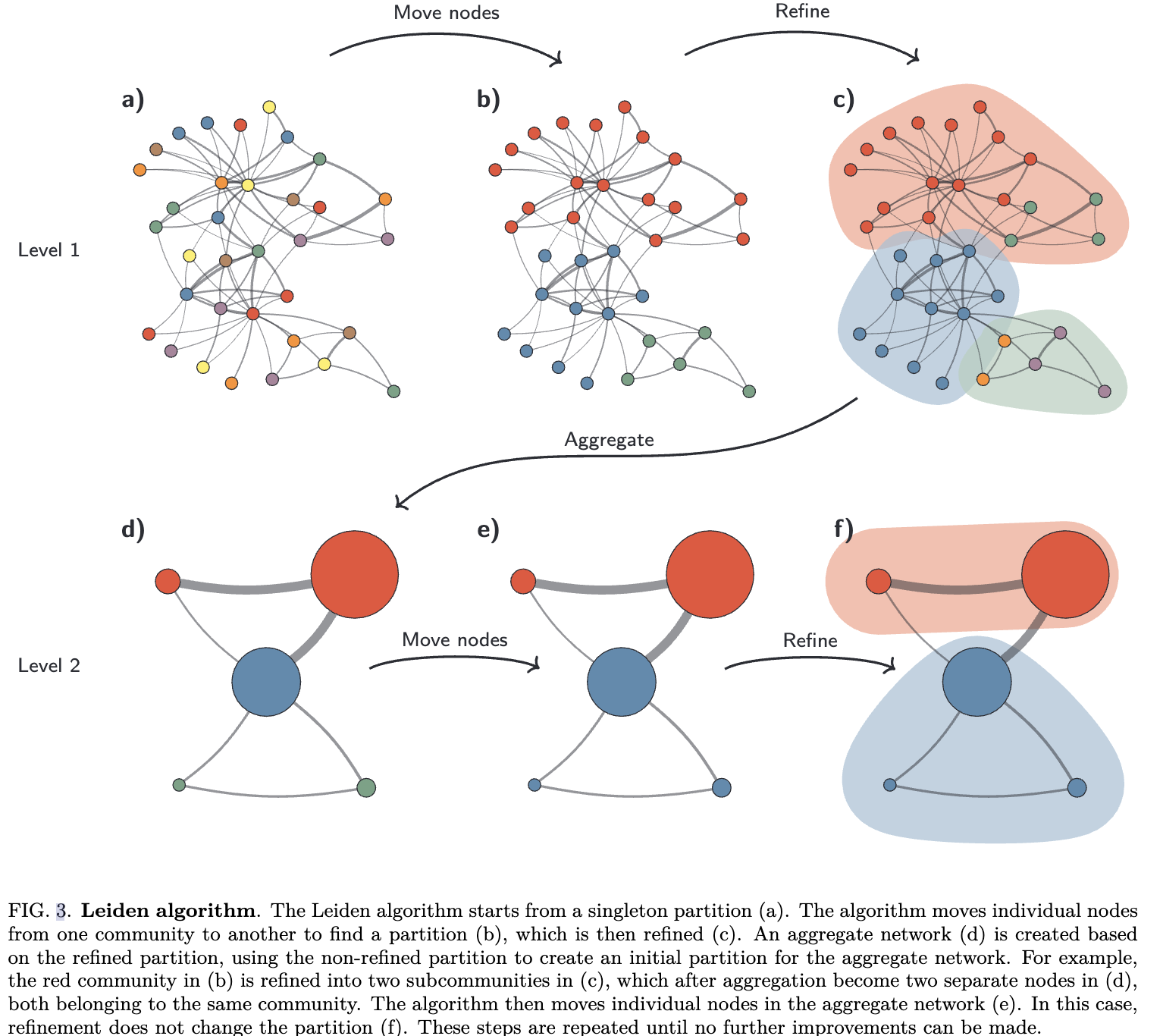
Leiden算法基于之前的几项工作来改进Louvain:smart local move algorithm, speeding up the local moving of nodes,moving nodes to random neighbours。它一共分为三个阶段:(1) 节点的局部移动(local moving of nodes),(2) 分区的细化(refinement of the partition),(3) 用第一步得到的未细化的分区创建聚合网络的初始分区,再基于细化分区得到最终的聚合网络。论文图3示意了Leiden算法,伪代码如论文A.2。这三个阶段不停地迭代得到最终的社区划分结果,与Louvain一样,得到的社区也是层次化社区。
第一阶段:节点的局部移动
在Louvain的第一阶段会不停地访问图中所有的节点直到没有节点可以移动到其他社区,而 Leiden算法使用快速局部移动流程(fast local move procedure),它只会访问那些其邻居改变了的节点,因此Leiden比Louvain更高效,其过程如下:
- 初始化一个包含网络中所有节点的队列,这些节点是被随机地添加到队列中的。
- 访问队列的第一个节点,如果将这个节点移动到其他社区中会使得质量函数得分增加,则将节点移动到新的社区,新社区为使得质量分增加最大的社区(伪代码17行)。
- 如果第二步的节点被移动到了新社区,遍历这个节点的邻居,将不属于节点的新社区且不在队列中的节点加入到队列的尾部。
- 重复2和3步直到队列为空。
第二阶段:分区的细化
在此阶段将第一步得到的分区 P \mathcal{P} P细化得到 P refined \mathcal{P}_{\text{refined}} Prefined,经过这一阶段后, P \mathcal{P} P中的一个社区有可能会被分成多个社区。其步骤如下:
- 细化分区 P refined \mathcal{P}_{\text{refined}} Prefined初始化时每一个节点表示一个社区。
- 将 P refined \mathcal{P}_{\text{refined}} Prefined中自己单独是一个社区的节点与其他社区进行合并,这个合并的规则有:a. 只能与分区 P \mathcal{P} P中相同社区的其他节点合并,b. 合并时的两个社区都必须是连通的(伪代码中的34行和37行)。
- 第2步中与其他社区合并时,不需要像第一阶段那样选择使得质量分数最大的社区进行合并,而是在满足质量分数大于0的社区中随机选择一个来合并,随机选择的概率是根据质量分来得到的,如伪代码38行。随机程度由参数 θ > 0 \theta>0 θ>0来决定,随机选择社区可使得分区空间更好的被探索。
关于伪代码中第34行理解(第37行是类似的), R = v ∣ v ∈ S , E ( v , S − v ) ≥ γ ∣ ∣ v ∣ ∣ ⋅ ( ∣ ∣ S ∣ ∣ − ∣ ∣ v ∣ ∣ ) R = {v | v ∈ S, E(v, S - v) ≥ γ ||v|| · (||S|| - ||v||)} R=v∣v∈S,E(v,S−v)≥γ∣∣v∣∣⋅(∣∣S∣∣−∣∣v∣∣)表示集合 S S S中的与集合内其他节点很好的连通(well-connected)的节点集合。 E ( v , S − v ) E(v,S-v) E(v,S−v)表示节点v与S中其他节点之间的边的数目, γ \gamma γ是分辨率,控制连通的程度, ∣ ∣ v ∣ ∣ ||v|| ∣∣v∣∣是节点v的度, ∣ ∣ S ∣ ∣ ||S|| ∣∣S∣∣是S中所有节点度数之和。
第三阶段:聚合网络,将第二步得到的细化分区得到聚合网络,因为细化分区是基于第一步得到的分区得到的,所以直接合并细化分区就可以了。
论文分析和证明了Leiden的一些保证,如论文表1所示。
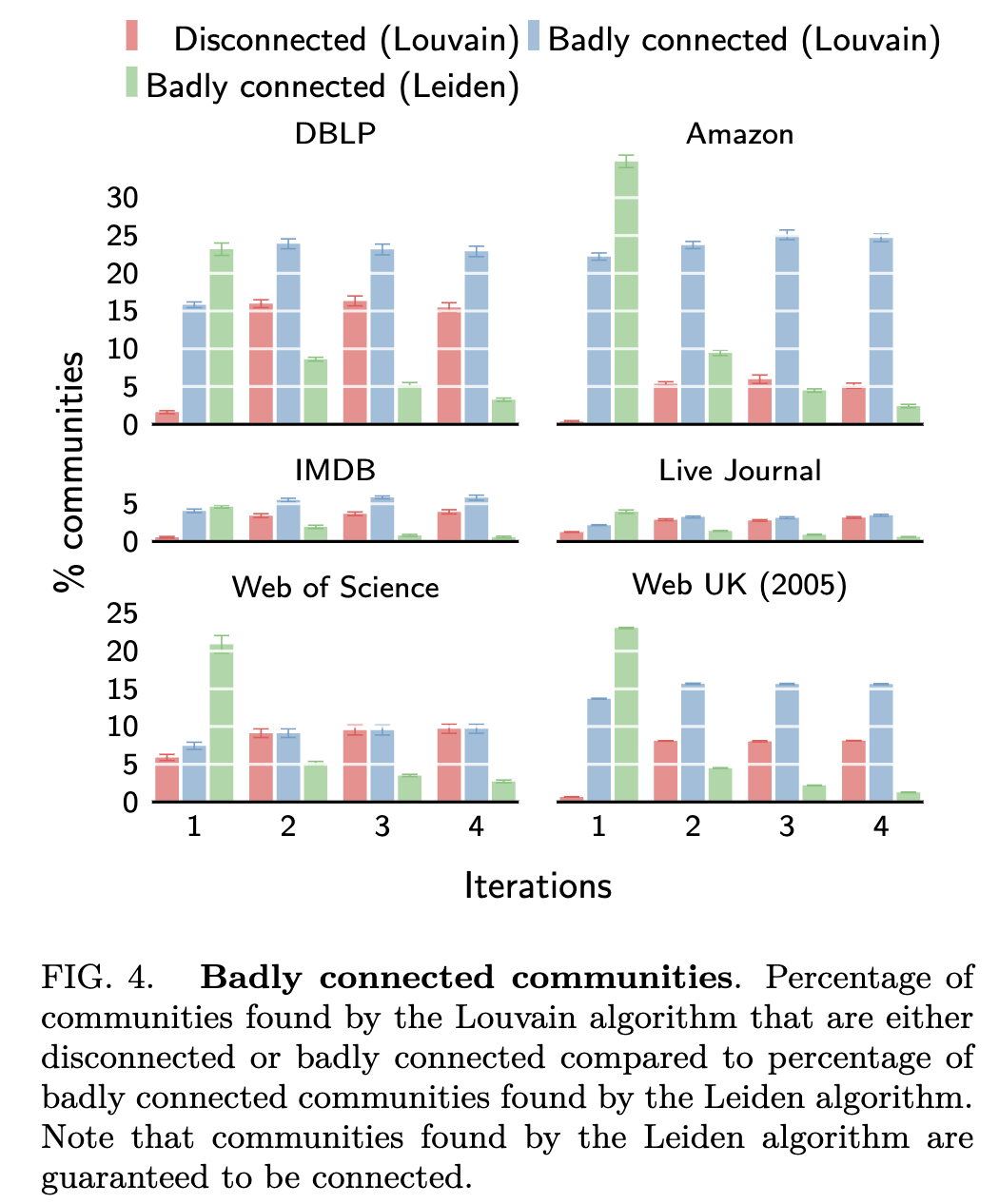
下图是比较Louvain和Leiden生成的社区连通差的实验比较结果,可以看到随着迭代的进行,Leiden可有效改善Louvain社区质量差的问题。
Leiden的实现
python库leidenalg是Leiden论文作者对Leiden的C++实现的python封装,算法本身是基于igraph和libleidenalg(用C++来实现)
import leidenalg
import igraph as ig
##创建Zachary karate club图
G = ig.Graph.Famous('Zachary')
## 基于模块度的社区发现
part = leidenalg.find_partition(G, leidenalg.ModularityVertexPartition)
python包graspologic也实现Leiden算法。
from graspologic.partition import hierarchical_leiden
import networkx as nx
seed = 123
max_cluster_size = 100
graph = nx.karate_club_graph()
## 参考自graphrag的代码
community_mapping = hierarchical_leiden(
graph, max_cluster_size=max_cluster_size, random_seed=seed
)
results: dict[int, dict[str, int]] = {}
for partition in community_mapping:
results[partition.level] = results.get(partition.level, {})
results[partition.level][partition.node] = partition.cluster