455.分发饼干(easy-自己想得出来并写好)
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
示例 1:输入: g = [1,2,3], s = [1,1] 输出: 1
解释: 你有三个孩子和两块小饼干,3个孩子的胃口值分别是:1,2,3。 虽然你有两块小饼干,由于他们的尺寸都是1,你只能让胃口值是1的孩子满足。 所以你应该输出1
思路:先将饼干大小和孩子的胃口大小都排序,再一一对比...需要注意的是for中的循环条件是饼干不是孩子,孩子加一的条件是前一个孩子得到满足之后,孩子的下标i才会加一!并且一旦这个孩子得到了满足,那么饼干的下标j和孩子的下标i均要直接加1进入下一次判断。所以才有了break语句!
代码如下:
class Solution {
public:
int findContentChildren(vector<int>& g, vector<int>& s) {
int g_len = g.size() ;
int s_len = s.size() ;
int i = 0 , j = 0 ,cnt = 0;
sort(g.begin(),g.end());
sort(s.begin(),s.end());
for(j ;j<s_len ;j++){
//当饼干满足孩子后,孩子才会加一
while((i<g_len) && (s[j]>=g[i])){
i++;
cnt++;
break ;//保证一块饼干只给一个孩子
}
}
return cnt ;
}
};435.无重叠区间(hard-自己没什么思路,写不了一点)
给定一个区间的集合 intervals ,其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量,使剩余区间互不重叠 。
示例 1:
输入: intervals = [[1,2],[2,3],[3,4],[1,3]] 输出: 1 解释: 移除 [1,3] 后,剩下的区间没有重叠。
示例 2:
输入: intervals = [ [1,2], [1,2], [1,2] ] 输出: 2 解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
示例 3:
输入: intervals = [ [1,2], [2,3] ] 输出: 0 解释: 你不需要移除任何区间,因为它们已经是无重叠的了。
思路:自己想了一下大概只能想到需要排序,因为这是一个区间,区间怎么排序呢,按照边界排序的话,排好了之后呢?又要怎么做呢?后面就不是很明了了。看了一下官方思路结合下面万能网友的评论大概理清楚了(直接贴一下评论区的某位网友回答,感觉比官方的更容易明白)
- 关于解法二贪心算法的合理性,这里作一下补充。其实这里的难点在于理解“为什么是按照右端点排序而不是左端点排序”。
- 官解里对这个描述的非常清楚了,这个题其实是
预定会议的一个问题,给你若干时间的会议,然后去预定会议,那么能够预定的最大的会议数量是多少?核心在于我们要找到最大不重叠区间的个数。 如果我们把本题的区间看成是会议,那么按照右端点排序,我们一定能够找到一个最先结束的会议,而这个会议一定是我们需要添加到最终结果的的首个会议。(这个不难贪心得到,因为这样能够给后面预留的时间更长)。 - 这里补充一下为什么不能按照区间左端点排序。同样地,我们把本题的
区间看成是会议,如果“按照左端点排序,我们一定能够找到一个最先开始的会议”,但是最先开始的会议,不一定最先结束。举个例子:
理清楚了算法的思路再进一步完成代码的编写,还是不太会,这个sort函数的用法,搜了一下感觉搜出来的都不太一样,有点迷惑,反正先整一份正确答案先。
这种情况是使用自定义比较函数对区间进行排序,然后自定义的比较函数cmp排序准则是,按照区间右端点的升序(a[1] < b[1])进行排序。因为题目中明确说了区间是一个长度为2的数组,所以索引只有0和1,索引0指示左端点,索引1指示右端点。======== 这样排序之后就可以按照上面的思路就行进一步操作了,排序后的第一个区间肯定是需要保留的,遍历后面的区间,留下与前面区间没有重合的即可。下面的代码定义的初始右端点是INT_MIN而不是第一个区间的右端点,道理是一样的。
class Solution {
public:
//std::sort 期望一个静态函数或一个函数对象
//故作为“自定义比较函数”应该定义为static类型
//根据题目,intervals是长度为2的数组,故索引只有0和1
static bool cmp(vector<int> &a, vector<int> &b){
return a[1] < b[1] ;
}
//vector<vector<int>>& intervals表明intervals是一个二维整数向量
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
int cnt = intervals.size() ;
sort(intervals.begin(), intervals.end(), cmp) ;
//使用 INT_MIN 宏来表示最小的 32 位整数值
int right = INT_MIN;
for(auto i :intervals){
//比较新intervals的左端点与当前intervals的右端点)(right)
//若左端点i[0]大于等于right,则新的intervals就不需要删除,同时更新right值
if(i[0]>=right){
right = i[1] ;
cnt--;
}
}
return cnt ;
}
};看了一下另外的解答方法:这里使用的是sort函数的默认排序方法,对于一维数组来说就是把数据按照升序排列好,但是对于区间来说,sort方法的默认排序是按照每个区间的第一个元素(起始位置)进行升序排序,如果起始位置的值是一样的,那么就按照第二个位置(结束位置)进行升序排序。
假设输入的二维数组(几个区间)为:intervals = {{1, 3}, {2, 2}, {3, 4}, {1, 2}},那么直接使用下面的sort函数进行排序,排列后的结果是intervals={{1, 2}, {1, 3} ,{2, 2}, {3, 4} }。
使用sort函数直接排序之后的进一步处理,没有第一种方法那么清晰明了,其实思路最后还是一样,都是需要不断更新区间的右端点,只是上一个右端点是按照升序拍好的,只需要看后一个区间和前一个有无重合就可以,现在这个需要自己来判断并更新右端点的值【因为排序可能会出现右端点的顺序是上面2324这样交错的】,需要理解一下,大概讲讲,意会一下:比如说你使用sort函数排序后得到了这样一组排序好的区间intervals={[1,5],[1,6],[2,3],[3,6],[4,7],[7,8]},按照代码,将排序后的第一个区间的右端点初始化为最小右端点,也就是right=5,然后从第二个区间开始遍历并更新right的值:
i=1时:intervals[1][0]=1 < right=5,表明第二个区间是和第一个区间有重合的,有重合就需要删除区间,所以cnt++,cnt=1,那删除哪个区间呢,根据上面的思想,需要删除右端点大的,保留右端点小的区间,所以就有了这句”right = min(right, intervals[i][1]);“此时right=5;
i=2时:intervals[2][0]=2 < right=5,表明第三个区间是和第二个区间有重合的,有重合就需要删除区间,所以cnt++,cnt=2,那删除哪个区间呢,根据上面的思想,需要删除右端点大的,保留右端点小的区间,所以此时right=3;
i=3时:intervals[3][0]=3 = right=3,表明第四个区间是和第三个区间是没有重合的,没有重合就要保留,就执行else中的语句,更新右端点的值,right=6,此时cnt还是等于2;
后面同理,不再赘述。最后的结果应该是,保留的区间是{[2,3],[3,6],[7,8]},cnt=3。画一个上面的那种线段区间图可以看得更清楚。
class Solution {
public:
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
int cnt = 0;
//这里排序默认是按照每个区间的第一个元素(起始位置)进行升序排序
//如果起始位置相同,则按第二个元素(结束位置)进行升序排序。
sort(intervals.begin(), intervals.end()) ;
//将排序后的第一个区间右端点初始化为最小的右端点
int right = intervals[0][1];
for (int i = 1; i < intervals.size(); i++) {
//判断当前区间的左端点是否小于上一个区间的右端点
//若小于 则需要删除,cnt++,同时更新
if (intervals[i][0] < right) {
cnt++;
right = min(right, intervals[i][1]);
} else {
right = intervals[i][1];
}
}
return cnt ;
}
};⭐关于sort函数:
std::sort 是 C++ 标准库中的一个函数,用于对指定范围内的元素进行排序。可以通过多种方式使用 std::sort,例如按照默认顺序排序,或者使用自定义的比较函数来排序。下面是几个使用示例:
① 按照默认(升序)顺序排序,该代码的输出是:1 2 3 5 7 8
#include <iostream>
#include <vector>
#include <algorithm>
int main() {
std::vector<int> nums = {5, 3, 8, 1, 2, 7};
std::sort(nums.begin(), nums.end());
for(int num : nums) {
std::cout << num << " ";
}
return 0;
}
② 按自定义顺序排序(降序),改代码的输出是:8 7 5 3 2 1
#include <iostream>
#include <vector>
#include <algorithm>
int main() {
std::vector<int> nums = {5, 3, 8, 1, 2, 7};
std::sort(nums.begin(), nums.end(), std::greater<int>());
for(int num : nums) {
std::cout << num << " ";
}
return 0;
}
③ 使用自定义比较函数排序,该代码的输出是:8 7 5 3 2 1
⭐ 关于这里为什么customCompare函数又不需要定义成静态的,不是很明白,GPT又说“std::sort 函数并不要求传入的自定义比较函数必须是静态函数”可是第一版本的代码中,如果不降传入的cmp函数定义成静态的话运行是会报错的
个人猜测,第一版代码中,cmp函数是定义在类中的,然而这里是一个普通全局函数,先这样记一下吧。
#include <iostream>
#include <vector>
#include <algorithm>
bool customCompare(int a, int b) {
return a > b; // 降序排序
}
int main() {
std::vector<int> nums = {5, 3, 8, 1, 2, 7};
std::sort(nums.begin(), nums.end(), customCompare);
for(int num : nums) {
std::cout << num << " ";
}
return 0;
}
④ 使用 Lambda 表达式排序,该代码的输出是:8 7 5 3 2 1
#include <iostream>
#include <vector>
#include <algorithm>
int main() {
std::vector<int> nums = {5, 3, 8, 1, 2, 7};
std::sort(nums.begin(), nums.end(), [](int a, int b) {
return a > b; // 降序排序
});
for(int num : nums) {
std::cout << num << " ";
}
return 0;
}
452.用最少数量的箭引爆气球(有思路-可写-一次过)
有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ,其中points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭,若有一个气球的直径的开始和结束坐标为 xstart,xend, 且满足 xstart ≤ x ≤ xend,则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后,可以无限地前进。给你一个数组 points ,返回引爆所有气球所必须射出的 最小 弓箭数 。
示例 1:
输入:points = [[10,16],[2,8],[1,6],[7,12]] 输出:2 解释:气球可以用2支箭来爆破: 在x = 6处射出箭,击破气球[2,8]和[1,6]。 在x = 11处发射箭,击破气球[10,16]和[7,12]。
思路 :这题和上一个越看越像,上一个求无重合区间的最大数量,这个看起来像是求重合区间的最大数量。不管怎么说,感觉还是需要将给定的区间排序的。想想看,怎么排序呢,我想的是直接用sort来排序,浅试一下。
可以,一下子就写出来了,不枉费我在上一个题花了那么长时间,泪目

class Solution {
public:
int findMinArrowShots(vector<vector<int>>& points) {
sort(points.begin(),points.end());
int len = points.size();
int left = points[0][0];
int right = points[0][1];
int cnt = points.size() ;
for(int i =1 ;i<len ;i++){
if(points[i][0] <= right){
//left = max(left,points[i][0]);
//不需要max语句,因为排好序的points[i][0]一定大于等于points[i-1][0]
left = points[i][0] ;
right = min(right,points[i][1]);
cnt--;
}else{
left = points[i][0] ;
right = points[i][1] ;
}
}
return cnt;
}
};用sort函数对区间进行排序后得到的就是,区间左端点升序,左端点相同的,右端点升序,这样一个数据。题目中要用最少的箭射中所有气球,我们假设开始需要射出的箭是气球的数量,也就是cnt = points.size(),然后再根据实际判断来减少箭的数量(cnt--);我们只需要维护一个区间就可以了,假设初始区间是points的第一个数据(排好序的!),找到其边界left和right,再看下一个区间(points[1])和第一个区间是否有交集:
如果没有交集,那第一个区间的气球就需要单独一只箭来击破;同时更新待维护区间 【left = points[i][0] ; right = points[i][1] ;】
如果有交集,那箭的数量就可以减一了(cnt--),同时需要求得其交集,在交集射出箭才能将两只气球都击破.left为什么不需要使用max语句更新,代码注释中有说。
406.根据身高重建队列(有点思路但是完全写不出来)
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示,第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[1] 是排在队列前面的人)
示例 1:
输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]] 输出:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 解释: 编号为 0 的人身高为 5 ,没有身高更高或者相同的人排在他前面。 编号为 1 的人身高为 7 ,没有身高更高或者相同的人排在他前面。 编号为 2 的人身高为 5 ,有 2 个身高更高或者相同的人排在他前面,即编号为 0 和 1 的人。 编号为 3 的人身高为 6 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。 编号为 4 的人身高为 4 ,有 4 个身高更高或者相同的人排在他前面,即编号为 0、1、2、3 的人。 编号为 5 的人身高为 7 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。 因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。
思路:有点没太看懂这题是要干什么,大概感觉是不是需要用到插入的方法,将第一个数据当作初始数据,然后后面就遍历所有数据并跟已经放好的数据进行比较,根据身高和排在前面的人数这两个已知条件来插入数据,最后得到一个符合数据属性的输出?感觉还是要排一下序比较好。🤔

会不了一点 给我看睡着了 等明天看看其他人的思路。
121.买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4] 输出:5 解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
思路:这个看起来比前面的要简单一点,至少题目一下子就能看懂了哈哈。
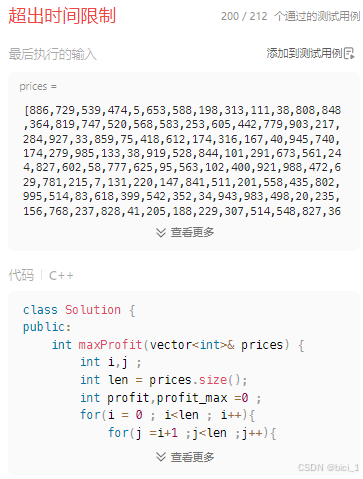
【暴力法】最简单粗暴的解法应该就是使用两个变量i.j遍历分别遍历所有数据,计算差值最大的,然后这个差值最大的就是最大利润(需要注意的是差值只能 后减前)。【如下所示,但是这种方法超时了!】
class Solution {
public:
int maxProfit(vector<int>& prices) {
int i,j ;
int len = prices.size();
int profit,profit_max =0 ;
for(i = 0 ; i<len ; i++){
for(j =i+1 ;j<len ;j++){
profit = prices[j]-prices[i] ;
profit_max = max(profit,profit_max);
}
}
return profit_max;
}
};虽然这个方法简单易懂,但是由于时间限制还是要需要另寻他法,这个是我看其他人的思路写的。大致意思就是,在遍历的过程中,不断更新股票价格的最低值并假设你是在那一天买入的【注意这里是更新股票价格的最低值而不是一下子就找到价格最低值!】,计算之后的价格与其的差值并返回最大差值。
例如:股票价格【7,2,5,1,6,4】
开始初始化minprice为7,profit_max为0;进入循环后,从第二个数据开始遍历,此时股票价格为2,那么更新minprice = 2,profit_max当然还是为0;执行i++,i的值为2,第三个数据是5,那么minprice还是2,此时profit_max更新为3;再之后i++,第四个数据是1,那么此时minprice就要进行一个更新,minprice=1,计算profit_max仍为3。以此类推可以得到最大的profit_max。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int minprice = prices[0];
int profit_max = 0;
int len = prices.size();
for(int i = 1 ;i<len;i++){
minprice = min(minprice , prices[i]);
profit_max = max(profit_max,prices[i]-minprice);
}
return profit_max;
}
};122.买卖股票的最佳时机Ⅱ(需要再看看 理解一下思路)
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。返回 你能获得的 最大 利润 。
示例 1:
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3。
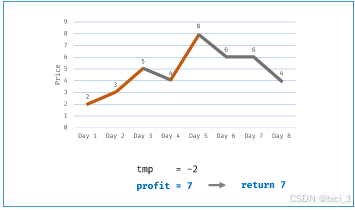
最大总利润为 4 + 3 = 7 。思路:遍历所有数据,运用贪心思想,所有数据上升段都认为是我们执行买卖得到的利润,将所有上升段相加就可以得到最大利润,遇到下降段则不理睬。
tmp是相邻两个数据间的差值,数据值上升则为正,下降则为负。
官方题解的图,原图是动图,看完还挺好理解的
class Solution {
public:
int maxProfit(vector<int>& prices) {
//贪心算法,就是把所有价格上升段都加上
int i,tmp ;
int len = prices.size();
int profit = 0;
for(i=1;i<len;i++){
tmp = prices[i]-prices[i-1] ;
if(tmp>0){
profit = profit + tmp ;
}
}
return profit ;
}
};官方还给了一种动态规划的思路,但是个人对动态规划这个思想不是很明白,感觉有点云里雾里,就没有细看。
605.种花问题(暴力解法很好理解)
假设有一个很长的花坛,一部分地块种植了花,另一部分却没有。可是,花不能种植在相邻的地块上,它们会争夺水源,两者都会死去。给你一个整数数组 flowerbed 表示花坛,由若干 0 和 1 组成,其中 0 表示没种植花,1 表示种植了花。另有一个数 n ,能否在不打破种植规则的情况下种入 n 朵花?能则返回 true ,不能则返回 false 。
思路:直接硬解,被自己蠢哭了,硬解也是可以的,就是要好好考虑一下边界以及数组大小为1和2的情况。
class Solution {
public:
bool canPlaceFlowers(vector<int>& flowerbed, int n) {
int len = flowerbed.size();
int cnt = 0;
if (len == 1) {
cnt = flowerbed[0]? 0:1 ;
} else if (len == 2) {
if (flowerbed[0] == 0 && flowerbed[1] == 0) {
cnt++;
}
} else {
for (int i = 0; i < len; i++) {
if (i == 0) {
if (flowerbed[i] == 0 && flowerbed[i + 1] == 0) {
flowerbed[i] = 1;
cnt++;
}
} else if (i == len - 1) {
if (flowerbed[i] == 0 && flowerbed[i - 1] == 0) {
flowerbed[i] = 1;
cnt++;
}
} else {
if (flowerbed[i - 1] == 0 && flowerbed[i + 1] == 0 &&
flowerbed[i] == 0) {
flowerbed[i] = 1;
cnt++;
}
}
}
}
return (cnt >= n);
}
};官方题解给的贪心算法思路,最后给了一个总结,看起来更简单一点,就是需要自己推一下间隙大小和能种花的数量之间的关系【为什么这样的就是贪心算法的思路了 不是很理解】
维护 prev 表示上一朵已经种植的花的下标位置,初始时 prev=−1,表示尚未遇到任何已经种植的花。
从左往右遍历数组 flowerbed,当遇到 flowerbed[i]=1 时根据 prev 和 i 的值计算上一个区间内可以种植花的最多数量,然后令 prev=i,继续遍历数组 flowerbed 剩下的元素。
遍历数组 flowerbed 结束后,根据数组 prev 和长度 m 的值计算最后一个区间内可以种植花的最多数量。
判断整个花坛内可以种入的花的最多数量是否大于或等于 n。
根据这个思路写出来的代码如下,这个思路就是要好好理解一下,左边界到第一次出现1之间可以种多少花,两个1之间可以种多少花,以及最后一个1到右边界之间可以种多少花,是有一些规律的。
class Solution {
public:
bool canPlaceFlowers(vector<int>& flowerbed, int n) {
int len = flowerbed.size();
int cnt = 0;
int pre = -1;
for(int i = 0;i<len;i++){
if(flowerbed[i] == 1){
if(pre < 0){
cnt = cnt + i/2 ;
}else{
cnt = cnt + (i-pre-2)/2 ;
}
pre = i ;
}
}
if(pre < 0){
//即遍历完整个数组都没有1,能种多少花
cnt = cnt + (len+1)/2 ;
}else{
//最后一个1出现之后,后面的0中还能种多少花
cnt =cnt + (len-pre-1)/2;
}
return (cnt >= n);
}
};392.判断子序列长度(和分饼干问题有点像,一遍过_easy)
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
进阶:
如果有大量输入的 S,称作 S1, S2, ... , Sk 其中 k >= 10亿,你需要依次检查它们是否为 T 的子序列。在这种情况下,你会怎样改变代码?
思路:这个题看起来和第455分饼干问题很像。注意外层循环条件是字符串t,字符串s的索引i加一的条件是找到了 t[j]等于s[i] 。
class Solution {
public:
bool isSubsequence(string s, string t) {
int slen = s.length() ;
int tlen = t.length() ;
int i=0, j=0,cnt=0;;
if(slen > tlen){
return false ;
}
//空字符串是任意字符串的子集
if(slen == 0){
return true ;
}
for(j = 0;j<tlen;j++){
if((s[i] == t[j]) && (i<slen)){
i++;
cnt++;
continue;
}
}
return cnt==slen ;
}
};看评论区有个网友写了个更简单的代码,附上。
class Solution {
public:
bool isSubsequence(string s, string t) {
int a = 0, b = 0;
while (a < s.size() && b < t.size())
if (s[a] == t[b++])
a++;
return a == s.size();
}
};
665.非递减数列(需再看_如何对递减段的数据进行删除)
给你一个长度为 n 的整数数组 nums ,请你判断在 最多 改变 1 个元素的情况下,该数组能否变成一个非递减数列。我们是这样定义一个非递减数列的: 对于数组中任意的 i (0 <= i <= n-2),总满足 nums[i] <= nums[i + 1]。
思路:这个题目看起来似曾相识。我想的是原数组至多只能存在一个下降段,否则的话只删除一个是不能够将其变为非递减数列的。再结合一下网友的思路,找到递减段了,那么如何对递减段的数据进行删除呢,是删除nums[i]还是删除nums[i-1]。
class Solution {
public:
bool checkPossibility(vector<int>& nums) {
int len = nums.size();
int cnt = 0;
for(int i = 1; i<len; i++){
//直接找出现递减的地方
if(nums[i] < nums[i - 1]){
cnt++ ;
if (i == 1 || nums[i] >= nums[i - 2]) {
nums[i - 1] = nums[i];//相当于删除nums[i-1]这个数据
} else {
nums[i] = nums[i - 1];
//相当于删除nums[i]这个数据
//例如 3 4 2 nums[i]=2我判断得到nums[i] < nums[i - 1]
//如果删除 nums[i - 1]即删除4的话,nums[i - 2]还是小于nums[i]=2的
//所以需要删除nums[i]
}
}
}
return cnt<=1 ;
}
};53.最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组是数组中的一个连续部分。