1.缺失值的处理
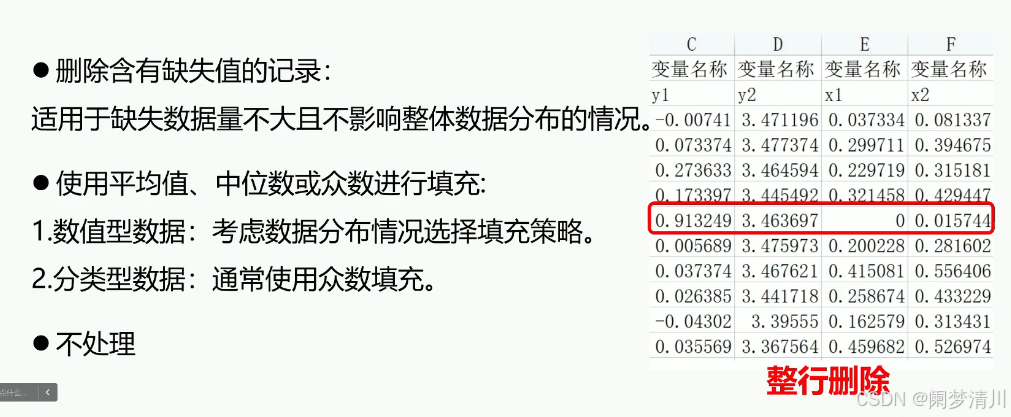
(1)像在下面的这个表格里面,这个对于缺失的数据,我们需要分情况进行分析,如果这个数据就是一个数值型的数据,我们可以使用平均值进行处理;
(2)对于这个分类型数据,就是比如一个问题,你想要吃香蕉,苹果,还是梨,对于这个问题,要求我们必须要选择一个,这个时候,我们就可以依据这个大家的喜好程度,把这个众数作为这个填充值,这个时候是合理的;
(3)有些时候,如果我们有理由去说明这个数据的不存在是合理的,这个时候我们就可以不去处理这个缺失的数据;
2.异常值的处理
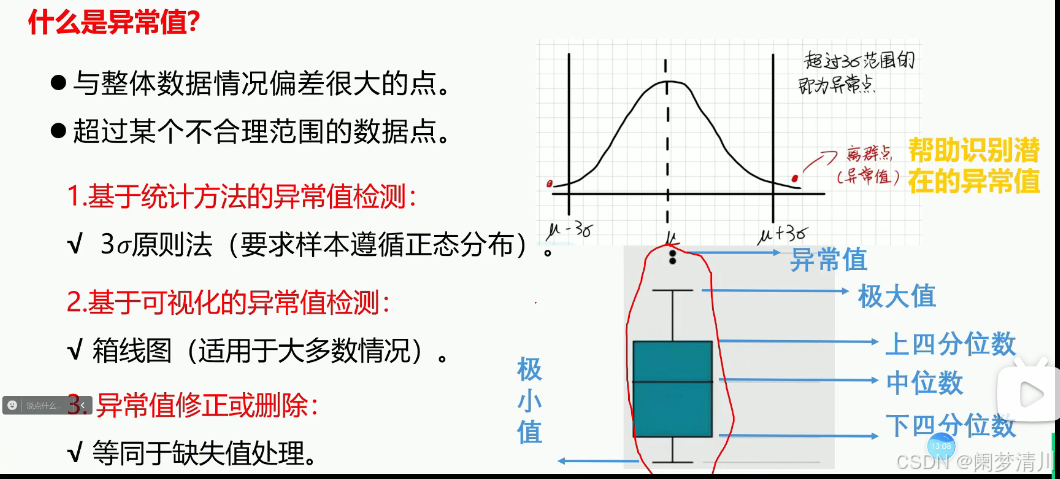
(1)对于这个异常值,我们可以使用正态分布的3西格玛原则进行检验,在这个μ+3西格玛之外的,我们就称之为异常值;
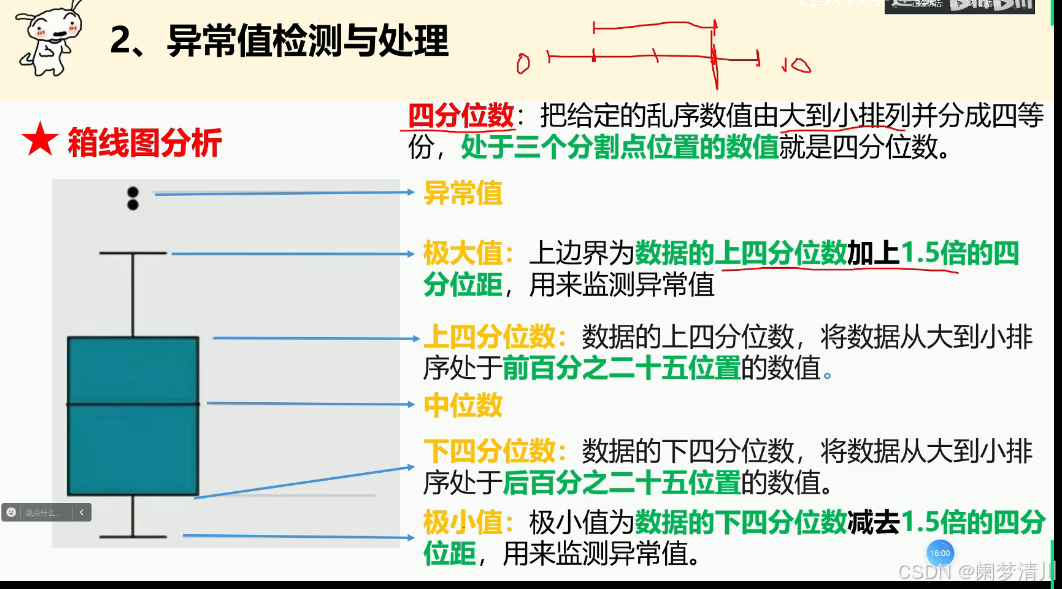
(2)对于这个箱线图,包括上面的两个孤立的数据点,我们把这个孤立的点就叫做异常值,上面的线就是极大值,下面的线就是极小值;
(3)对于这个异常值的处理方法,我们可以等同于这个缺失值的处理;
(4)箱型图(箱线图)的说明介绍
这个箱型图就是需要知道一个叫做分位数的东西,这个有上四分位数,下四分位数,这个4是因为我们把这个所有的区间划分为了4份,例如这个0~10的数据,我们生成4份,就是0~2.5,2.5~5,5~7.5,7.5~10,这个5就是中位数,这个是毋庸置疑的,但是这个上四分位数就是7.5,下四分位数就是2.5.仅此而已;
3.赛题分析--神经网络算法
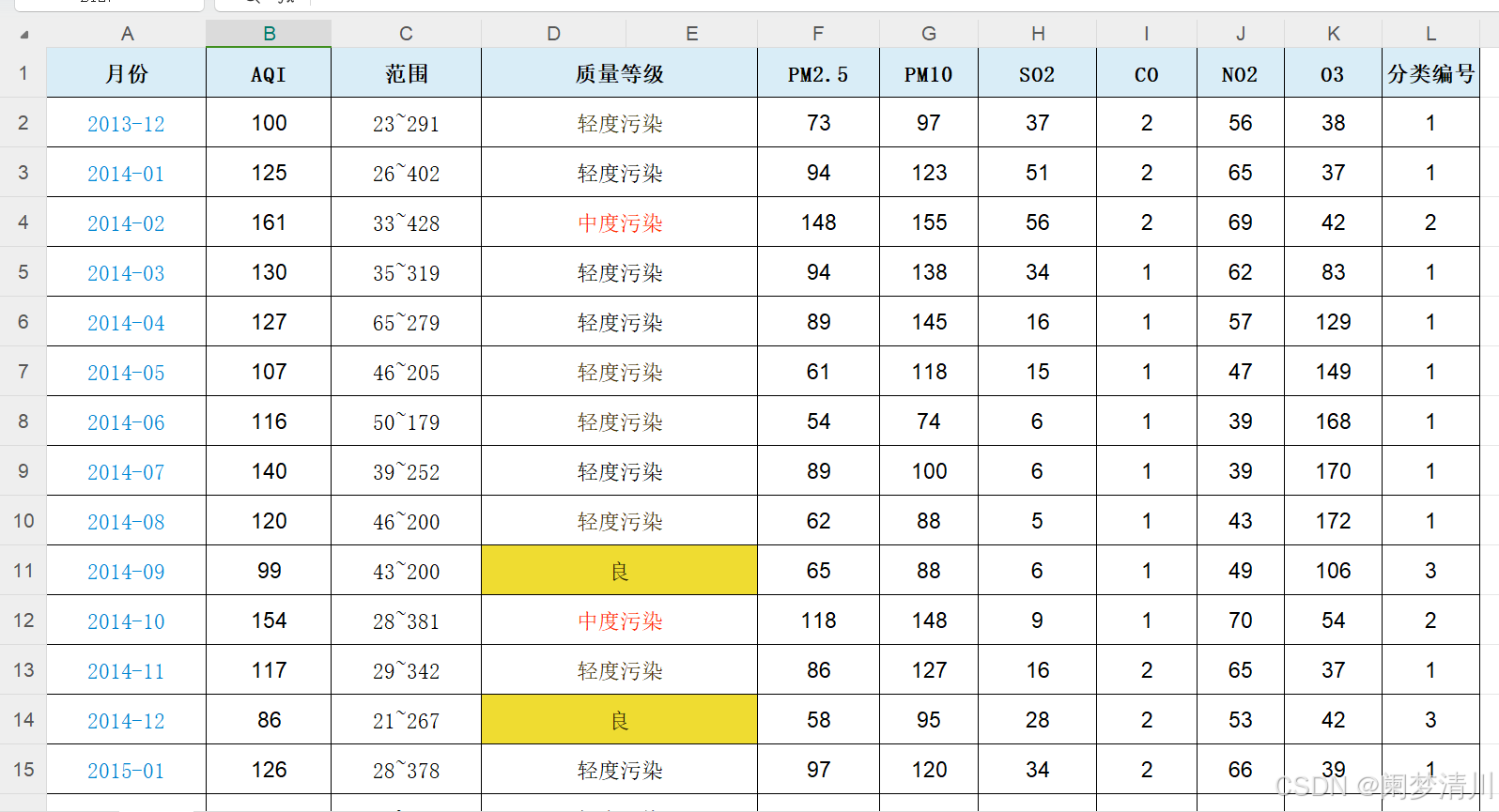
(1)这个题目大概是要干什么,我们需要做什么,这个就是我们首先需要搞明白的,我在这个下面放了一张图片,这个里面就是让我们去探讨这个AQI(可以用来衡量空气质量的一种指标),我们想要探讨这个指标和PM2.5 PM10 SO2 CO NO2 O3这些物质的含量有没有关系,我们是否可以根据这个物质含量去预测这个AQI指标;
(2)我们在预测的时候使用到了下面的这个第一种数据处理的方法,就是数据的Min-Max规范化处理方法;因为这个神经网络需要分为这个数据集和训练集,以及这个相关的层,感兴趣的可以根据这个案例下去自主学习,
(3)我之前在我的主页专栏python人工智能有相关的介绍,但是还是浅显的,我自己对于这个方面也不是很了解,同学们可以自行学习,我也是第一次在这个matlab上面去运行这个代码,很多地方不是很了解,还是需要学习的,同学们可以自己下去学习;
(4)下面有这个源代码,前提这个需要有数据,但是这个数据是excel形式的,我在这个博客里面没有办法导入进来,想使用这个案例以及相关数据的小伙伴可以私信我,我觉得这个案例还是值得研究的;
%%问题:
% 有一组北京空气质量数据,通过数据中空气中的各成分含量(PM2.5,PM10,SO2,
% CO,NO,O3)预测空气评价指标AQI值。
%% 清空环境变量
warning off
clc;
clear;
close all;
%% 导入数据
date=xlsread("北京空气质量数据(1).xlsx");
%% 划分训练集和测试集
date1=randperm(126);
% date1=double(1:126);
P_train=date(date1(1:90),5:10)';
T_train=date(date1(1:90),1)';
M=size(P_train,2); %返回行向量数
P_test=date(date1(91:end),5:10)';
T_test=date(date1(91:end),1)';
N=size(P_test,2);
%% 数据归一化
[P_train,ps_input]=mapminmax(P_train,0,1); %将最小值和最大值映射到[0,1]
P_test=mapminmax("apply",P_test,ps_input);
[~,ps_output]=mapminmax(T_train,0,1);
t_test=mapminmax("apply",T_test,ps_output);
%% 数据平铺
P_train=double(reshape(P_train,6,1,1,M));%将数据切割为6×1
P_test=double(reshape(P_test,6,1,1,N));
t_train=T_train';
t_test=t_test';
%% 数据格式转换(元胞数组)
p_train=cell(M,1);
for i=1:M
p_train(i,1)=num2cell(P_train(:,:,1,i),1);
end
p_test=cell(N,1);
for i=1:N
p_test(i,1)=num2cell(P_test(:,:,1,i),1);
end
%% 创建模型
layers=[
sequenceInputLayer(6) % 建立输入层
lstmLayer(4,"OutputMode","last") % LSTM层
reluLayer % Relu激活层
fullyConnectedLayer(1) % 全连接层
regressionLayer]; % 回归层
%% 参数设置
options=trainingOptions("adam",... % adam 梯度下降法
"MiniBatchSize",15,... % 批大小
"MaxEpochs",2000,... % 最大迭代次数
"InitialLearnRate",8e-2,... % 初始学习率
"LearnRateSchedule","piecewise" ,... % 学效率下降
"LearnRateDropFactor",0.08,... % 学效率下降因子
"LearnRateDropPeriod",1000,... % 经过1000次训练后
"Shuffle","every-epoch",... % 每次训练打乱数据集
"Plots","training-progress",... % 画出曲线
"Verbose",false);
%% 训练模型
net=trainNetwork(p_train,t_train,layers,options);
%% 仿真测试
t_sim1=predict(net,p_train);
t_sim2=predict(net,p_test );
%% 格式转换(double)
t_sim1=double(t_sim1);
t_sim2=double(t_sim2);
%% 数据反归一化
T_sim1=mapminmax("reverse",t_sim1,ps_output);
T_sim2=mapminmax("reverse",t_sim2,ps_output);
%% 均方根误差
error1=sqrt(sum((t_sim1'-t_train).^2)./M);
error2=sqrt(sum((t_sim2'-t_train).^2)./N);
%% 查看网络结构
analyzeNetwork(net)
%% 相关指标计算
% R
R1=1-norm(T_train-t_sim1')^2/norm(T_train-mean(T_train))^2;
R2=1-norm(T_test-t_sim2)^2/norm(T_test-mean(T_test))^2;
disp("训练集数据R2:", num2str(R1));
disp("训练集数据R2:", num2str(R2));
%% MAE
mae1=sum(abs(t_sim1'-T_train)./M);
mae2=sum(abs(t_sim2-T_train)./N);
disp(["训练集数据的MAE:",num2str(mae1)]);
disp(["训练集数据的MAE:",num2str(mae2)]);
%% MBE
mbe1=sum(t_sim1'-T_train)./M;
mbe2=sum(t_sim2-T_test)./N;
disp(["训练集数据的MBE:", num2str(mbe1)]);
disp(["训练集数据的MBE:", num2str(mbe2)]);
%% 绘图
figure
plot(1:M,T_train,"r-*",1:M,t_sim1,"b-o","LineWidth",1)
legend("真实值","预测值")
xlabel("预测样本")
ylabel("预测结果")
grid
figure
plot(1:N,t_sim2,"b-o","LineWidth",1)
legend("预测值")
xlabel("预测样本")
ylabel("预测结果")
grid