目录
1.聚类分析步骤
1.1简单介绍
K-Means聚类分析是属于聚类分析的一种,这个数据机器学习的算法;
对数据进行自动分组,使得同一组内的数据样本尽可能相似,不同组之间的数据样本尽可能不同,以此来完成用户细分,这就是聚类。
K-Means是非监督学习中一种很经典的聚类算法。
K代表类别数量,Means代表每个类别内的均值,所以K-Means算法又称为K-均值算法。
1.2两个概念
该算法会根据数据样本间的相似性,将数据样本自动分为K个簇(cluster),相似的数据样本会尽可能被聚到一个簇内。簇,指的就是类别或是组。
每个簇都有一个中心位置/中心点,被称作为质心(centroid)。
- 最开始,会先从数据集中随机选取K=2个对象作为初始的质心。
- 剩余待分类的样本数据就可以评估自己和哪个质心最相似,然后加入到该质心代表的簇里即可。
1.3几种距离
1.4更新质心
- 由于一开始的质心是随机选择的,导致结果也存在一定的随机性。
- 因此,当所有样本点分配完成后,需要重新计算2个簇的质心。
- 计算方式是计算每个簇内所有样本的均值。
- 如果此时计算出的均值和之前的初始质心不一样,就要使用该均值更新这个簇的质心。这就是K-Means算法又称为K均值算法的原因。
1.5终止条件
更新这个质心之后,我们需要不断地进行这个求解距离和计算均值的过程,不断的进行重复,我们通常会设置一个最小值,当质心的位置变化小于该值时,就停止。
或者我们自己设置这个迭代的次数,达到这个最大迭代次数就停止;
2.归一化处理
我们这个聚类分析是为了解决这个RFM模型的遗留问题,就是这个RFM进行这个划分的时候是使用的这个数据分箱的操作,回顾一下,就是根据这个等级进行划分,我们给定这个需要进行划分的区间个数,确定这个具体每一个区间的范围,这个时候我们的这个数据分箱就完成了,但是这个数据分箱有局限性,我们使用聚类进行这个过程的优化;
我们下面的这三个特征向量的差距比较大,因此我们进行归一化处理,这个有公式,但是我们理解即可,我们直接使用这个python里面的模块进行计算即可;
1. 导入模块:从sklearn.preprocessing模块中导入用于归一化的
StandardScaler类;2. 实例化:创建一个StandardScaler对象,不需要传入参数;
3. 数据归一化:调用StandardScaler对象中的
fit_transform()函数,对x进行归一化。
# 导入pandas模块,简称pd
import pandas as pd
'''读取数据集并获取特征变量'''
# 读取文件,并赋值给变量df
df = pd.read_csv("/Users/user_info/new_user_info.csv")
# 获取特征变量x
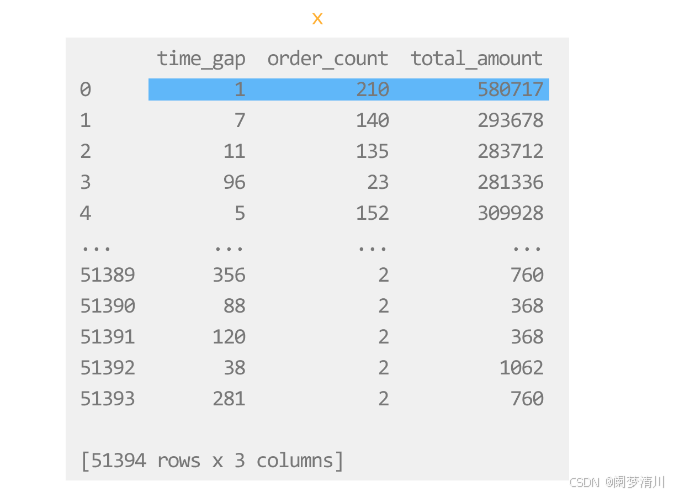
x = df[["time_gap","order_count","total_amount"]]
'''数据归一化'''
# TODO 导入sklearn.preprocessing模块中的StandardScaler类
from sklearn.preprocessing import StandardScaler
# TODO 创建一个StandardScaler对象,并赋值给变量scaler
scaler = StandardScaler()
# TODO 调用scaler中的fit_transform()函数,对x进行归一化,并赋值给变量x_scale
x_scale = scaler.fit_transform(x)
# TODO 输出x_scale进行查看
print(x_scale)3.肘部法则
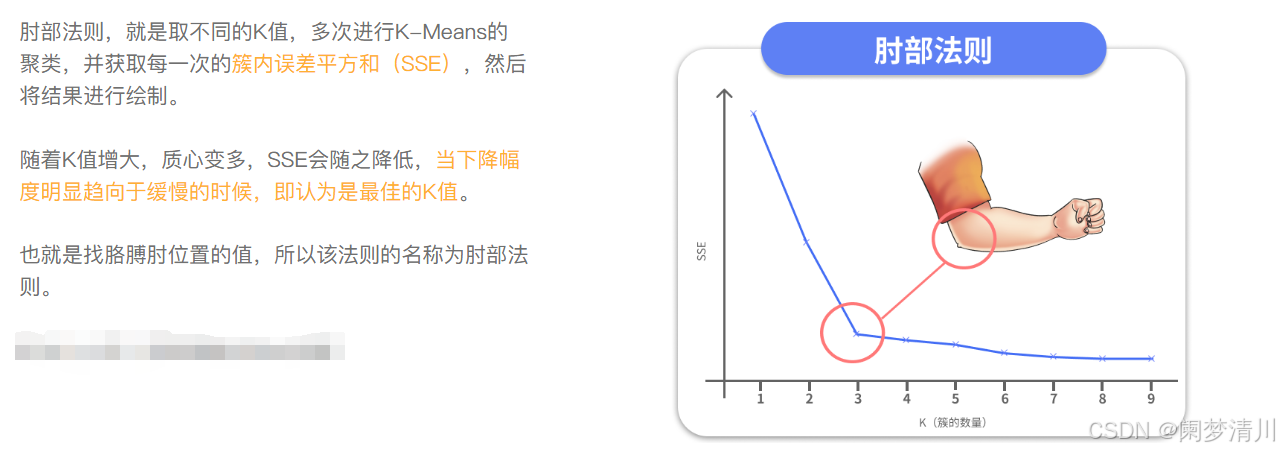
我们之前是把这个PRM模型分成了8个部分,2*2*2=8,但是这个划分的结果不一定科学,到底划分为几个类别最合适,这个时候我们可以借助这个肘部法则确定我们的k值;
4.搭建K-Means分析模型
下面这个搭建模型的步骤就是:
- STEP1. 导入模型
- STEP2. 初始化模型,设置参数
- STEP3. 训练模型
- STEP4. 获取结果
# 导入pandas模块,简称pd
import pandas as pd
'''读取数据集并获取特征变量'''
# 读取文件,并赋值给变量df
df = pd.read_csv("/Users/user_info/new_user_info.csv")
# 获取特征变量x
x = df[["time_gap","order_count","total_amount"]]
'''数据归一化'''
# 导入StandardScaler类
from sklearn.preprocessing import StandardScaler
# 创建一个StandardScaler对象
scaler = StandardScaler()
# 对x进行归一化
x_scale = scaler.fit_transform(x)
# 将x_scale从二维数组转换为DataFrame
x_scale = pd.DataFrame(x_scale, columns=x.columns, index=x.index)
'''搭建K-Means模型'''
# 导入sklearn.cluster模块中的KMeans模型
from sklearn.cluster import KMeans
# 使用KMeans()初始化模型
# 设置参数n_clusters=3,,表示的就是聚类的数量就是3
# random_state=1保证程序每一次运行的效果都是一样的
# 将结果赋值给model
model = KMeans(n_clusters=3, random_state=1)
# 使用fit()函数训练模型
model.fit(x_scale)
# 获取聚类后的质心
print(f"质心:{model.cluster_centers_}")
# 获取每个样本所属的簇
print(f"标签:{model.labels_}")
# 获取SSE,误差平方和
print(f"SSE:{model.inertia_}")5.选择最佳K值
STEP1.导入KMeans模型;
STEP2.创建一个空列表sseList,用于存储每次的SSE;
STEP3.取不同的K值,本例中我们取1至9,多次进行K-Means的聚类;
STEP4.获取当前的SSE,并使用append()函数将其添加到sseList中;
STEP5.在for循环外,输出sseList;
STEP6.绘制折线图展现结果,设置K值为x轴,sseList为y轴,marker为"o"。
# 导入pandas模块,简称pd
import pandas as pd
'''读取数据集并获取特征变量'''
# 读取文件,并赋值给变量df
df = pd.read_csv("/Users/user_info/new_user_info.csv")
# 获取特征变量x
x = df[["time_gap","order_count","total_amount"]]
'''数据归一化'''
# 导入sklearn.preprocessing模块中的StandardScaler类
from sklearn.preprocessing import StandardScaler
# 创建一个StandardScaler对象
scaler = StandardScaler()
# 对x进行归一化
x_scale = scaler.fit_transform(x)
'''获取最佳K值'''
# TODO 导入sklearn.cluster模块中的KMeans模型
from sklearn.cluster import KMeans
# TODO 创建一个空列表,用于存储每次的簇内误差平方和(SSE)
sseList = []
# TODO 使用for循环,取K值为1至9
for K in range(1,10):
# TODO 使用KMeans()初始化模型
# 设置参数n_clusters=k, random_state=1
# 将结果赋值给model
model = KMeans(n_clusters=K, random_state=1)
# TODO 使用fit()函数训练模型
model.fit(x_scale)
# TODO 通过.inertia_属性获取SSE,并添加到sseList中
sseList.append(model.inertia_)
# TODO 输出sseList
print(sseList)
# TODO 导入matplotlib.pyplot,并使用"plt"作为该模块的简写
import matplotlib.pyplot as plt
# TODO 使用plt.plot()函数
# 以K的取值为x轴的值,sseList为y轴的值
# 设置marker="o",绘制折线图
plt.plot(range(1,10),sseList,marker="o")
# TODO 展示图像
plt.show()通过可视化结果结合这个肘部法则,我们可以看到这个最佳的k=3,接下来我们使用这个k=3进行分析;
6.绘制3D图形
# 导入pandas模块,简称pd
import pandas as pd
'''读取数据集并获取特征变量'''
# 读取文件,并赋值给变量df
df = pd.read_csv("/Users/user_info/new_user_info.csv")
# 获取特征变量x
x = df[["time_gap","order_count","total_amount"]]
'''数据归一化'''
# 导入sklearn.preprocessing模块中的StandardScaler类
from sklearn.preprocessing import StandardScaler
# 创建一个StandardScaler对象
scaler = StandardScaler()
# 对x进行归一化
x_scale = scaler.fit_transform(x)
'''进行KMeans算法的聚类运算'''
# 导入sklearn.cluster模块中的KMeans模型
from sklearn.cluster import KMeans
# 使用KMeans()初始化模型
# 设置参数n_clusters=3, random_state=1
# 将结果赋值给model
model = KMeans(n_clusters=3, random_state=1)
# 使用fit()函数训练模型
model.fit(x_scale)
# 获取每个样本所属的簇
labels = model.labels_
'''可视化结果'''
# 导入matplotlib.pyplot,并使用"plt"作为该模块的简写
import matplotlib.pyplot as plt
# 从mpl_toolkits.mplot3d中导入Axes3D类
from mpl_toolkits.mplot3d import Axes3D
# 通过 rcParams 参数将字体设置为 Arial Unicode MS
plt.rcParams["font.sans-serif"] = "Arial Unicode MS"
# 使用plt.figure()函数创建画布
# 添加参数figsize设置画布大小为(12,8)
fig = plt.figure(figsize=(12,8))
# 创建3D坐标轴对象
ax = fig.add_subplot(projection="3d")
# 设置散点颜色
color = ["dodgerblue", "seagreen", "lightcoral"]
# 遍历三个簇
for i in range(0,3):
# 获取分类为i的点
d = x[labels == i]
# 绘制分类为i的簇所对应的R、F和M这三个指标数据
ax.scatter(d["time_gap"], d["order_count"], d["total_amount"], color=color[i], label=f"用户群体{i}")
# 设置x轴标题为"R"
ax.set_xlabel("R")
# 设置y轴标题为"F"
ax.set_ylabel("F")
# 设置z轴标题为"M"
ax.set_zlabel("M")
# 使用plt.legend()函数展示图例
plt.legend()
# 展示图像
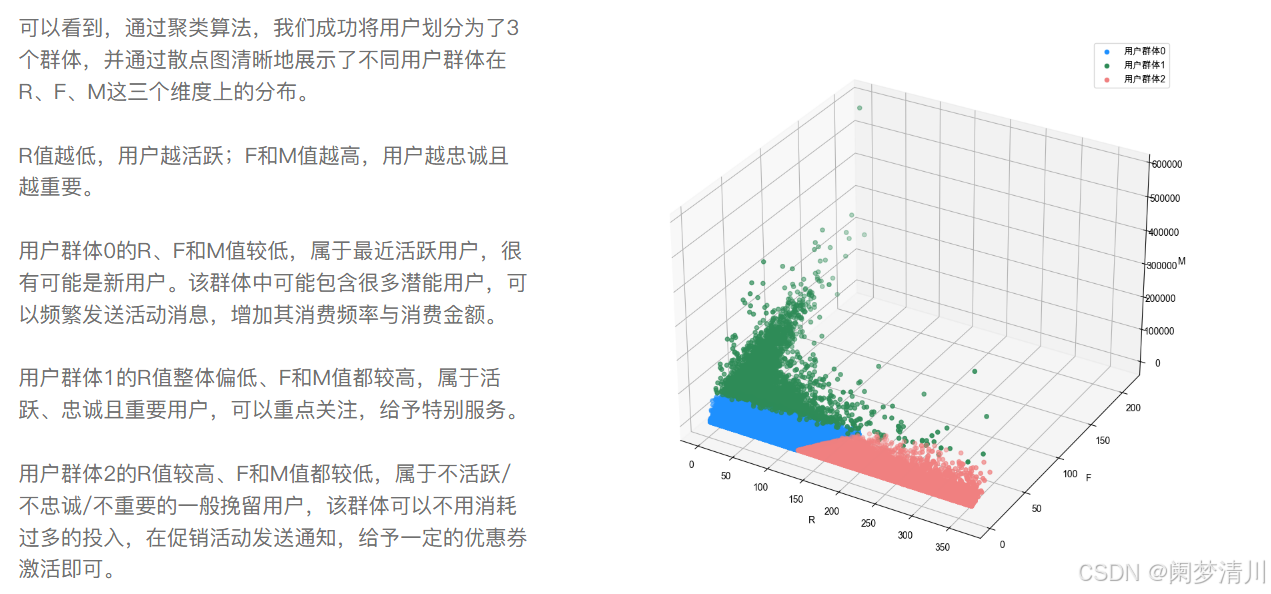
plt.show()根据这个绘制的结果结合我们的题目进行说明即可: