提示：以下是本篇文章正文内容

一、题目

输入一个 n
行 m
列的整数矩阵，再输入 q
个询问，每个询问包含四个整数 x1,y1,x2,y2
，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式
第一行包含三个整数 n，m，q
。

接下来 n
行，每行包含 m
个整数，表示整数矩阵。

接下来 q
行，每行包含四个整数 x1,y1,x2,y2
，表示一组询问。

输出格式
共 q
行，每行输出一个询问的结果。

数据范围
1≤n,m≤1000
,
1≤q≤200000
,
1≤x1≤x2≤n
,
1≤y1≤y2≤m
,
−1000≤矩阵内元素的值≤1000

输入样例：
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
输出样例：
17
27
21

二、思路及代码

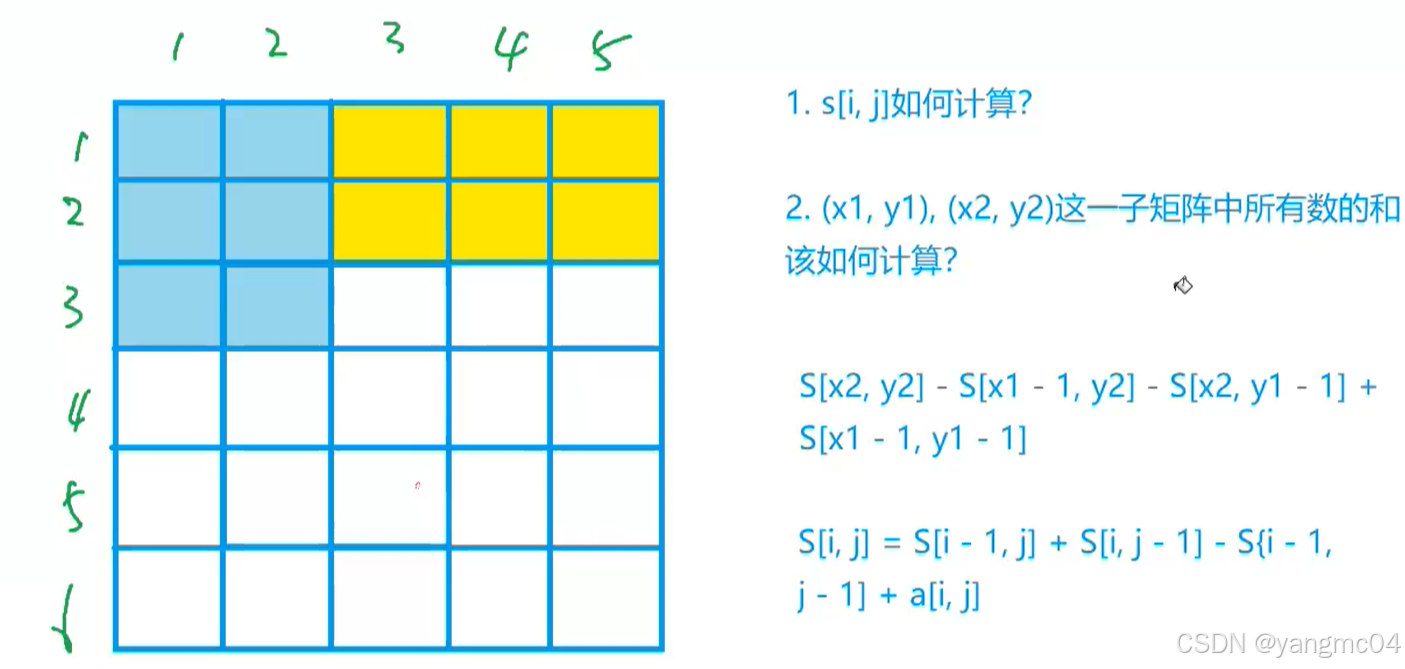
1.思路

2.答案

代码如下：

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;


const int N = 1010;

int a[N][N], s[N][N];

int main()
{
    int n, m, q;
    cin >> n >> m >> q;
    
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++)
            cin >> a[i][j];
    
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++)
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
    
    while (q --)
    {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        
        cout << s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1] << endl;
    }
    
    return 0;
}

总结

Just Review.