CVPR-2019

1 Background and Motivation

目前主流的目标检测算法，在优化 bbox regression 分支时采用的 loss 为 $l1$（ Faster RCNN 的 smooth L1） or $l2$ （YOLO ）范数 loss

然而 there is a gap between optimizing the commonly used distance losses for regressing the parameters of a bounding box（l1 or l2 范数） and maximizing this metric value（基于 IoU 体系下的 mAP）.

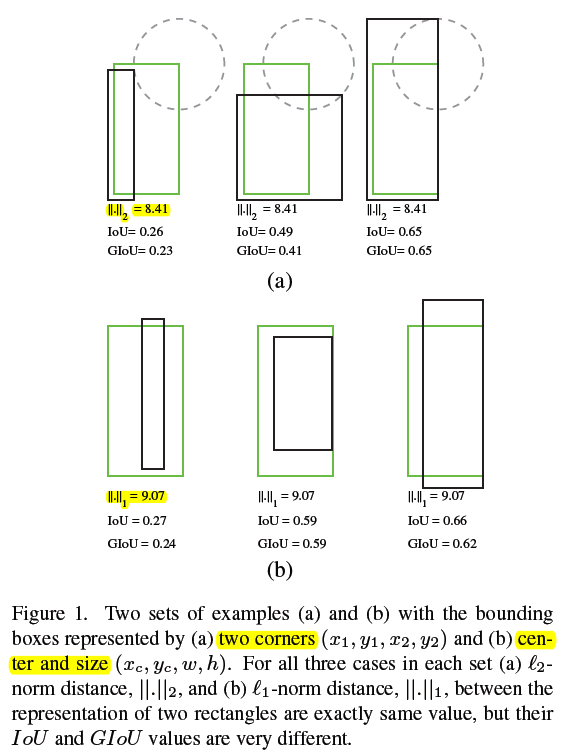
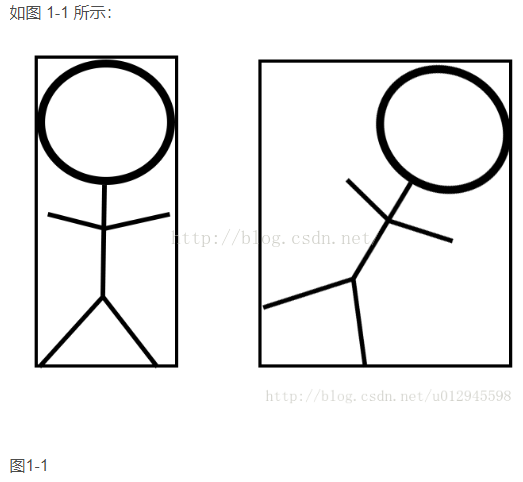
例如下图（a）中 3 种相交情况下，prediction（黑色） 到 GT（绿色） 右上角位置的 L2 范数（$\sqrt{(x_g-x_p{)}^2+(y_g-y_p{)}^2}=R$）虽然相等（同理，也可以在 GT 其它 3 个角画圆以保证其它 3 个角 prediction 和 GT 的 L2 范数相同，进而确保不同相交情况下 4 个角的 L2 范数相同），但是 IoU 大相径庭

下图（b）是 3 种相交情况下，prediction 和 GT 中心坐标的 L1 范数（$|x_p-x_g|+|y_p-y_g|$ = R）相等，但 IoU 各有千秋

The optimal objective for a metric is the metric itself

也即可以直接用 IoU 作为 loss（1-IoU） 来优化 bbox regression 分支，但存在如下瑕疵

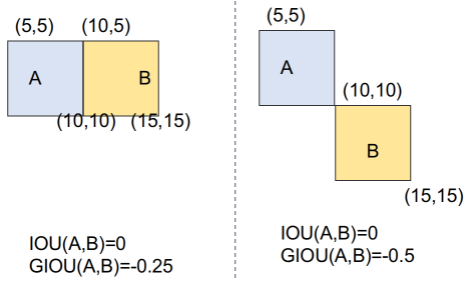
1）prediction 与 GT 不相交时，IoU 为 0 ，无法衡量二者距离远近

图片来自 IOU & GIOU & DIOU 介绍及其代码实现

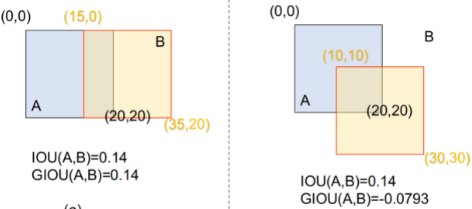
2）prediction 与 GT 相交时，也无法衡量相交情况

图片来自 IOU & GIOU & DIOU 介绍及其代码实现

本文针对 IoU Loss 的上述缺点进行改进，提出了 Generalized Intersection over Union（GIoU）

2 Related Work

• Object detection accuracy measures：mAP50 for VOC / mAP for COCO
• Bounding box representations and losses：l1 l2 loss, IoU loss
• Optimizing IoU using an approximate or a surrogate function

3 Advantages

改进目标检测任务中回归分支的 loss，提出 IoU Loss 优化版的 GIoU Loss

GIoU loss 替换掉现有主流目标检测器中 bbox regression 分支上的 loss，效果取得了一致性的提升

4 Generalized Intersection over Union

IoU two appealing features：

• IoU as a distance
• IoU is invariant to the scale of the problem

缺点：

• 不相交时，IoU 统为 0 ，无法衡量二者距离远近
• 相交时，无法辨别具体相交情况

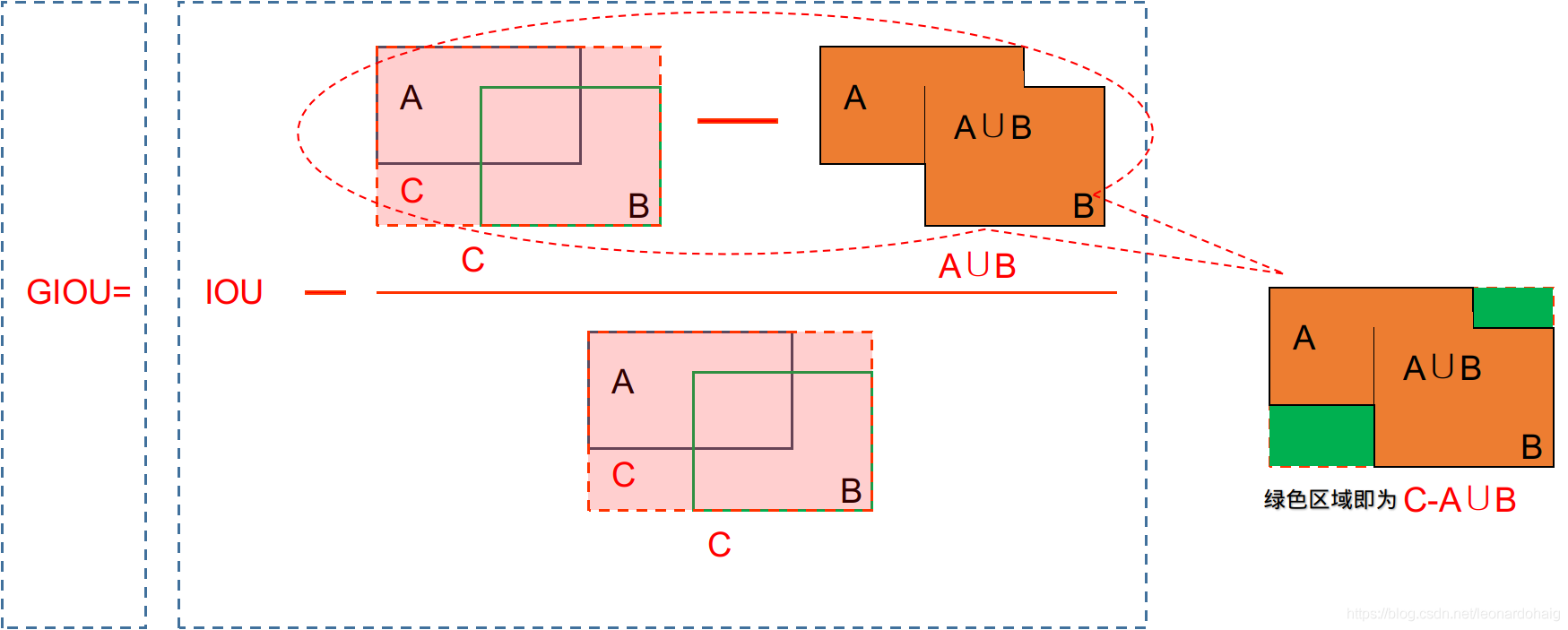
IoU 改进版 GIoU

图片来自 IOU & GIOU & DIOU 介绍及其代码实现

其中 C 是包含 A 与 B 的最小 convex shapes（例如 A 和 B 为矩形框的话，C 也即矩形框，A 和 B 为椭圆的话，C 也即椭圆）
S 可以理解为所有 convex shapes 的集合

C \ (A U B) 也即 C - (A U B)

性质：

• GIoU as a distance（同 IoU）
• invariant to the scale of the problem（同 IoU）
• a lower bound for IoU，∀A,B ⊆ S GIoU(A,B) ≤ IoU(A,B)，${\lim }_{A\to B}$ GIoU(A,B) = IoU(A,B)
• ∀A,B ⊆ S, −1 ≤ GIoU(A,B) ≤ 1.
  $$\underset{\frac{|A\cup B|}{|C|}\to 0}{\lim }GIoU(A,B)=-1$$
  $$|A\cup B|=|A\cap B|时，GIoU=IoU=1$$

4.1 GIoU as Loss for Bounding Box Regression

back-propagating min, max and piece-wise linear functions, e.g. Relu, are feasible

当 IoU = 0 时， $L_{GIoU}$ 也能发挥作用

$$L_{GIoU}=1-GIoU=1+\frac{A^C-u}{A^C}-IoU=1+\frac{A^C-u}{A^C}=2-\frac{u}{A^C}$$

其中$A^C$ 表示 BBox $B^p$ 和 BBox $B^g$ 最小闭包 C 的 area

最小化 $L_{GIoU}$ 相当于最大化 $\frac{u}{A^c}$，也即最大化分子 $u=A^p+A^g$（IoU 为 0 时是定值），最小化分母 $A^C$，这样一来就会拉近 $B^p$ 和 $B^g$ 的距离，朝着 IoU 不为 0 的方向优化，有意思！

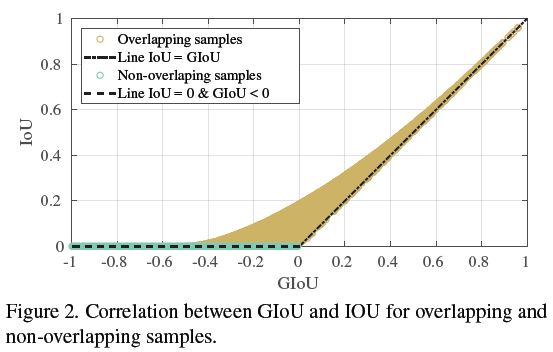
这个图可以看到不相交时，GIoU 还是有值的，而 IoU 恒为 0
相交时，GIoU 可能为负，而 IoU 都大于 0

5 Experiments

5.1 Datasets

• PASCAL VOC
• MS COCO

5.2 YOLO v3

DarkNet-608， MSE bbox regression loss

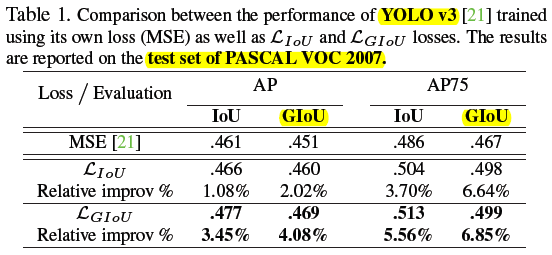
1）PASCAL VOC 2007

上表中 AP 下方 GIoU 表示用 GIoU 替换 IoU 来计算得分配合设定的 threshold 卡正负样本

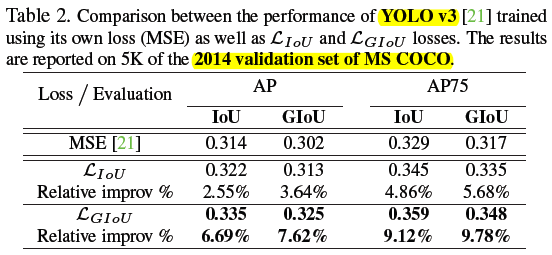
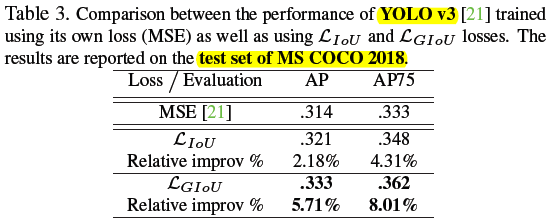
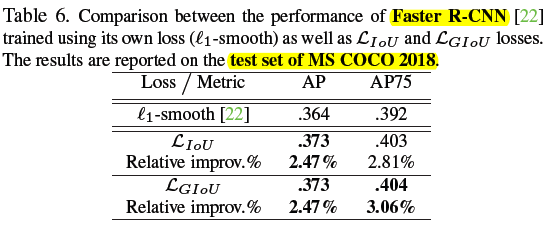
2）MS COCO


Table3 中为啥不用 GIoU 卡阈值了？是因为 test set 的 GT 没公开，只能提交用默认的 IoU 测试

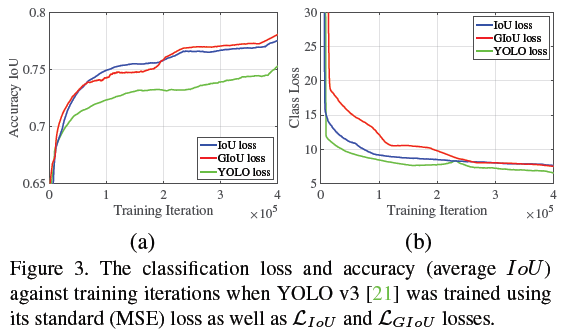
上图可以看出，IoU loss 系列的 location acc 明显提升，但是 class loss 并不是降到最低的

作者给出的解释是 the results can be further improved with a better search for regularization parameters

这个 regularization parameters 我猜测是平衡 cls loss 和 reg loss 的系数

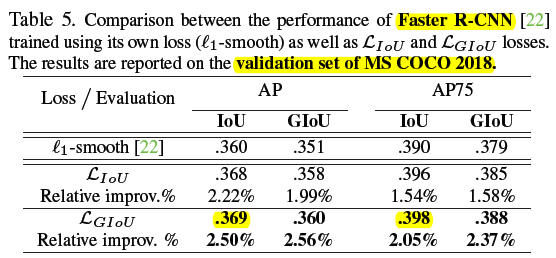
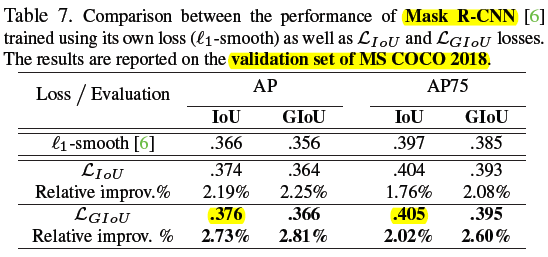
5.3 Faster RCNN and Mask RCNN

backbone 是 resnet 50，bbox regression loss 仅替换 second stage

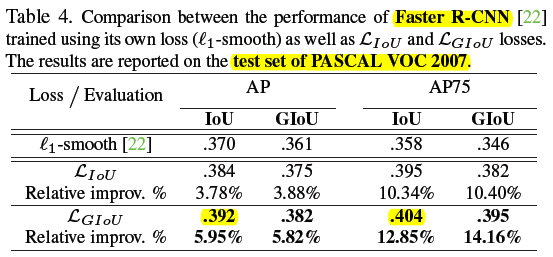
1）PASCAL VOC 2007

IoU thresholds (并不是 GIoU) + GIoU Loss 最猛

2）MS COCO

和 VOC 数据集反应的现象一样，IoU thresholds (并不是 GIoU) + GIoU Loss 最猛

作者的解释为

• the detection anchor boxes on Faster R-CNN and Mask R-CNN are more dense than YOLO v3, resulting in less frequent scenarios where LGIoU has an advantage over LIoU such as non-overlapping bounding boxes.（这个持怀疑态度，GIoU 仅用在 second stage，anchor 数量是不及 YOLOv3 的，前者 1000~2000 个，后者 3 个 scale ，每个 scale HxWx3 个）

• the bounding box regularization parameter has been naively tuned on PASCAL VOC, leading to sub-optimal result on MS COCO（VOC 也不见你 GIoU 比 IoU 猛啊）

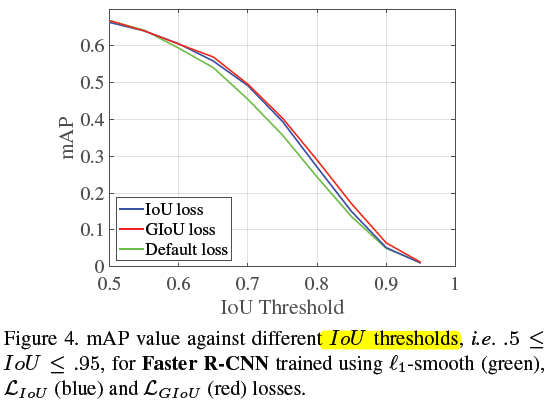
最后看看效果图

这个图真的是看了个寂寞

IoU 相比 L1-smooth 提升还是可以的，GIoU 和 IoU 之间区别不太大

6 Conclusion（own）

• BBox regression：to alleviate scale sensitivity of the representation, the bounding box size offsets are defined in log-space
• ℓ1-smooth in Faster /Mask-RCNN and MSE in YOLO v3
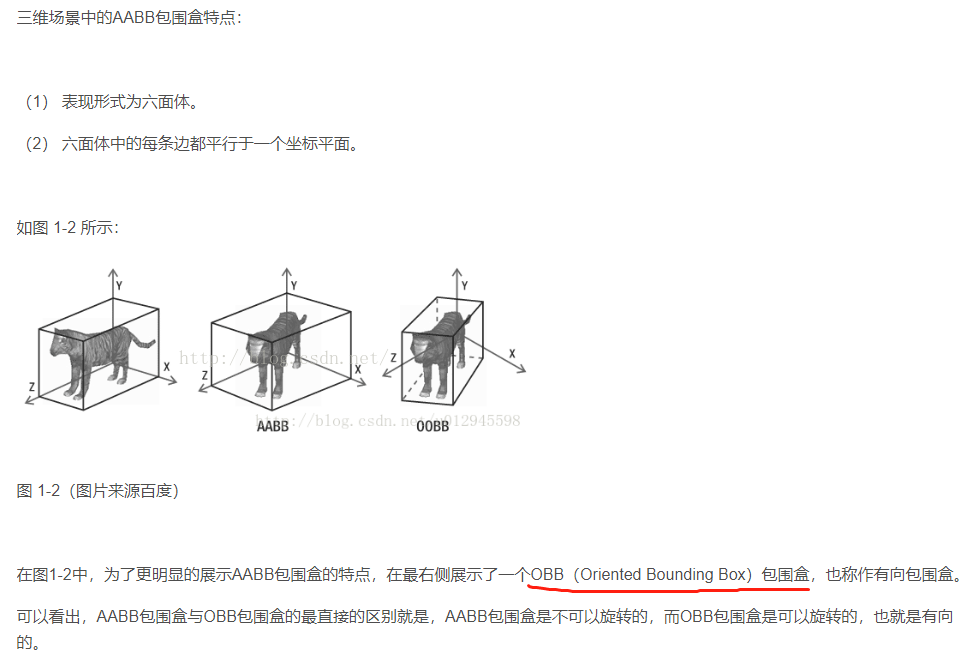
• two axis-aligned rectangles（参考 AABB(axis-aligned bounding box)）