3.1.1_栈的基本概念
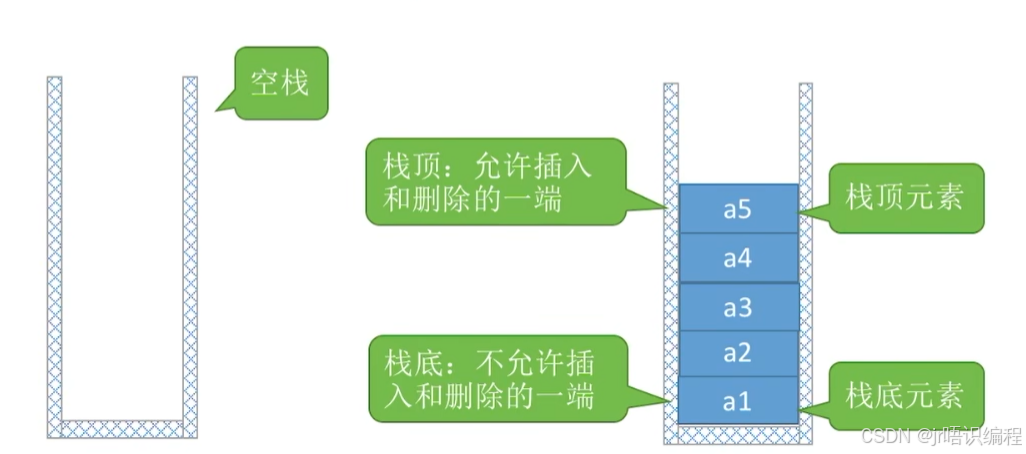
栈(Stack)是只允许在一端进行插入或删除操作的线性表
重要术语“栈顶、栈底、空栈
进栈顺序:
a1->a2->a3->a4->a5
出栈顺序:
a5->a4->a3->a2->a1
特点:后进先出
Last In First Out(LIFO)
逻辑结构:与普通线性表相同
数据的运算:插入、删除操作有区别
栈的基本操作:
InitStack(&S):初始化栈。构造一个空栈S,分配内存空间。
DestoryStack(&L):销毁栈。销毁并释放栈S所占用的内存空间。
Push(&S,x):进栈,若栈S未满,则将x加入使之成为新栈顶。
Pop(&S,&x):出栈,若栈S非空,则弹出栈顶元素,并用x返回。
GetTop(S,&x):读栈顶元素。若栈S非空,则用x返回栈顶元素。
其他常用操作:
StackEmpty(S):判断一个栈S是否为空。若S为空,则返回true,否则返回false。
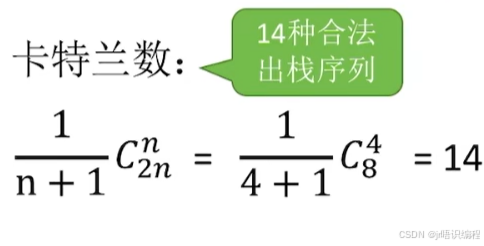
栈的常考题型:
进栈顺序:
a->b->c->d->e
有哪些合法的出栈顺序?
3.1.2_栈的顺序存储实现
顺序栈的定义
#define MaxSize 10 //定义栈中元素的最大个数
typedef struct{
ElemType daya[MaxSize]; //静态数组存放栈中元素
int top; //栈顶指针
} SqStack;
void testStack(){
SqStack S; //声明一个顺序栈(分配空间)
//后续操作
}顺序存储:给各个数据元素分配连续的存储空间,大小为MaxSize*sizeof(ElemType)
初始化操作:
//初始化栈
void InitStack(SqStack &S){
S.top=-1; //初始化栈顶指针
}
//判断栈空
bool StackEmpty(SqStack S){
if(S.top==-1) //栈空
return true;
else //不空
return false;
}进栈操作:
//新元素入栈
bool Push(SqStack &S, ElemType x){
if(S.top==MaxSize-1) //栈满,报错
return false;
S.top = S.top +1; //指针加一
S.data[S.top]=x; //新元素入栈
return true;
}出栈操作:
//出栈操作
bool Pop(SqStcak &S,ElemType &x){
if(S.top==-1) //栈空,报错
return false;
x=S.data[S.top]; //栈顶元素先出栈
S.top=S.top-1; //指针再减1
return true;
}数据还残留在内存中,只是逻辑上被删除了
另一种方式也可以让top指针开始设为0
顺序栈的缺点:栈的大小不可变
共享栈:两个栈共享同一片空间
顺序存储,用静态数组实现,并需要记录栈顶指针
3.1.3_栈的链式存储实现
链栈的定义:
typedef struct Linknode{
ElemType data; //数据域
struct Linknode *next; //指针域
} *LiStack; //栈类型定义进栈/出栈都只能在栈顶一端进行(链头作为栈顶)
3.2.1_队列的基本概念
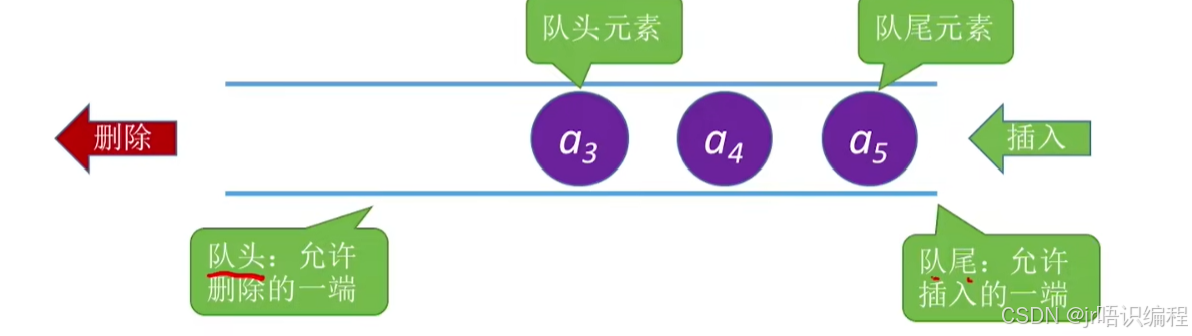
队列(Queue)是只允许在一端进行插入,在另一端删除的线性表
入队:在一端进行插入
出队:在另一端删除
特点:先进入队,列的元素先出队
重要术语:队头、队尾、空队列
队列的特点:先进先出
First In First Out(FIFO)
队列的基本操作:
InitQueue(&Q):初始化队列,构造一个空队列Q。
DestoryQueue(&Q):销毁队列。销毁并释放队列Q所占用的内存空间。
EnQueue(&Q,x):入队,若队列Q未满,将x加入,使之成为新的队尾。
DeQueue(&Q,&x):出队,若队列Q非空,删除队头元素,并用x返回。
GetHead(Q,&x):读队头元素,若队列Q非空,则将队头元素赋值给x。
其他常用操作:
QueueEmpty(Q):判队列空,若队列Q为空返回true,否则返回false。
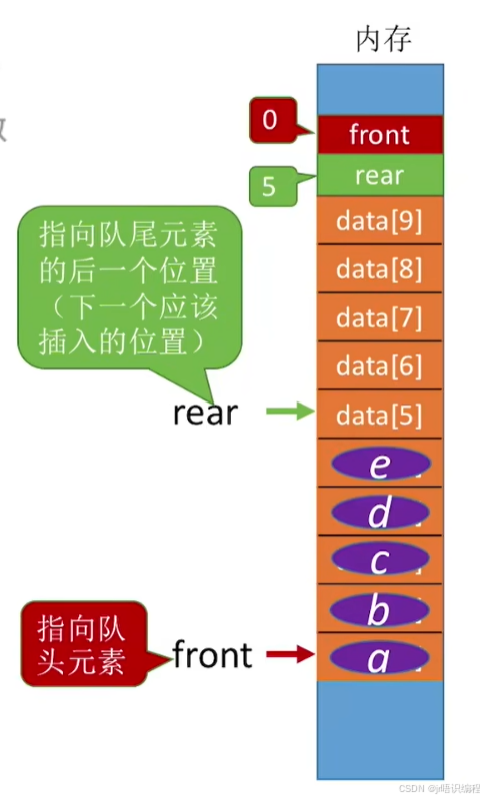
3.2.2_队列的顺序实现
#define MaxiSize 10 //定义队列中元素的最大个数
typedef struct{
ElemType data[MaxSize]; //用静态数组存放队列元素
int front,rear; //队头指针和队尾指针
}SqQueue;
void testQueue(){
SqQueue Q; //声明一个队列(顺序存储)
//后续操作
}初始化操作:
//初始化队列
void InitQueue(SqQueue &Q){
//初始时 队头、队尾指针指向0
Q.rear=Q.front=0;
}
void testQueue(){
//声明一个队列(顺序存储)
SqQueue Q;
InitQueue(Q);
//后续操作
}//判断队列是否为空
bool QueueEmpty(SqQueue Q){
if(Q.rear==Q.front) //队空条件
return true;
else
return false;
}入队操作(只能从队尾入队)
//入队
bool EnQueue(SqQueue &Q,ElemType x){
if(队列已满)
return false; //队满则报错
Q.data[Q.rear]=x; //将x插入队尾
Q.rear=(Q.rear+1)%MaxSize; //队尾指针加一去模
return true;
}a%b==a除以b的余数
在《数论》中,通常表示为a MOD b
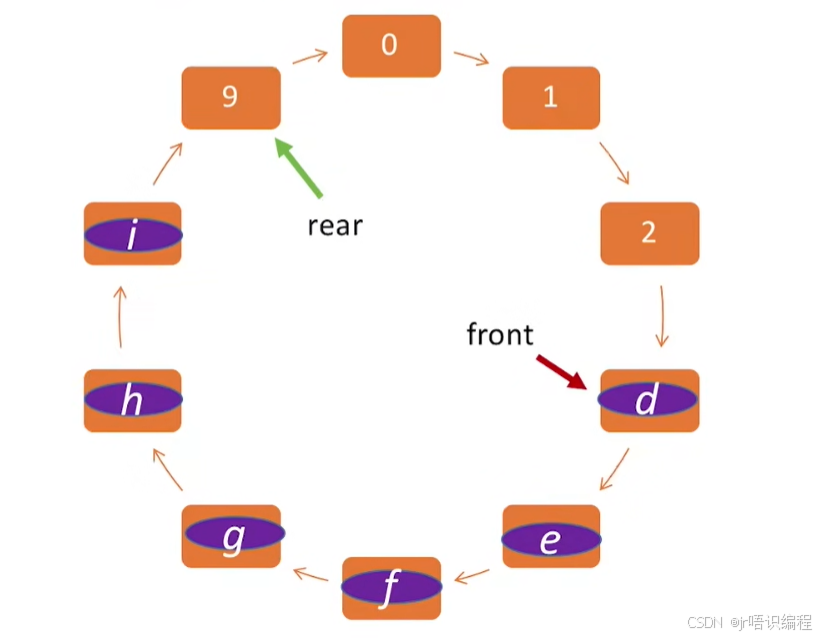
{0,1,2,…,MaxSize-1}将存储空间在逻辑上变成了“环状“
模运算将无限的整数域映射到有限的整数集合{0,1,2,…,b-1}上
循环队列:用模运算将存储空间在逻辑上变成了“环状“
队列已满的条件:队尾指针再下一个位置是对头,即(Q.rear+1)%MaxSize==Q.front
代价:牺牲一个存储单元
队满:if((Q.rear+1)%MaxSize==Q.front)
循环队列——出队操作:
//出队(删除一队头元素,并用x返回)
bool DeQueue(SqQueue &Q,ElemType &x){
if(Q.rear==Q.front)
return false; //队空则报错
x=Q.data[Q.front];
Q.front=(Q.front+1)%MaxSize;
return true;
}
//获得队头元素的值,用x返回
bool GetHead(SqQueue Q,ElemType &x)
if(Q.rear==Q.front)
x.Q.data[Q.front];
return true;
}队列元素个数:
(rear+MaxSize-front)%MaxSize
不浪费那一个存储空间:
#define MaxiSize 10 //定义队列中元素的最大个数
typedef struct{
ElemType data[MaxSize]; //用静态数组存放队列元素
int front,rear; //队头指针和队尾指针
int size; //队列当前长度
}SqQueue;插入成功size++;
删除成功size--;
初始化时
rear=front=0;
size=0;
队满条件:size==MaxSize
队空条件:size==0;
确定判空判满的方法:
- 牺牲一个存储单元
- 增加size变量记录队列长度
- 增加tag=0/1用于标记最近的一次操作是出队/入队
3.2.3_队列的链式实现
typedef struct LinkNode{ //链式队列结点
ElemType data;
struct LinkNode *next;
}LinkNode;
typedef struct{ //链式队列
LinkNode *front, *rear; //队列的队头和队尾指针
}LinkQueue;链队列——链式存储实现的队列
初始化(带头结点):
void InitQueue(LinkQueue &Q){
//初始化时front、rear都指向头结点
Q.front=Q.rear=(LinkNode*)malloc(sizeof(LinkNode));
Q.front->next=NULL;
}
void testLinkQueue(){
LinkQueue Q; //声明一个队列
InitQueue(Q); //初始化队列
//后续操作
}
//判断队列是否为空(不带头结点)
bool IsEmpty(LinkQueue Q){
if(Q.front==NULL)
return true;
else
return false;
}入队(带头结点):
//新元素入队(带头结点)
void EnQueue(LinkQueue &Q,ElemType x){
LinkNode *s=(LinkNode *)malloc(sizeof(MaxSize));
s->data=x;
s->next=NULL;
Q.rear->next=s; //新结点插入到rear之后
Q.rear=s; //修改表尾指针
}入队(不带头结点)
//新元素入队(不带头结点)
void EnQueue(LinkQueue &Q,ElemType x){
LinkNode *s=(LinkNode *)malloc(sizeof(MaxSize));
s->data=x;
s->next=NULL;
if(Q.front==NULL){ //在空列表中插入第一个元素
Q.front=s; //修改队头队尾指针
Q.rear=s; //不带头结点的队列,第一个元素入队时需要特别处理
}else{
Q.rear->next=s; //新结点插入到rear之后
Q.rear=s; //修改表尾指针
}
}出队(带头结点):
//队头元素出队(不带头结点)
bool DeQueue(LinkQueue &Q,ElemType &x){
if(Q.front==Q.rear)
return false; //空队
LinkNode *p=Q.front->next;
x=p->data //用变量x返回队头元素
Q.front->next=p->next; //修改头结点的next指针
if(Q.rear==p) //此次是最后一个结点出队
Q.rear=Q.front //修改rear指针
free(p); //释放结点空间
return true;
}顺式存储——预分配的空间耗尽时队满
链式存储——一般不会队满,除非内存不足
3.2.4_双端队列
双端队列:只允许从两端插入、两端删除的线性表
考察:判断输出序列合法性
若数据元素输入序列为1,2,3,4,则哪些输出序列是合法的,哪些是非法的
输入受限的双端队列:允许从两端删除、从一端插入的队列
输出受限的双端队列:允许从两端插入、从一端删除的队列
栈中合法的序列,双端队列中一定也合法
3.3.1_栈在括号匹配中的应用
最后出现的左括号最先被匹配(LIFO),可用“栈“实现该特性
每出现一个右括号,就“消耗”一个左括号(出栈)
遇到左括号就入栈
遇到右括号,就“消耗”一个左括号
bool backetCheck(char str[ ],int length){
SqStack S;
InitStack(S); //初始化一个栈
for(int i=0;i<length;i++){
if(str[i]==’(‘ || str[i]==’[‘ || str[i]==’{‘ ){
Push(S,str[i]); //扫描到左括号,入栈
} else{
if(StackEmpty(S)) //扫描到右括号,且当前栈空
return false; //匹配失败
char topElem;
Pop(S,topElem); //栈顶元素出栈
if(str[i]==’)’ && topElem!=’(‘)
return false;
if(str[i]==’]’ && topElem!=’[‘)
return false;
if(str[i]==’}’ && topElem!=’{‘)
return false;
}
}
return StackEmpty(S); //检索完全部括号后,栈空说明匹配成功
}#define MaxSize 10 //定义栈中元素的最大值
typedef struct{
char data[MaxSize]; //静态数组存放栈中元素
int top; //栈顶指针
} SqStack;//初始化栈
void InitStack(SqStack &S)
//判断栈是否为空
bool StackEmpty(SqStack S)
//新元素入栈
bool Push(SqStack &S,char x)
//栈顶元素出栈,用x返回
bool Pop(SqStack &S,char &x)用栈实现括号匹配:
依次扫描所有字符,遇到左括号入栈,遇到右括号,则弹出栈顶元素检查是否匹配。
匹配失败情况:
左括号单、右括号单、左右括号不匹配
3.3.2_栈在表达式求值中的应用(上)
中缀表达式:运算符在两个操作数中间
a+b
后缀表达式:运算符在两个操作数后面
ab+
前缀表达式:运算符在两个操作数前面
+ab
中缀转后缀的手算方式:
- 确定中缀表达式中各个运算符的运算顺序
- 选择下一个运算符,按照(左操作数 右操作数 运算符)的方式组合成一个新的操作数
- 如果还有运算符没被处理,就继续2
“左优先”原则:只要左边的运算符能先运算,就优先算左边的
后缀表达式的手算方法:
从左往右扫描,每遇到一个运算符,就让运算符前面最近的两个操作数执行对应运算,合体为一个操作数
用栈实现后缀表达式的计算:
- 从左往右扫描下一个元素,直到处理完所有元素
- 若扫描到操作数则压入栈,并回到1;否则执行3
- 若扫描到运算符,则弹出两个栈顶元素,执行相应运算,运算结果压回栈顶,回到1
注意:先出栈的是“右操作数”
若表达式合法,则最后栈中只会留下一个元素,就是最终结果
后缀表达式适用于基于栈的编程语言
中缀转前缀的手算方法:
- 确定中缀表达式中各个运算符的运算顺序
- 选择下一个运算符,按照(运算符 左操作数 右操作数)的方式组合成一个新的操作数
- 如果还有运算符没被处理,请继续2
“右优先”原则:只要右边的运算符能先计算,就优先算右边的
用栈实现前缀表达式的计算:
- 从右往左扫描下一个元素,直到处理完所有元素
- 若扫描到操作数则压入栈中,并回到1;否则执行3
- 若扫描到运算符,则弹出两个栈顶元素,执行相应运算,运算结果压回栈顶,回到1
注意:先出栈的是“左操作数”
3.3.2_栈在表达式求值中的应用(下)
中缀表达式转后缀表达式(计算)
初始化一个栈,用于保存暂时还不能确定运算顺序的运算符。
从左到右处理各个元素,直到末尾。可能遇到三种情况:
- 遇到操作数。直接加入后缀表达式。
- 遇到界限符。遇到“(”直接入栈;遇到“)”则依次弹出栈内运算符并加入后缀表达式,直到弹出“(”为止。注意:“(”不加入后缀表达式。
- 遇到运算符。依次弹出栈中优先级高于或等于当前运算符的所有运算符,并加入后缀表达式,若碰到“(”或栈空则停止。之后再把当前运算符入栈。
按上述方法处理完所有字符后,将栈中剩余运算符依次弹出,并加入后缀表达式。
中缀表达式的计算(用栈实现)
中缀转后缀+后缀表达式求值两个算法的结合
用栈实现中缀表达式的计算:
初始化两个栈,操作数栈和运算符栈
若扫描到操作数,压入操作数栈
若扫描到运算符或界限符,则按照“中缀转后缀”相同的逻辑压入运算符栈(期间也会弹出运算符,每当弹出一个运算符时,就需要弹出两个操作数栈的栈顶元素并执行相应运算,运算结果再压回操作数栈)
3.3.3_栈在递归中的应用
函数调用的特点:最后被调用的函数最先执行结束(LIFO)
函数调用时,需要用一个栈存储:
- 调用返回地址
- 实参
- 局部变量
栈在递归中的应用:
适合用“递归”算法解决:可以把原始问题转换为属性相同,但规模较小的问题
递归调用时,函数调用栈可称为“递归工作栈”
每进入一层递归,就将递归调用所需信息压入栈顶
每退出一层递归,就从栈顶弹出相应信息
缺点:太多层递归可能会导致栈溢出;可能包含很多重复计算
可以自定义栈将递归算法改造为非递归算法
3.3.4_队列的应用
多个进程争抢着使用有限的系统资源时,FCFS(先来先服务)是一种给常用策略
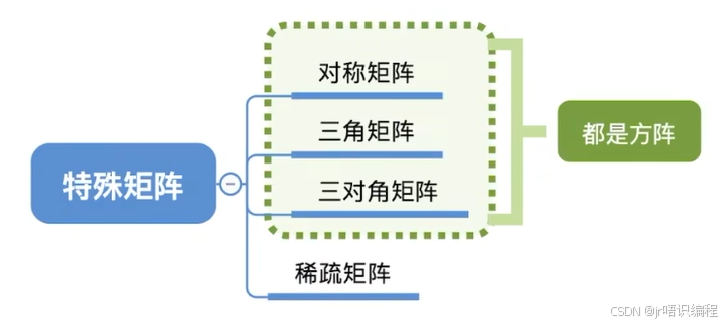
3.4_特殊矩阵的压缩存储
普通矩阵的存储
可用二维数组存储
注意:描述矩阵元素时,行、列号通常从1开始;而描述数组时通常下标从0开始
某些特殊矩阵可以压缩存储空间
对称矩阵的压缩存储
压缩存储策略:只存储主对角线+下三角区(或主对角线+上三角区)
按行优先原则将各元素存入一维数组中。
三角矩阵的压缩存储
下三角矩阵:除了主对角线和下三角区,其余的元素都相同
上三角矩阵:除了主对角线和上三角区,其余的元素都相同
压缩存储策略:按行优先原则将橙色区元素存储一维数组中。并在最后一个位置存储常量c
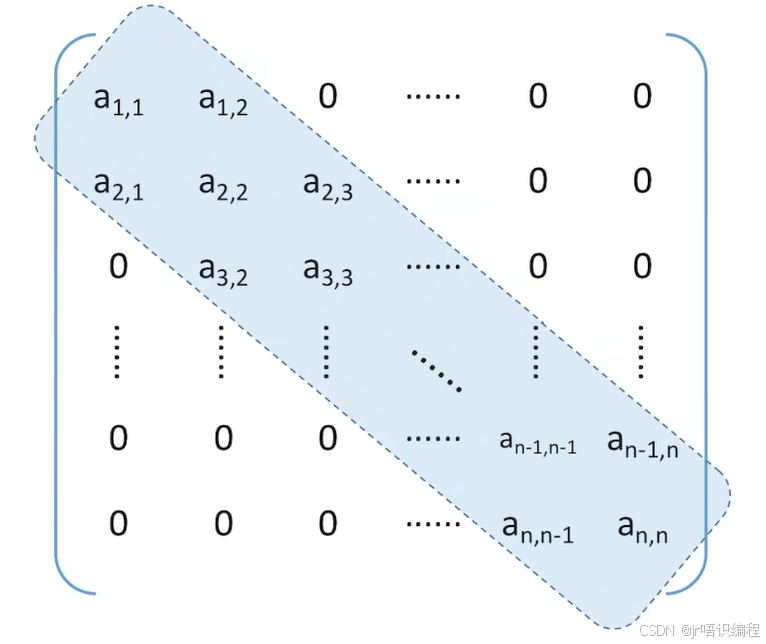
三对对角矩阵的压缩存储
三对角矩阵,又称带状矩阵:
当|i-j|>1时,元素为0
压缩存储策略:
按行优先(或列优先)原则,只存储带状部分
稀疏矩阵的压缩存储
稀疏矩阵:非零元素远远少于矩阵元素的个数
压缩存储策略:
顺序存储——三元组<行,列,值>
链式存储——十字链表法
易错点:
存储上三角?下三角?
行优先?列优先?
矩阵元素的下标从0?1?开始
数组下标从0?1?开始