一、什么是迭代学习
迭代学习是一种十分适合应用在重复性控制动作的控制方法,其大致原理是使用者通过对系统设计出一个学习率,并利用该学习率在系统的重复控制过程中一次一次迭代,以逐步减小系统误差,不断接近或达到系统的期望值。
迭代学习的关键主要在于:
- 逐步改进:每次迭代基于上一次迭代的结果进行优化。每次更新都会通过某种机制(如梯度下降)调整参数,以减少误差或损失函数。
- 反馈机制:模型的输出会提供反馈,指导下一步的学习和调整。反馈的形式通常是误差或损失度量。
- 广泛应用:迭代学习在许多机器学习和深度学习算法中都有应用,如线性回归、神经网络训练等,尤其是在优化问题中。
- 收敛过程:随着迭代次数的增加,模型的性能应该逐渐提升,直至收敛到某个最优解或达到设定的停止标准。
二、迭代学习具体方法和公式
下面我们逐步介绍迭代学习的公式。首先介绍什么是迭代学习率,然后介绍开环和闭环的迭代学习方式,并且一步步的如何改进迭代学习方法。
2.1 迭代学习率
迭代学习率是指每次模型参数更新时的步伐或变化量。它决定了模型在每一轮训练时,权重更新的速率。如果学习率太大,可能导致训练过程不稳定,权重更新过大,错过最优解;如果学习率太小,则可能导致收敛速度过慢,训练效率低下。 迭代学习可根据学习率的不同分为P型迭代学习、D型迭代学。
-
P型迭代学习
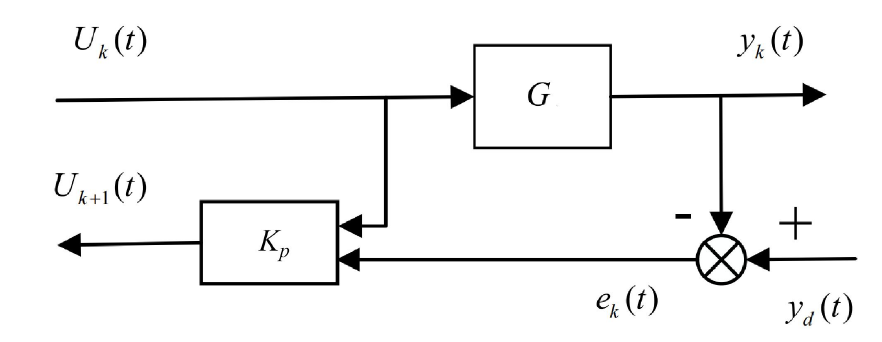
P型迭代学习就是带比例函数的迭代学习,最简单的P型迭代学习如下:
其中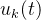
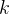
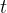

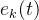
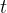
P型迭代学习的系统框图如下所示:
-
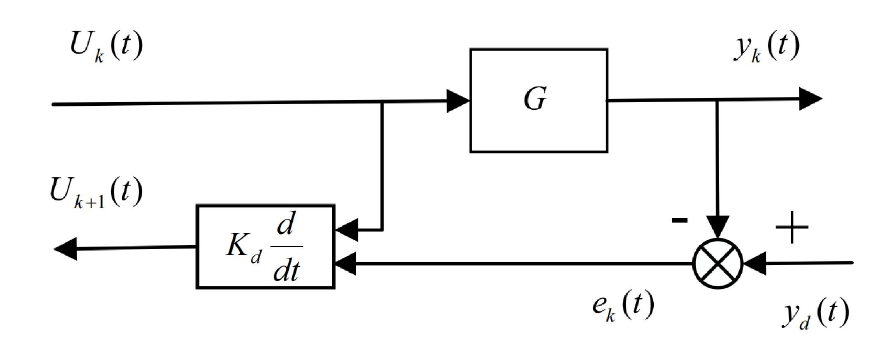
D型迭代学习
D型迭代学习用到的是跟踪误差的导数,最简单的D迭代学习公式如下:
其中
2.2 迭代反馈
控制系统基本都带有反馈,迭代学习作为控制系统的一种也需要反馈参与控制,而根据反馈方式的不同,可分为开环迭代学习和闭环迭代学习两种。
-
PD型开环迭代学习:
开环迭代学习是指第k+1次迭代的控制序列由第k次迭代产生的误差生成。用数学的方式可表示为:
其中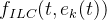

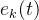
从另一个角度看,上述公式也可以看做是一个前馈控制, 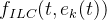
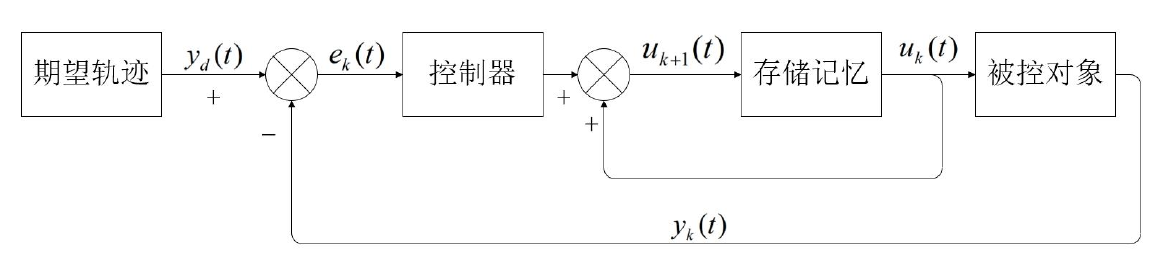
开环迭代学习系统框架图如下:
-
PD型闭环迭代学习
闭环迭代学习是指第k+1次迭代的控制序列由第k+1次迭代产生的误差生成。用数学的方式可表示为:
具体来说可以写做:
-
带低通滤波器的PD型闭环迭代学习:
为了除去信号中的高频噪声和未建模动态,可以加入低通滤波器。令低通滤波器为Q,则新的迭代学习控制率为:
-
带滤波器和遗忘因子的PD型开闭环高阶迭代学习
为了改善普通迭代学习的过度迭代问题,可以使用一种兼顾开环迭代学习和闭环迭代学习的高阶迭代学习方法。已知PD型开环迭代学习的控制率为:
我们知道开环迭代学习与闭环迭代学习的主要区别就是对误差的利用方式不同,闭环迭代学习中本次迭代产生的误差运用于本次的控制,属于实时补偿,开环迭代学习中本次迭代产生的误差运用于下一次迭代的控制,属于延时补偿,二者各有优缺点。闭环的收敛速度快,能立刻见效,但迭代过于激进,容易出现过度迭代,开环的收敛速度比闭环慢,但是不容易出现过度迭代。
如果将开环迭代学习与闭环迭代学习相结合,那么以PD型迭代学习为例,其迭代学习控制率为:
为了将每一次迭代所产生的的控制序列有效利用起来,又可将上面的式子改进为高阶迭代学习,以二阶为例:
其中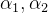
。
传统迭代学习在迭代的过程中不仅会产生过度迭代,而且如果无人为干预,其迭代的进程也不停止,会一直迭代下去。为了进一步弱化过度迭代带来的影响,并且锁定住迭代的过程中所产生的比较好的一次控制序列,引入遗忘因子对算法做约束:
其中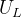
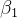

三、迭代学习的应用场景
3.1 梯度下降法(Gradient Descent)
-
应用场景:常用于监督学习中的模型训练,尤其是线性回归、逻辑回归、神经网络等。
-
原理:梯度下降是一种迭代优化方法,目标是通过不断更新模型的参数,最小化损失函数(如均方误差)。每次更新时,计算损失函数的梯度,并沿着梯度的反方向更新参数,直到损失函数收敛。
-
迭代学习过程:每次计算梯度并更新权重。重复此过程直到达到最优解或停止条件(如迭代次数、损失收敛)。
-
举例:训练神经网络时,通过梯度下降迭代更新每一层的权重,减少误差,优化模型性能。
3.2 神经网络训练
-
应用场景:深度学习中的神经网络训练(如卷积神经网络CNN、循环神经网络RNN等)。
-
原理:神经网络的训练通常使用反向传播算法(Backpropagation)和梯度下降法结合,通过迭代学习来调整网络权重。每次迭代中,神经网络会根据当前的预测输出与实际标签之间的误差来更新权重,从而优化网络性能。
-
迭代学习过程:首先输入训练数据,计算前向传播得到预测输出。然后计算损失函数(如交叉熵损失)并进行反向传播。最后更新参数,重复以上过程直到收敛。
-
举例:训练一个图像分类模型时,模型通过不断迭代调整权重,学习如何从图像中提取特征并进行准确分类。
3.3 支持向量机(SVM)
-
应用场景:分类问题,尤其是在高维数据或小样本学习中表现良好。
-
原理:支持向量机通过寻找最优超平面来将数据分成不同类别。在训练过程中,SVM通过迭代优化目标函数(最大化间隔和最小化分类误差)来更新支持向量的权重。
-
迭代学习过程:使用迭代的优化算法(如SMO,序列最小优化算法)来调整支持向量的位置和权重。并且每次迭代都在寻找最优的超平面,直到模型收敛。
-
举例:在情感分析中,通过训练SVM模型,根据输入文本的特征(如词频、TF-IDF等)进行分类,识别文本的情感倾向。
3.4 K-Means 聚类算法
-
应用场景:无监督学习中的聚类问题,常用于数据挖掘和模式识别。
-
原理:K-Means算法通过迭代过程将数据分成K个簇。每次迭代中,算法根据数据点的特征重新分配数据点到最近的簇中心,并计算新的簇中心,直到聚类结果稳定。
-
迭代学习过程:首先随机选择K个初始簇中心。然后将数据点分配给最近的簇中心。之后更新簇中心为该簇内所有数据点的均值。最后重复以上步骤直到簇中心不再变化(收敛)。
-
举例:在客户细分中,通过K-Means聚类分析客户的购买行为,将客户划分为不同的群体,帮助商家制定更精准的营销策略。
3.5 强化学习(Reinforcement Learning)
-
应用场景:智能体(agent)与环境进行交互,学习如何在动态环境中采取行动以最大化长期回报。
-
原理:强化学习通过迭代过程来优化策略。在每一步迭代中,智能体根据当前的状态选择一个动作,环境反馈奖励或惩罚,智能体根据奖励调整其策略,逐步优化其行为。
-
迭代学习过程:首先智能体与环境交互并根据当前策略做出决策,并收到环境的反馈(奖励或惩罚)。然后更新策略,以便在未来能获得更多的奖励。最后重复这个过程直到智能体学会最佳策略。
-
举例:在玩游戏时,强化学习通过不断调整决策策略,使得游戏中的智能体能够逐渐掌握如何赢得游戏。
3.6 遗传算法(Genetic Algorithm)
-
应用场景:优化问题,特别是当问题空间巨大且无法用传统优化方法求解时。
-
原理:遗传算法模拟自然选择的过程,通过迭代进化产生解。每一代中,算法根据适应度选择优秀的个体进行交叉、变异等操作,产生新的个体,直到找到最佳解。
-
迭代学习过程:首先初始化种群(随机生成一组候选解)。然后评估每个个体的适应度,适应度较高的个体进行交叉和变异,产生下一代个体。最后重复该过程,直到满足停止条件。
-
举例:在优化机器设计参数时,使用遗传算法通过迭代的方式,逐步找到最优的设计方案。