1. ROC曲线
ROC曲线,全称为“接收者操作特性(Receiver Operating Characteristic)”曲线,是一种反映灵敏度和特异度关系的图形工具。在机器学习和统计学中,ROC曲线常用于评估分类模型的性能。其主要特点是展示在不同分类阈值下模型的性能表现。通过调整不同的分类阈值,可以得到不同的假阳性率和真阳性率,这些点在ROC曲线中绘制出来,从而展现出模型的整体性能。AUC值(曲线下面积)则是衡量ROC曲线性能的量化指标。当模型的预测能力更好时,AUC值更高。另外,由于ROC曲线综合了准确率、召回率以及区分能力,它常用于不同分类算法之间的性能比较。
ROC 曲线用于展示在不同的分类阈值下,模型的真正类率(True Positive Rate, TPR)和假正类率(False Positive Rate, FPR)之间的关系。而AUC(Area Under the Curve)值则用以量化 ROC 曲线下的面积,是用于衡量分类器性能的一种指标。AUC值越接近1,表示分类器的性能越好。它考虑了分类器在不同阈值下的性能表现。
1.1 数学基础
- True Positive Rate(TPR)也称为灵敏度(Sensitivity)或召回率(Recall),是真正例(True Positive,TP)占所有实际正例(实际正例 = TP + FN)的比例。
- False Positive Rate(FPR)也称为1-特异性(1-Specificity),是假正例(False Positive,FP)占所有实际负例(实际负例 = FP + TN)的比例。
1.2 代码示例
ROC曲线仅适用于二分类问题,不是二分类问题应首先通过各种手段转为二分类问题。
- 简单二分类问题:
from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt
y_label = ([0, 0, 0, 1, 1, 1])
y_pre = ([0.3, 0.5, 0.9, 0.8, 0.4, 0.6])
fpr, tpr, thersholds = roc_curve(y_label, y_pre) # 非二进制需要pos_label用于确定正类
# sklearn.metrics.roc_curve(y_true, y_score, pos_label=None, sample_weight=None,
drop_intermediate=True)
for i, value in enumerate(thersholds):
print("%f %f %f" % (fpr[i], tpr[i], value))
roc_auc = auc(fpr, tpr)
# sklearn.metrics.roc_auc_score(y_true, y_score, average='macro', sample_weight=None)
plt.plot(fpr, tpr, 'k--', label='ROC (area = {0:.2f})'.format(roc_auc), lw=2)
plt.xlim([-0.05, 1.05]) # 设置x、y轴的上下限,以免和边缘重合,更好的观察图像的整体
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate') # 可以使用中文,但需要导入一些库即字体
plt.title('ROC Curve')
plt.legend(loc="lower right")
plt.show()- 多分类问题——以鸢尾花分类问题(三分类问题)为例:
from matplotlib import pyplot as plt
from sklearn import pipeline
from sklearn.datasets import load_iris
from sklearn.metrics import roc_curve, auc
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import label_binarize, StandardScaler
from sklearn.pipeline import Pipeline
# 导入数据集
iris = load_iris()
X = iris.data
y = iris.target
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0, test_size=0.3)
# 构建预处理和模型管道
pipeline = Pipeline([
('scaler', StandardScaler()), # 数据归一化
('knn', KNeighborsClassifier(n_neighbors=3)) # 选择模型
])
pipeline.fit(X_train, y_train)
y_pred = pipeline.predict(X_test)
# 由于ROC和AUC是二分类评估指标,需要对每个类别单独计算并绘制
Y_test_binarized = label_binarize(y_test, classes=[0, 1, 2])
n_classes = Y_test_binarized.shape[1]
fpr = dict()
tpr = dict()
roc_auc = dict()
# 计算每个类别的ROC曲线和AUC
for i in range(n_classes):
fpr[i], tpr[i], _ = roc_curve(Y_test_binarized[:, i], pipeline.predict_proba(X_test)[:, i])
roc_auc[i] = auc(fpr[i], tpr[i])
# 绘图
colors = ['aqua', 'darkorange', 'cornflowerblue']
plt.figure()
for i, color in zip(range(n_classes), colors):
plt.plot(fpr[i], tpr[i], color=color, lw=2, label=f'ROC curve of class {i} (area = {roc_auc[i]:0.2f})')
plt.plot([0, 1], [0, 1], 'k--', lw=2)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.legend(loc="lower right")
plt.show()参考链接:https://blog.csdn.net/ODIMAYA/article/details/103146608
2. PR曲线
PR曲线是精确率与召回率之间的关系曲线。通过调整分类阈值,可以得到不同的精确率和召回率组合,从而绘制出PR曲线。PR曲线下的面积(AP)也可以作为分类器性能的一个指标。
2.1 数学基础
2.2 代码示例
- 简单二分类问题:
from sklearn.metrics import precision_recall_curve, average_precision_score
import matplotlib.pyplot as plt
y_test = ([0, 0, 0, 1, 1, 1])
y_pred = ([0.3, 0.5, 0.9, 0.8, 0.4, 0.6])
precision, recall, thresholds = precision_recall_curve(y_test, y_pred)
# sklearn.metrics.precision_recall_curve(y_true, probas_pred, pos_label=None,
sample_weight=None)
# 计算AP
ap = average_precision_score(y_test, y_pred)
# sklearn.metrics.average_precision_score(y_true, y_score, *, average='macro', pos_label=1, sample_weight=None)
print(f"AP: {ap:.2f}")
# 绘制PR曲线
plt.plot(recall, precision, marker='.', label='PR (AP = {:.2f})'.format(ap))
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Precision-Recall Curve')
plt.legend()
plt.show()
- 多分类问题——以鸢尾花分类问题(三分类问题)为例:
from matplotlib import pyplot as plt
from sklearn.datasets import load_iris
from sklearn.metrics import auc, precision_recall_curve
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import label_binarize, StandardScaler
from sklearn.pipeline import Pipeline
# 导入数据集
iris = load_iris()
X = iris.data
y = iris.target
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0, test_size=0.3)
# 构建预处理和模型管道
pipeline = Pipeline([
('scaler', StandardScaler()), # 数据归一化
('knn', KNeighborsClassifier(n_neighbors=3)) # 选择模型
])
pipeline.fit(X_train, y_train)
y_pred = pipeline.predict(X_test)
Y_test_binarized = label_binarize(y_test, classes=[0, 1, 2])
n_classes = Y_test_binarized.shape[1]
precision = dict()
recall = dict()
average_precision = dict()
# 获取预测概率
y_scores = pipeline.predict_proba(X_test)
# 计算每个类的精度和召回率
for i in range(n_classes):
precision[i], recall[i], _ = precision_recall_curve(Y_test_binarized[:, i], y_scores[:, i])
average_precision[i] = auc(recall[i], precision[i]) # 计算平均精度
# 绘图
plt.figure(figsize=(7, 8))
colors = ['blue', 'orange', 'green'] # 为每个类定义特定颜色
for i in range(n_classes):
plt.plot(recall[i], precision[i], color=colors[i], lw=2,
label=f'class {i} (area = {average_precision[i]:0.2f})')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Precision-Recall Curve')
plt.legend(loc="lower left")
plt.show()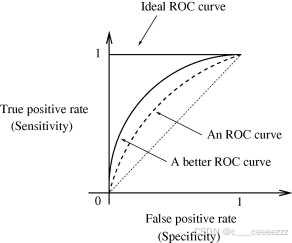
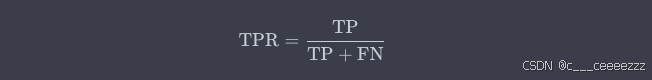


 https://blog.csdn.net/weixin_44012667/article/details/139988782?ops_request_misc=&request_id=&biz_id=102&utm_term=pr%E6%9B%B2%E7%BA%BF&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-0-139988782.142%5Ev100%5Epc_search_result_base5&spm=1018.2226.3001.4187
https://blog.csdn.net/weixin_44012667/article/details/139988782?ops_request_misc=&request_id=&biz_id=102&utm_term=pr%E6%9B%B2%E7%BA%BF&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-0-139988782.142%5Ev100%5Epc_search_result_base5&spm=1018.2226.3001.4187