章节概述

在本章中，我们总体研究树，特别提及连通图中的生成树以及 Cayley 在标记树计数方面的著名成果。

树的性质

基础定义

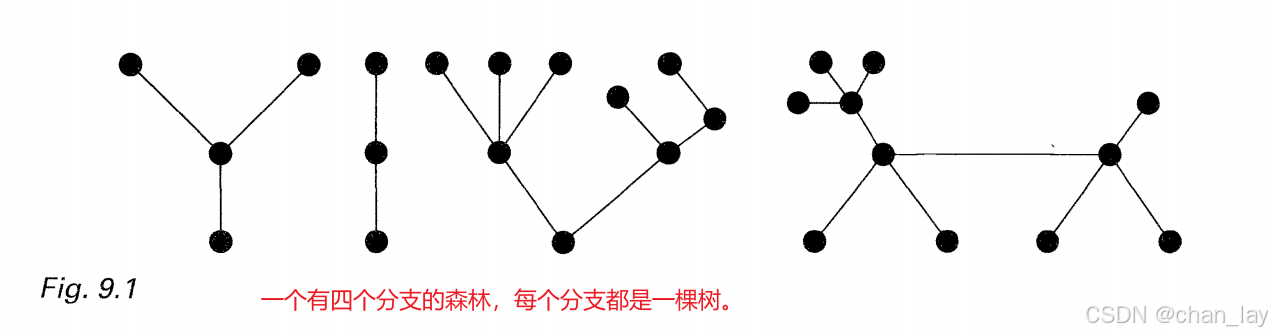
森林是不含圈的图，连通的森林就是树。注意，树和森林都是简单图。

基本性质

定理 9.1： 设 $T$ 是一个有 $n$ 个顶点的图。那么以下陈述是等价的：

• (i) $T$ 是一棵树；
• (ii) $T$ 不含圈， 且有 $n-1$ 条边
• (iii) $T$ 是连通的， 且有 $n-1$ 条边
• (iv) $T$ 是连通的， 且每条边都是一座桥
• (v) $T$ 的任意两个顶点恰好由一条路径连接
• (vi) $T$ 不含圈，但添加任何一条新边恰好产生一个圈

证明： 如果 $n=1$，上述六个结果显然成立；假设 $n\ge 2$

• （i）⇒（ii）
  • 数学归纳法：证明含有 $n$ 个顶点的树有 $n-1$ 条边
    • 当 $n=1$ 时，树中只有一个顶点没有边，边数 = 顶点数 - 1 = 1 - 1 = 0，成立
    • 假设对于所有顶点数小于 n 的树，边数 = 顶点数 - 1
    • 由于 $T$ 不含圈，移除任何一条边必然会使 $T$ 断开成两个图，且这两个图都是树。若断开的第一棵树有 $n_1(n_1<n)$ 个顶点，则边数为 $n_1-1$；若第二棵树有 $n_2$ 个顶点，则边数为 $n_2-1$。
    • 由于 $T$ 的顶点总数为 $n$，则 $n_1+n_2=n$；$T$ 的总边数 $=(n_1-1)+(n_2-1)+1=n_1+n_2-1=n-1$（加上断开的那条边），则 $T$ 的总边数为 $n-1$，成立。
• （ii）⇒（iii）
  • 反证法：证明 $T$ 是连通的
    • 如果 $T$ 是不连通的，那么 $T$ 的每个分支都是不含圈的连通图，也就是说 $T$ 的每个分支都是一棵树。
    • 设 $T$ 的每个分支为 $T_1,T_2,\cdots ,T_k(k\ge 2)$，根据上述定理，每个树中的顶点数比边数多 $1$，则对于 $T_i$，若其顶点数为 $n_i$，边数为 $m_i$，则 $n_i=m_i+1$。那么 $T$ 的总顶点数为 $n={\sum }_{i=1}^k{n}_i$，总边数为 $m={\sum }_{i=1}^k{m}_i$，则 $n=m+k$，$n-m=k\ge 2$。
    • 由此可知，$T$ 的顶点总数至少比边总数多 $2$，这与 $T$ 有 $n-1$ 条边这一事实相矛盾。
• （iii）⇒（iv）
  • 证明：$T$ 中每条边都是桥
    • 由于 $T$ 是连通的，且 $T$ 有 $n-1$ 条边，移除任何一条边后，图的顶点数仍为 $n$ ，但边数变为 $n-2$​​ 条。
    • 根据定理5.2，在一个图中，若边数 < 顶点数 - 1，该图必然是不连通的，意味着在 $T$ 中移除任意一条边都会使图的连通分量增加，说明 $T$ 中的每条边都是桥。
    • 定理5.2：设 $G$ 是一个具有 $n$ 个顶点的简单图。如果 $G$ 有 $k$ 个连通分量，那么 $G$ 的边数 $m$ 满足 $n-k\le m\le (n-k)(n-k+1)/2$。
• （iv）⇒（v）
  • 反证法：证明 $T$ 的任意两个顶点恰好只由一条路径连接。
    • 因为 $T$ 是连通的，所以每对顶点至少由一条路径连接。
    • 如果某一对顶点由两条路径连接，那么它们就围成了一个圈，如果存在圈，那么圈上的边就不是桥（因为移除圈上的边不会使图不连通）。这与每条边都是桥这一事实相矛盾。
• （v）⇒（vi）
  • 反证法：证明 $T$ 不含圈，但添加任何一条新边恰好产生一个圈
    • 如果 $T$ 包含一个圈，那么该圈中的任意两个顶点将至少由两条路径连接，这与陈述 $v$ 相矛盾。
    • 如果将一条边 $e=uv$ 添加到 $T$ 中，由于顶点 $u$ 和 $v$ 在 $T$​ 中已经是连通的，那么添加边 $e$ 后就会形成一个圈。
• （vi）⇒（i）
  • 证明：若 $T$ 不含圈，但添加任何一条新边恰好产生一个圈，则 $T$ 是一棵树。
    • 已知不含圈的连通图就是树，已知 $T$ 不含圈，只需再证明 $T$ 是连通的，就可以证明 $T$ 是一棵树。
    • 反证法：假设 $T$ 是不连通的。如果我们向 $T$ 添加任意一条连接其一个分支中的顶点与另一个分支中的顶点的边，那么不会形成圈。 与条件矛盾，说明 $T$ 是连通的。

推论9.2：如果 $G$ 是一个有 $n$ 个顶点且有 $k$ 个分支的森林，那么 $G$ 有 $n-k$ 条边。

证明：

• $G$ 的每个分支都是一棵树， 设这 $k$ 个树为 $T_1,T_2,\cdots ,T_k$，任意的 $T_i$ 都是连通的，若顶点数为 $n_i$ ，边数为 $m_i$，则有 $m_i=n_i-1$ 。
• $G$ 的总顶点数为 $n$，则 $n={\sum }_{i=1}^k{n}_i$；总边数为 $m={\sum }_{i=1}^k{m}_i={\sum }_{i=1}^k{n}_i-k=n-k$，则 $G$ 有 $n-k$ 条边。

注意，一棵树的 $n$ 个顶点的度数之和等于边数的两倍（$=2(n-1)=2n-2$）。由此可得，如果 $n>2$，那么任何具有 $n$​​​ 个顶点的树至少有两个端点（叶子节点）。

证明：

• 假设树只有一个端点（叶子节点），那么除该端点外的 $n-1$ 个顶点的度数至少为 $2$（因为非端点顶点至少与两条边相连），这样所有顶点度数之和至少为 $2(n-1)+1=2n-1$，这与由握手引理得出的 $2n-2$ 矛盾。
• 所以当 $n>2$ 时，树不可能只有一个端点，即任何具有 $n$ 个顶点的树至少有两个端点（叶子节点）。

生成树和生成森林

基本定义

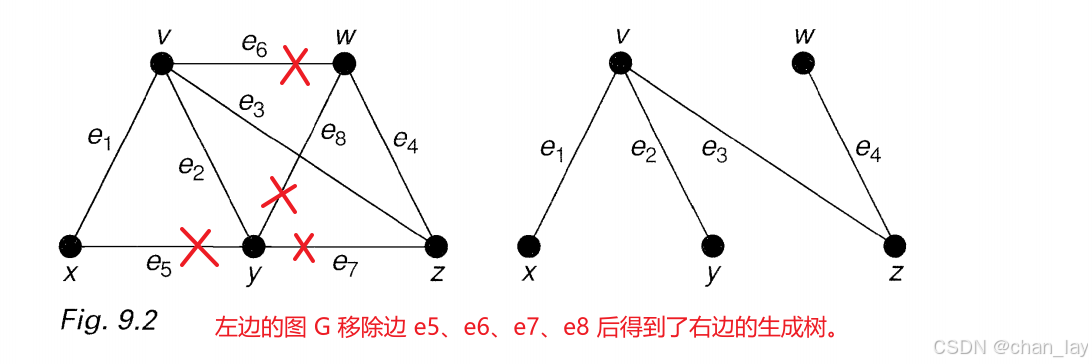
生成树：给定任意一个连通图 $G$，一棵连接 $G$ 所有顶点的树被称作 $G$​ 的生成树（spanning tree）。

1. 包含所有顶点：生成树包含原图中的所有顶点。
2. 树结构：生成树是一个树，这意味着它是连通的（任意两个顶点之间都有一条路径）且没有环（没有回路）。

生成森林： 生成森林是由若干棵生成树组成的，它包含了非连通图 $G$​ 中的所有顶点，但构成这些树的边是最少的。

给定一个连通图 $G$​，如何得到生成树：

对于任意一个连通图，我们可以选定一个圈，然后移除这个圈上的任意一条边，得到的图依然是连通的。我们对剩下的圈重复这一操作，持续进行下去，直到不再有圈为止。最终剩下的图就是生成树。

给定一个非连通图 $G$，如何得到生成森林：

如果 $G$ 是一个具有 $n$ 个顶点、$m$ 条边和 $k$ 个分支的任意图，那么对 $G$ 的每个分支树执行上述构建生成树的操作，所得的结果就是生成森林，在此过程中移除的边的总数就是 $G$ 的圈秩（cycle rank），用 $\gamma (G)$​​ 表示。

根据定理 5.2，$\gamma (G)=m-(n-k)=m-n+k$，它是一个非负整数。

为了方便，我们将 $G$ 的割集秩（cutset rank）定义为生成森林中的边数，用$\xi (G)$表示，根据推论 9.2，$\xi (G)=n-k$​。

• 回顾 推论9.2：如果 $G$ 是一个有 $n$ 个顶点且有 $k$ 个分支的森林，那么 $G$ 有 $n-k$​ 条边。

生成森林的性质

在本定理中，（不一定是简单图）图 $G$ 的生成森林 $T$ 的补图（complement）是通过从图 $G$ 中移除生成森林的边后所得到的图。

定理9.3：如果 $T$ 是图 $G$ 的任意一个生成森林，那么

• $G$ 的每个割集都与 $T$ 有一条公共边；
  • 证明：设 $C^{\ast }$ 为 $G$ 的一个割集，移除该割集会将 $G$ 的一个分支分割成两个子图 $H$ 和 $K$。
  • 由于 $T$ 是一个生成森林，它是包含了图 $G$ 中所有顶点的无圈连通子图。而原来顶点 $H$ 和 $K$ 是连通的，所以 $T$ 必定包含一条连接 $H$ 中一个顶点与 $K$ 中一个顶点的边，而这条边就是公共边。
• $G$ 的每个圈都与 $T$​ 的补图有一条公共边。
  • 反证法：假设 $C$ 是 $G$ 中的一个圈，它与 $T$ 的补图没有公共边。那么 $C$ 必定包含在 $T$ 中，这就产生了矛盾。

基本圈集和基本割集

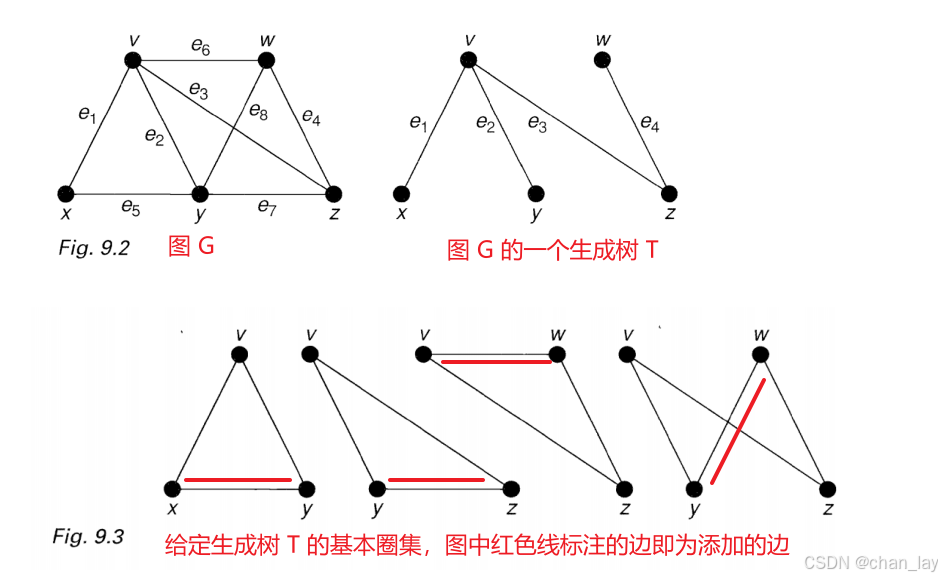
基本圈集(fundamental set of cycles)：

图 $G$ 的生成森林 $T$ 的基本圈集形成方式如下：如果我们向 $T$ 添加 $G$ 中任何一条不在 $T$ 中的边，我们会得到一个唯一的圈。通过分别添加 $G$ 中不在 $T$ 里的每一条边，以这种方式形成的所有圈的集合，就是与 $T$ 相关联的基本圈集。

请注意，任何基本圈集中圈的数量必定等于 $G$ 的圈秩。

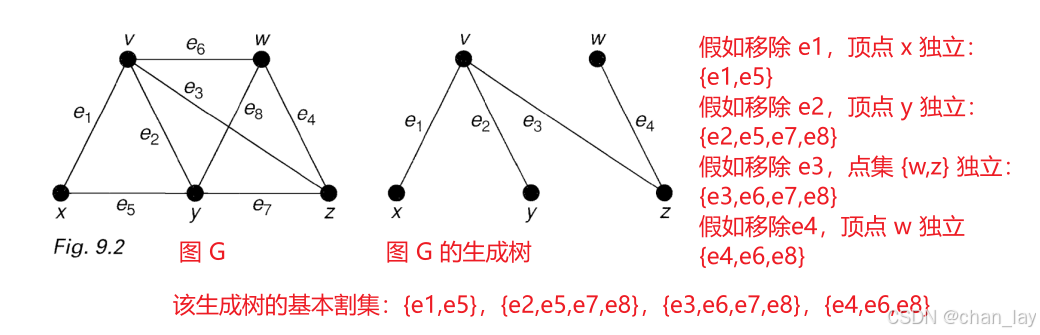
基本割集(fundamental set of cutsets)：

给定图 $G$ 的生成森林 $T$，依据定理 9.1（iv），树中的每一条边都是桥，意味着移除 $T$ 中的任意一条边会将 $T$ 的顶点集划分成两个不相交的集合 $V_1$ 和 $V_2$。图 $G$ 中所有连接 $V_1$ 中的一个顶点与 $V_2$ 中的一个顶点的边所构成的集合就是 $G$ 的一个割集，通过分别移除 $T$ 的每一条边得到的所有割集的集合就是与 $T$ 相关联的基本割集。

请注意，任何基本割集组中割集的数量必定等于 $G$​ 的割集秩。