有效括号序列
给出一个仅包含字符'(',')','{','}','['和']',的字符串,判断给出的字符串是否是合法的括号序列
括号必须以正确的顺序关闭,"()"和"()[]{}"都是合法的括号序列,但"(]"和"([)]"不合法。
题目思路 :
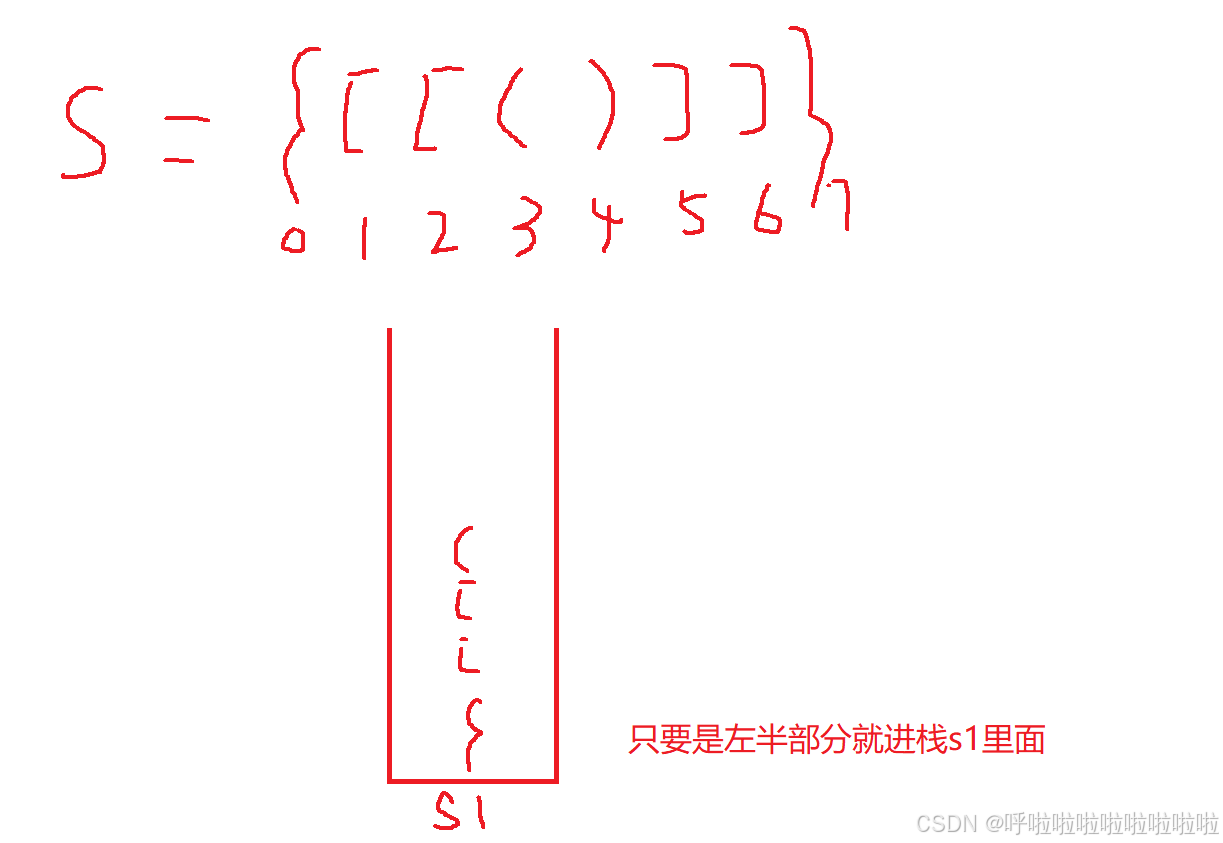
每次遇到'(','{','['这三种字符的时候,将字符入栈stk;而每次遇到')','}',']'这三种字符的时候则让对应的匹配字符出栈。
细节处理:当第一个字符为右边部分可以直接返回false 或只有一个字符
public boolean isValid (String s) {
int len = s.length();
//单数直接false 或者第一个字符为右半半部分
char ss = s.charAt(0);
if(len %2 == 1 || ss == ')' || ss == ']' || ss == '}' ) {
return false;
}
Stack<Character> s1 = new Stack<>();
for(int i = 0;i < len ; i++) {
char ch = s.charAt(i);
if(ch == '(' || ch == '[' || ch == '{') {
s1.push(ch);
} else {
//拿出栈顶元素
char ch1 = s1.peek();
if(ch == ')' && ch1 == '('
|| ch == ']' && ch1 == '['
|| ch == '}' && ch1 == '{') {
s1.pop();
} else {
return false;
}
}
}
return s1.isEmpty();
}滑动窗口的最大值
给定一个长度为 n 的数组 num 和滑动窗口的大小 size ,找出所有滑动窗口里数值的最大值。
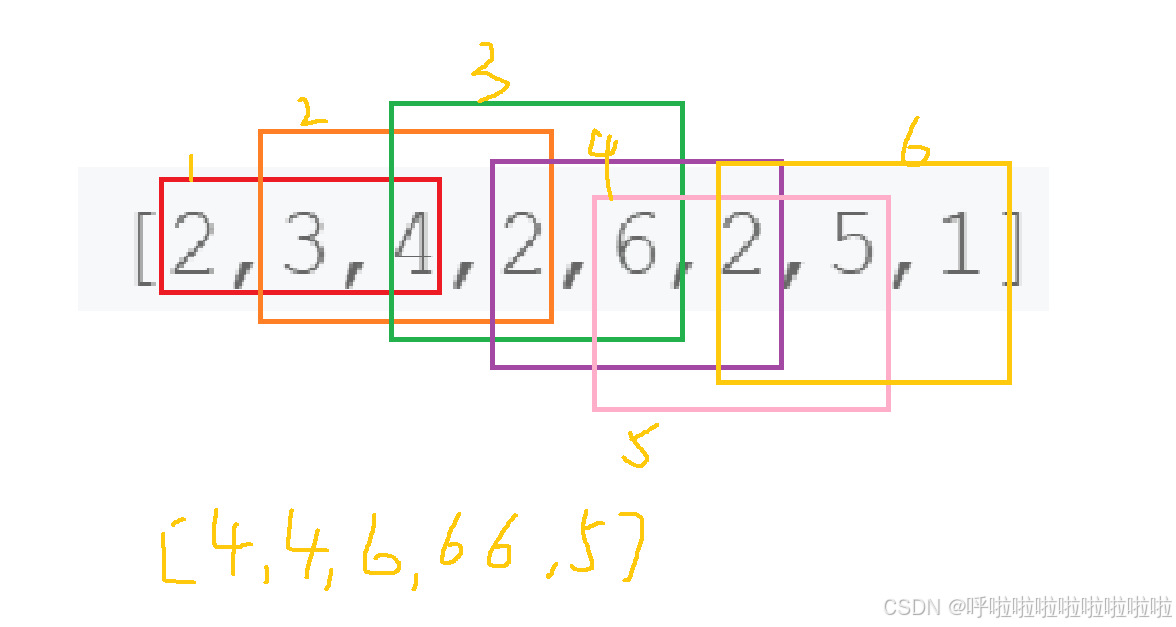
例如,如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3,那么一共存在6个滑动窗口,他们的最大值分别为{4,4,6,6,6,5}; 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个: {[2,3,4],2,6,2,5,1}, {2,[3,4,2],6,2,5,1}, {2,3,[4,2,6],2,5,1}, {2,3,4,[2,6,2],5,1}, {2,3,4,2,[6,2,5],1}, {2,3,4,2,6,[2,5,1]}。
窗口大于数组长度或窗口长度为0的时候,返回空。
题目分析
细节:当数组长度小于size 或者 size为0 直接返回空的
循环出口: 当right大于等于数组长度时候,即为完成
public ArrayList<Integer> maxInWindows (int[] num, int size) {
// write code here
ArrayList<Integer> ret = new ArrayList<>();
if(num.length < size || size == 0) {
return ret;
}
int left = 0 , right = size-1;
while(right < num.length) {
ret.add(getMax(num,left,right));
left++;
right++;
}
return ret;
}
public int getMax(int[] nums,int left,int right) {
int max = 0;
for(int i = left;i<=right;i++) {
if(max <= nums[i]) {
max = nums[i];
}
}
return max;
}最小的K个数
描述:
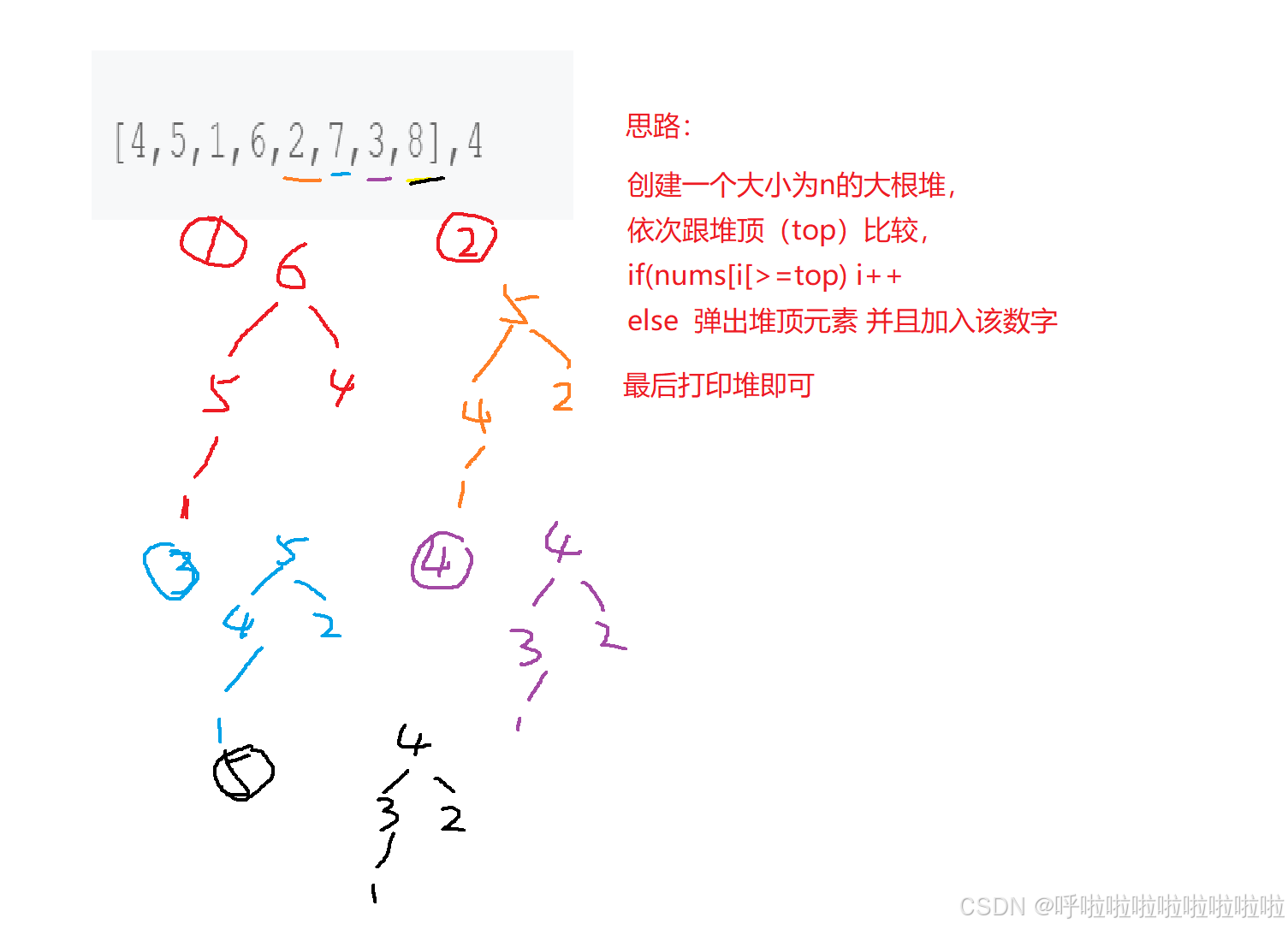
给定一个长度为 n 的可能有重复值的数组,找出其中不去重的最小的 k 个数。例如数组元素是4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4(任意顺序皆可)。
数据范围:0≤k,n≤100000≤k,n≤10000,数组中每个数的大小0≤val≤10000≤val≤1000
要求:空间复杂度 O(n)O(n) ,时间复杂度 O(nlogk)O(nlogk)
题目分析:
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param input int整型一维数组
* @param k int整型
* @return int整型ArrayList
*/
public ArrayList<Integer> GetLeastNumbers_Solution (int[] input, int k) {
// write code here
ArrayList<Integer> ret = new ArrayList<>();
if(k==0) {
return ret;
}
PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a,b)->{return b-a;});
//创建大小为k的大根堆
int i = 0;
for( i = 0;i<k;i++) {
maxHeap.offer(input[i]);
}
for(i = k;i<input.length;i++) {
int peek = maxHeap.peek();
if(peek >= input[i]) {
maxHeap.poll();
maxHeap.offer(input[i]);
}
}
return new ArrayList<>(maxHeap);
}
}寻找第k大
描述
有一个整数数组,请你根据快速排序的思路,找出数组中第 k 大的数。
给定一个整数数组 a ,同时给定它的大小n和要找的 k ,请返回第 k 大的数(包括重复的元素,不用去重),保证答案存在。
思路一
与上题目同理,使用堆
这次使用小跟堆即可
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param a int整型一维数组
* @param n int整型
* @param K int整型
* @return int整型
*/
public int findKth (int[] nums, int n, int k) {
// write code here
PriorityQueue<Integer> minHeap = new PriorityQueue<>((a, b)->a - b);
int i;
//使用一个含有 k 个元素的最小堆
for (i = 0; i < k; i++) {
minHeap.offer(nums[i]);
}
for (i = k; i < nums.length; i++) {
//看一眼,不拿出,因为有可能没有必要替换
int top = minHeap.peek();
if (top < nums[i]) {
minHeap.poll();
minHeap.offer(nums[i]);
}
}
return minHeap.poll();
}
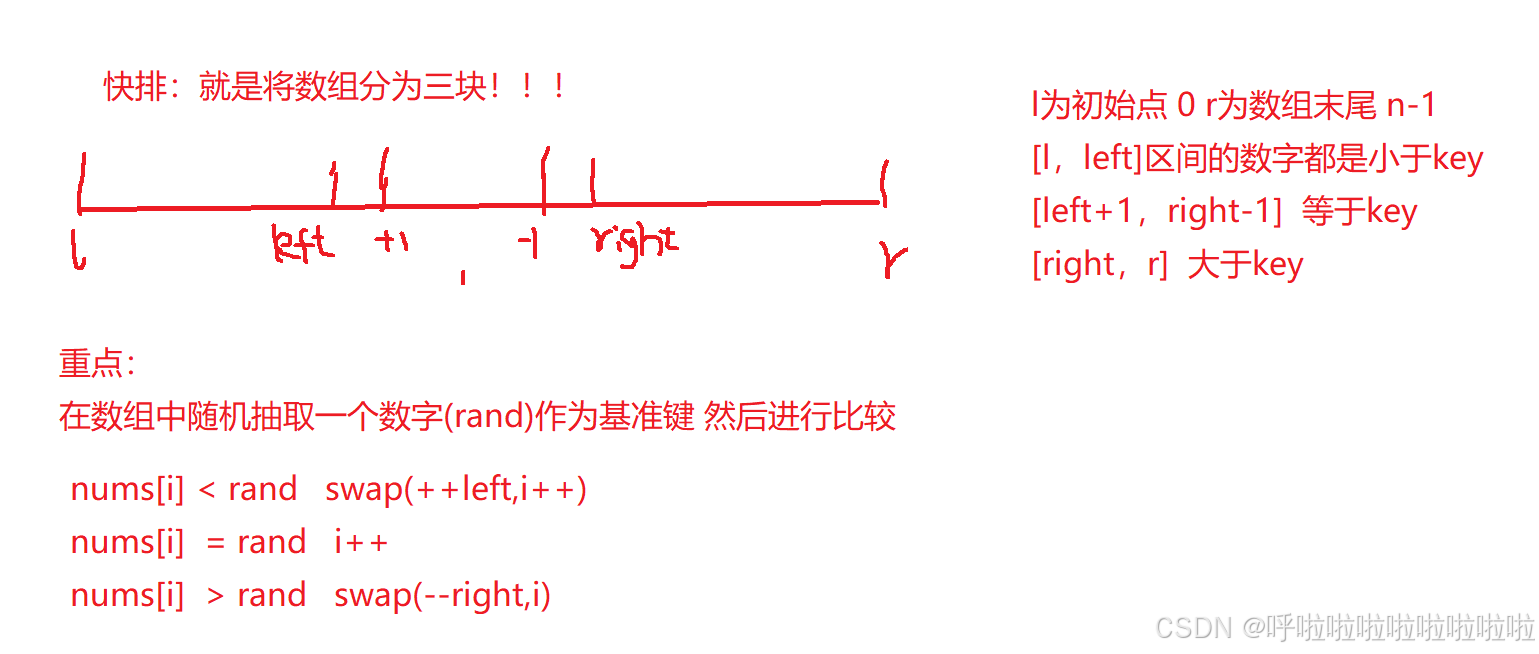
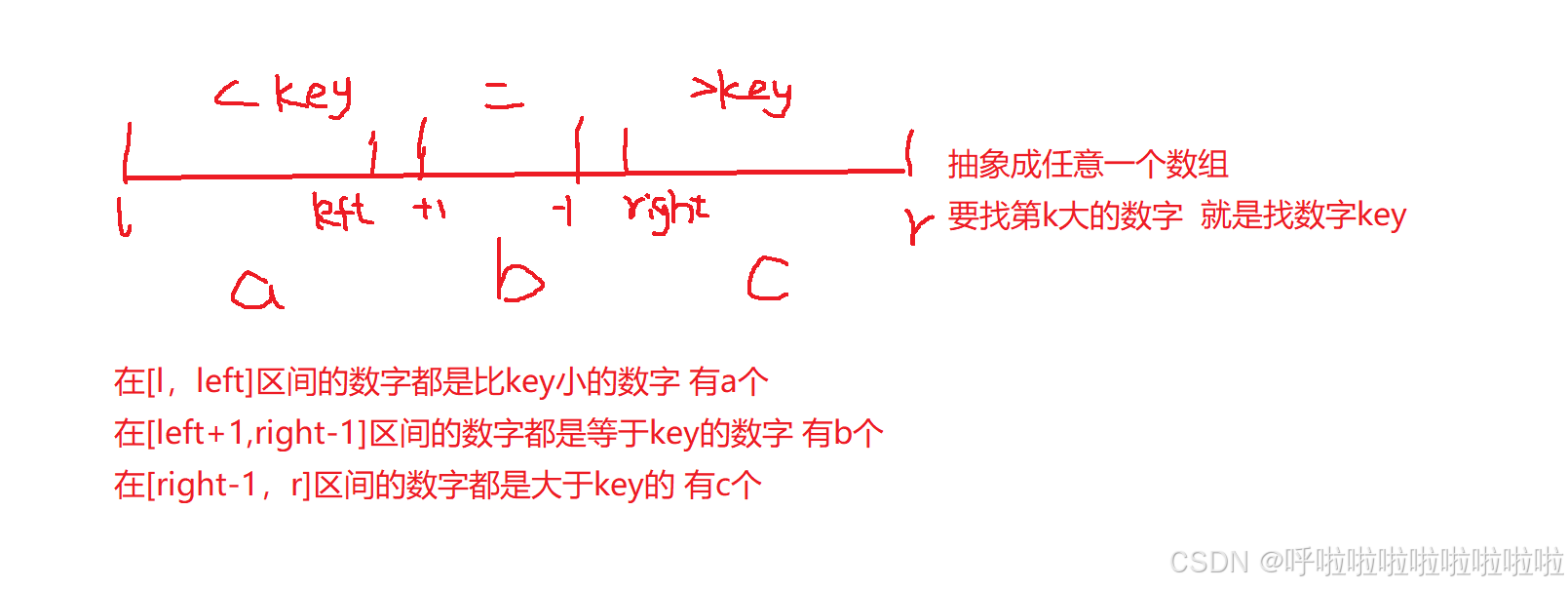
}思路二(快排思想):
随机数
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param a int整型一维数组
* @param n int整型
* @param K int整型
* @return int整型
*/
public int findKth (int[] a, int n, int K) {
// write code here
return qsort(a,0,n-1,K);
}
public int qsort(int[] nums,int l,int r,int k) {
//生成随机数
int key = nums[(l+r)/2];
int left = l-1 , right = r+1,i = l;
//划分区域
while(i < right) {
if(nums[i] < key) {
swap(nums,++left,i++);
} else if(nums[i] == key) {
i++;
} else {
swap(nums,--right,i);
}
}
//区间成型
//[l,left],[left+1,right-1],[right,r]
int c = r-right+1 , b = right -left -1 ;
if(c >= k) {
return qsort(nums,right,r,k);
} else if (b+c >= k) {
return key;
}else{
return qsort(nums,l,left,k-c-b);
}
}
public void swap(int[]nums,int l ,int r) {
int tmp = nums[l];
nums[l] = nums[r];
nums[r] = tmp;
}
}结语: 写博客不仅仅是为了分享学习经历,同时这也有利于我巩固知识点,总结该知识点,由于作者水平有限,对文章有任何问题的还请指出,接受大家的批评,让我改进。同时也希望读者们不吝啬你们的点赞+收藏+关注,你们的鼓励是我创作的最大动力!