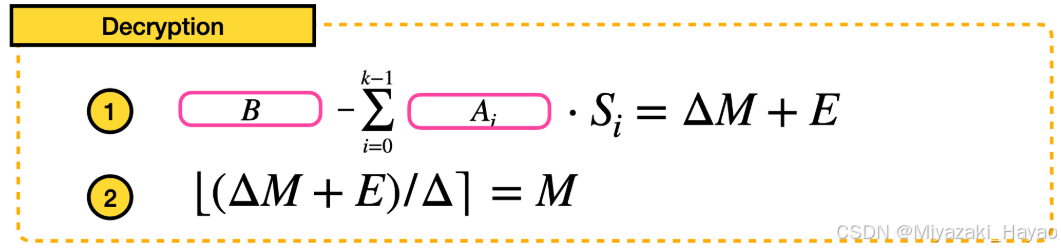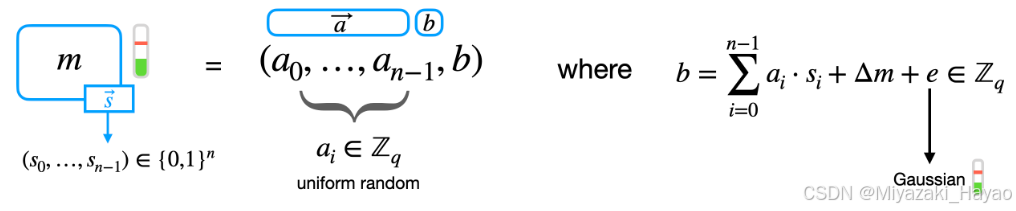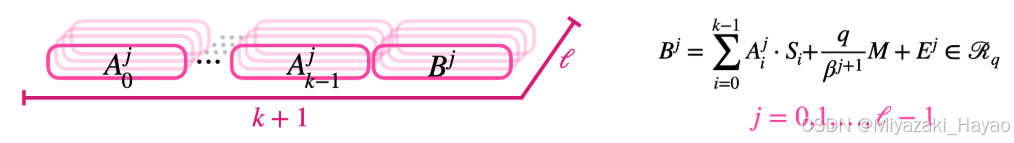文章目录
1. Abstract
TFHE 指的是 全同态加密策略。意思是,允许对密文进行运算,等价于对明文进行运算。TFHE 最初是作为 FHEW 方案的改进而提出的,然后开始向更广泛的方向发展。
该方案的 安全性 基于一个称为 带错误学习 (LWE) 的 困难格问题,及其变体,如 Ring LWE (RLWE)。事实上,目前使用的大多数 FHE 方案 都是 基于LWE 的,并且 使用有噪声的 密文。
然而,TFHE 与其他方法的区别在于,它提出了一种 特殊的自举 (bootstrapping),这种自举 速度非常快,能够在 降低噪声的同时评估函数。
在我们详细讨论 bootstrapping 之前,有必要写几篇博文,所以现在不要急于理解它是如何工作的。让我们从头开始描述 TFHE 中使用的 密文。
1.1 Some Conceptions
- R = Z [ X ] / ( X N + 1 ) R = Z[X] / (X^N + 1) R=Z[X]/(XN+1):表示 整数多项式环 (ring of integer polynomials) 模 圆分多项式 (cyclotomic polynomial) X N + 1 X^N+1 XN+1,N 是 2 的幂。实际上,它包含 一个 N-1 阶的整数多项式。
- R q = ( Z / q Z ) [ X ] / ( X N + 1 ) R_q = (Z / qZ) [X] / (X^N + 1) Rq=(Z/qZ)[X]/(XN+1):和上面相同的 整数环 R,但是这次 系数 是模 q。注意,我们通常将 Z / q Z Z / qZ Z/qZ 记为 Z q Z_q Zq。
- 我们的 模数约简 以 零 为中心。例如,当对 8 进行 模数约简 时,我们使用 同余类 { − 4 , − 3 , − 2 , − 1 , 0 , 1 , 2 , 3 } \{-4,-3,-2,-1,0,1,2,3\} {−4,−3,−2,−1,0,1,2,3},即 [ − q / 2 , q / 2 ) [-q/2,q/2) [−q/2,q/2)。
- χ μ , σ \chi_{\mu,\sigma} χμ,σ:是一个 均值 (mean) 为 μ \mu μ 标准差为 σ \sigma σ 高斯概率分布。如果 μ = 0 \mu = 0 μ=0,则简记为 χ σ \chi_\sigma χσ。
- 用 小写字母 表示 整数 (模) (a, b, m, s, …),使用 大写字母 表示 多项式 (A, B, M, S, …)。
- MSB 表示 最高有效位,LSB 表示 最低有效位。
- ⌊ ⌉ \lfloor\rceil ⌊⌉:表示舍入取整到最近的整数。
2. TFHE Ciphertexts
在 TFHE 中,我们主要使用三种类型的密文:LWE、RLWE、RGSW 密文。
为什么需要分为三类密文,原因是它们都 具有不同的属性,这些属性将在我们将在以下博客文章中描述的同态运算中有用。它们都具有 依赖于 LWE 问题或其变体的安全性。要了解有关 LWE 安全性的更多信息,请查看此 博客文章。
这些密文不仅用于 TFHE,也用于其他基于 LWE 的 FHE 方案。
- GLWE (General LWE) - LWE 和 RLWE 密文的概括
- GGSW (General GSW) - RGSW 密文的概括
- GLev - 一种 中间密文类型,对于更好地理解 GGSW 密文非常有用,并且我们将在后续的博客文章中大量使用它
3. GLWE
在本节中,我们将使用包含 LWE 和 RLWE 密文的概括,称为 General LWE,或简称 GLWE。
要生成任何类型的密文,我们首先需要一个 密钥。对于 GLWE 密文,密钥 是 R 中 k 个随机多项式 的列表 (每个 Si 都是一个 随机多项式):
S
→
=
(
S
0
,
.
.
.
,
S
k
−
1
)
∈
R
k
\overrightarrow{S} = (S_0,...,S_{k-1}) \in R^k
S=(S0,...,Sk−1)∈Rk 具体地,R 元素的系数可以从均匀二元分布、均匀三元分布、高斯分布或均匀分布中采样。
在本系列博客文章中,与原始 TFHE 描述一样,我们将假设我们的 密钥 是从 均匀二进制分布 中采样的。
现在看看如何 加密消息。令 q 和 p 为两个正整数,且 p <= q,并定义
Δ
=
q
/
p
\Delta = q/p
Δ=q/p。在 TFHE 中,q 和 p 通常被选为 2 的幂:如果不是,则应在 消息编码时 进行 四舍五入。
我们将 q 称为 密文模数,p 称为 明文模数,
Δ
\Delta
Δ 称为 缩放因子。让我们考虑一条 消息
M
∈
R
M \in R
M∈R。使用 密钥
S
→
\overrightarrow{S}
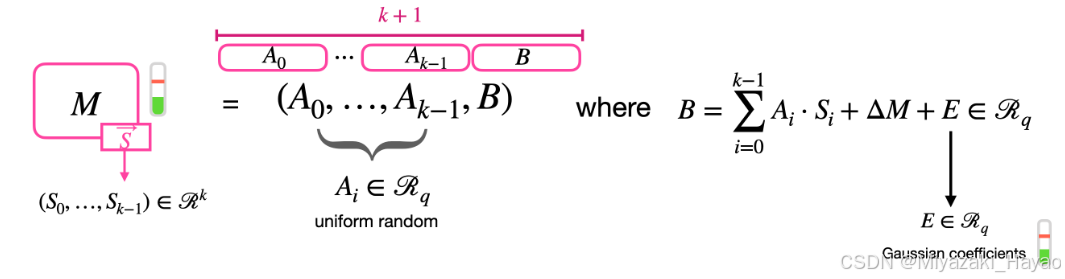
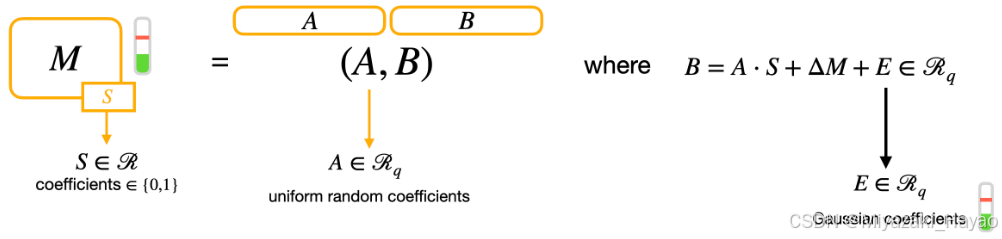
S 加密 消息 M 的 GLWE 密文 是一个 元组 (tuple):
(
A
0
,
.
.
.
,
A
k
−
1
,
B
)
∈
G
L
W
E
S
→
,
σ
(
Δ
M
)
⊆
R
q
k
+
1
(A_0,...,A_{k-1},B) \in GLWE_{\overrightarrow{S},\sigma}(\Delta M)\subseteq R_{q}^{k+1}
(A0,...,Ak−1,B)∈GLWES,σ(ΔM)⊆Rqk+1其中,Ai 是从 Rq 中 均匀随机抽样 出来的 (Ai 是一个 N次 多项式,系数 模 q,这个在第一部分 “一些概念” 中有提到)。并且
B
=
∑
i
=
0
k
−
1
A
i
∗
S
i
+
Δ
M
+
E
∈
R
q
B = \sum_{i=0}^{k-1}{A_i * S_i} + \Delta M + E \in R_q
B=∑i=0k−1Ai∗Si+ΔM+E∈Rq,且
E
∈
R
q
E \in R_q
E∈Rq 的参数是从 高斯分布
χ
σ
\chi_{\sigma}
χσ 中采样出来的。
多项式乘法 Ai * Si 记得模 (Xn+1)。
上面 Δ \Delta Δ 和 E 都是数,等价于 常数多项式
M 被编码到一个 多项式中
E 就是 噪声,即 noise error
我们通常称
(
A
0
,
.
.
.
,
A
k
−
1
)
(A_0,...,A_{k-1})
(A0,...,Ak−1) 为 mask,称 B 为 body。多项式
Δ
M
\Delta M
ΔM 就是常说的 M 的编码。
注意,为了计算
Δ
M
\Delta M
ΔM,我们 将 消息 M 编码到 Rq 中 (作为多项式)。而且,每次我们加密一条消息,都采用 新的随机性 (mask 和 noise error)。
在 密钥 S 下,具有 标准差 为
σ
\sigma
σ 的 高斯噪声 的 相同编码
Δ
M
\Delta M
ΔM 的 GLWE 加密集,将被记为
G
L
W
E
S
→
,
σ
(
Δ
M
)
GLWE_{\overrightarrow{S},\sigma}(\Delta M)
GLWES,σ(ΔM)
现在,如果我们有一个 密文
(
A
0
,
.
.
.
,
A
k
−
1
,
B
)
∈
G
L
W
E
S
→
,
σ
(
Δ
M
)
⊆
R
q
k
+
1
(A_0,...,A_{k-1},B) \in GLWE_{\overrightarrow{S},\sigma}(\Delta M)\subseteq R_{q}^{k+1}
(A0,...,Ak−1,B)∈GLWES,σ(ΔM)⊆Rqk+1,密钥为
S
→
=
(
S
0
,
S
1
,
.
.
.
,
S
k
−
1
)
∈
R
k
\overrightarrow{S} = (S_0,S_1,...,S_{k-1}) \in R^k
S=(S0,S1,...,Sk−1)∈Rk,然后我们便可以进行 解密:
- B − ∑ i = 0 k − 1 A i ∗ S i = Δ M + E ∈ R q B - \sum_{i=0}^{k-1} A_i * S_i = \Delta M + E \in R_q B−∑i=0k−1Ai∗Si=ΔM+E∈Rq
-
M
=
⌊
(
Δ
M
+
E
)
/
Δ
⌉
M = \lfloor (\Delta M + E)/\Delta \rceil
M=⌊(ΔM+E)/Δ⌉
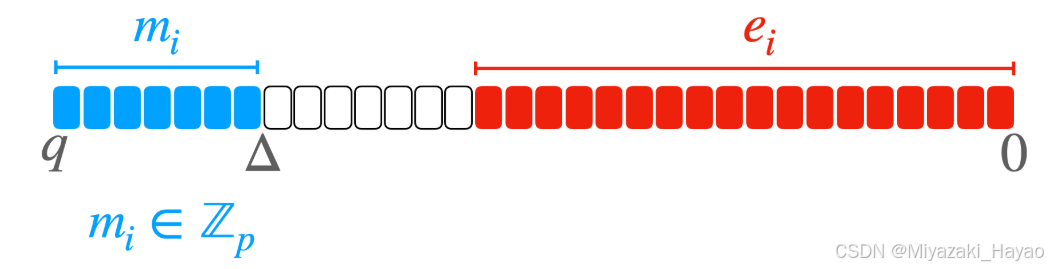
观察到 消息 M 位于 Δ M + E \Delta M+E ΔM+E 的 MSB 部分 (由于乘以 Δ \Delta Δ),而 E 位于 LSB 部分。
如果 ∣ E ∣ < Δ / 2 |E| < \Delta / 2 ∣E∣<Δ/2 (如果 E 的每个系数 ei 都有 ∣ e i ∣ < Δ / 2 |e_i| < \Delta / 2 ∣ei∣<Δ/2),则解密的第二部如期返回 M。如果 error 不符合条件,则解密不正确。在下图中,我们表示 Δ M + E \Delta M + E ΔM+E 的第 i 个系数。
可以看示例:博文中的 Toy example 部分
3.1 Trivial GLWE ciphertexts
在下一篇博文中,我们有时会使用所谓的 Trivial GLWE ciphertexts。这些密文不是真正的加密,因为它们隐藏了信息,但必须更多地将其视为 占位符:它们实际上 具有 GLWE 密文的形状,但 消息是明文。一个 Trivial GLWE ciphertexts 将所有的 Ai 设为 0,B 设为
Δ
M
\Delta M
ΔM。
(
0
,
0
,
.
.
.
,
0
,
Δ
M
)
∈
R
q
k
+
1
(0,0,...,0,\Delta M) \in R_{q}^{k+1}
(0,0,...,0,ΔM)∈Rqk+1 这些密文不是用来加密敏感信息的!在下一篇文章中,将展示如何使用它们在 同态计算 中注入 公开已知的数据。
3.2 LWE 和 RLWE
现在讨论如何从 GLWE 密文 中获取 LWE 密文 和 RLWE 密文。
当使用
k
=
n
∈
Z
和
N
=
1
k = n \in Z 和 N = 1
k=n∈Z和N=1 (k 表示密钥 S 包括 k 个 N 阶多项式,N 表示 多项式的次数) 实例化 GLWE 时,我们将获得 LWE。可以观察到,当 N = 1 时,Rq 就是 Zq。
当使用
k
=
1
和
N
=
2
r
k = 1 和 N = 2^r
k=1和N=2r 实例化 GLWE 时,我们获得 RLWE。
3.3 Public key encryption
上面使用私钥进行加密的,也可以使用公钥进行加密,详细内容在 该论文 中。
4. GLev
Glev 的主要作用是,识别 GLWE 和 GGSW 密文 之间的 中间密文类型,同时使 GGSW 密文 更易于理解。GLev 可以看作是 BGV 中使用的众所周知的 2 的幂加密 的泛化。
一个 Glev 密文包含 冗余:它由一组使用 不同的、非常精密的 缩放因子 Δ \Delta Δ 加密 相同消息 M 的 GLWE 密文 组成。 Δ \Delta Δ 由两个非常重要的参数来定义:
- 基数 β,通常是 2 的幂
- 级数 ℓ
( G L W E S → , σ ( q β 1 M ) × . . . × G L W E S → , σ ( q β ℓ M ) ) = G l e v S → , σ β , ℓ ( M ) ⊆ R q ℓ ⋅ ( k + 1 ) (GLWE_{\overrightarrow{S}, \sigma}(\frac{q}{\beta ^ 1} M) \times ... \times GLWE_{\overrightarrow{S}, \sigma}(\frac{q}{\beta ^ \ell} M)) = Glev_{\overrightarrow{S},\sigma}^{\beta,\ell}(M) \subseteq R_{q}^{\ell \cdot (k+1)} (GLWES,σ(β1qM)×...×GLWES,σ(βℓqM))=GlevS,σβ,ℓ(M)⊆Rqℓ⋅(k+1)如果 β 和 q 不是 2 的幂,在编码的时候就应该使用一个 rounding (取整操作)。
密钥与 GLWE 密文 的密钥一样。
解密的时候,只需使用相应的 缩放因子
Δ
\Delta
Δ 解密 其中一个 GLWE 密文 即可。因为 一个 Glev 密文 中包含的 一系列 GLWE 加密的都是 同一个消息 M。
4.1 Lev and RLev
正如我们看到 GLWE 是 LWE 和 RLWE 的 概括 一样,我们可以观察到,按照相同的规则,GLev 可以专门化为 Lev 和 RLev。
5. GGSW
知道了 GLWE 和 GLev 密文是什么,GGSW 就很好理解了:
- 一个 GLWE 密文是一个来自 Rq (或 一维举证) 的 元素向量
- 一个 Glev 密文是一个 元素为 GLWE密文 的向量 (或元素来自 Rq 的二维矩阵)
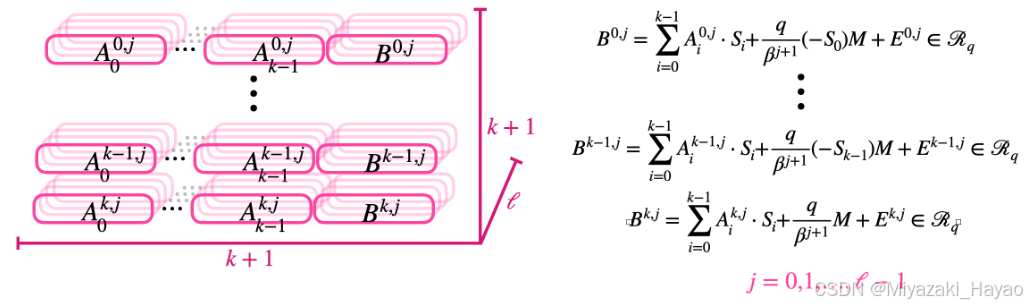
- 一个 GGSW 密文 是一个 元素为 Glev密文 的向量 (或元素来自 Rq 的三维矩阵,或 元素为 GLWE密文 的二维矩阵)
利用 GGSW 密文,我们再次 利用结构中的第三维 添加一些 冗余。具体来说,在 GGSW 中,每个 GLev 密文都会 加密 M 和 私钥中的一个多项式 Si 之间的 乘积:
密钥 与 GLWE 和 Glev 一样。
解密的时候,只需要解密 最后一个 Glev 密文 即可。
5.1 GSW and RGSW
正如在 GLWE 和 GLev 中看到的一样,我们可以观察到,GGSW 可以通过遵循之前提出的相同规则专门化为 GSW 和 RGSW。