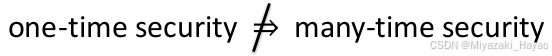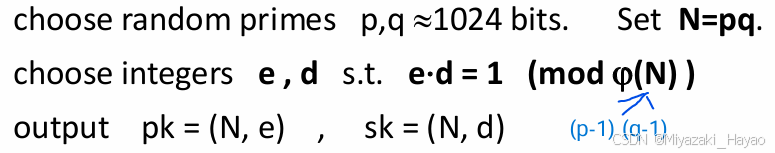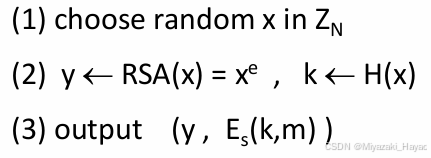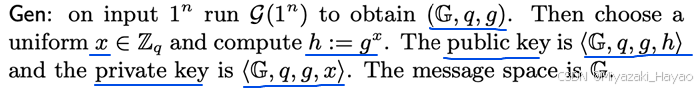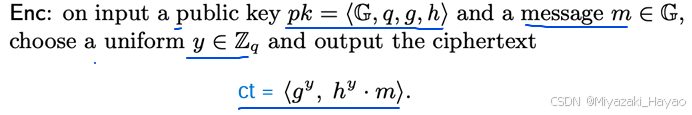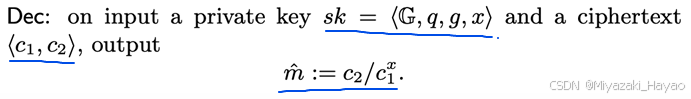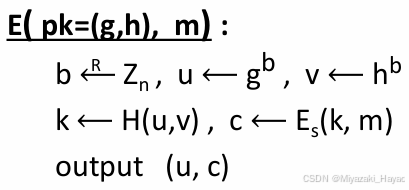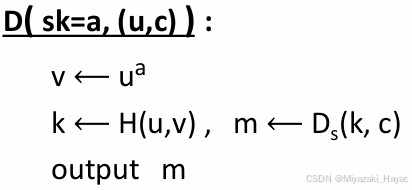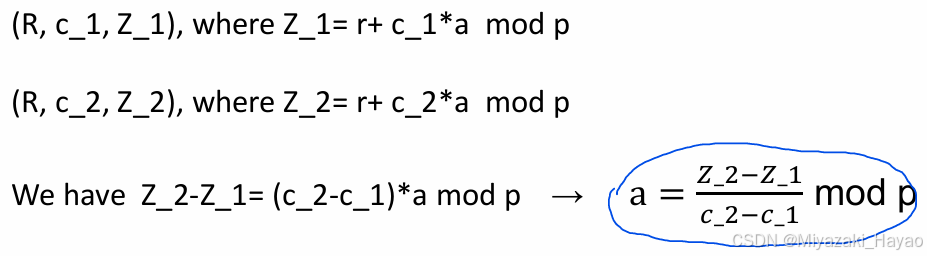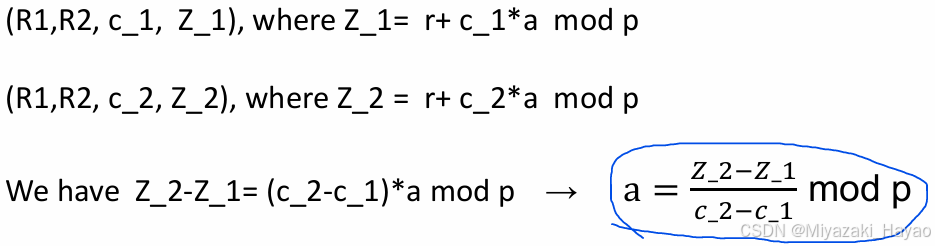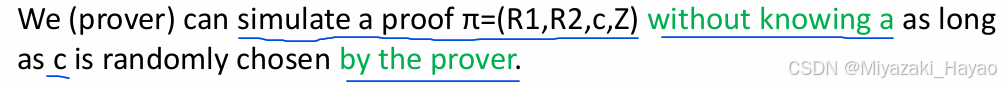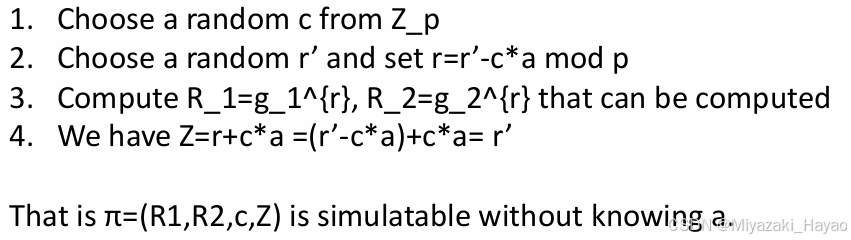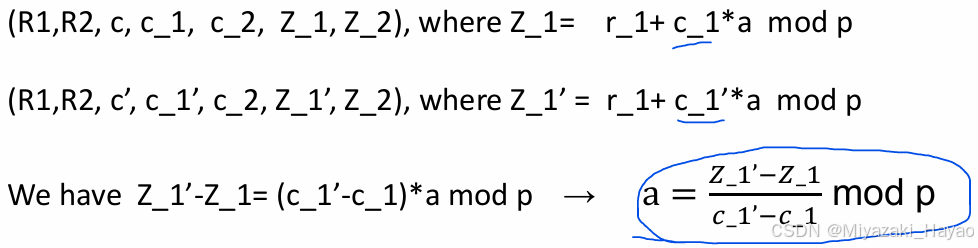文章目录
- 公钥加密之前的部分 (非重点,关注工具怎么用,和性质)
- 一、对称加密 (symmetric ciphers)
- 二、PRG (伪随机数生成器)
- 三、语义安全 (Semantic Security)
- 四、分组密码 (Block Cipher)
- 五、加密模型 (Encryption Modes)
- 六、Hash 函数
- 七、消息完整性 (Message Integrity)
- 八、验证加密 (Authenticated Encryption)
- 公钥加密及其之后的部分
- 九、公钥加密 (Public key encryption)
- 十、陷门函数 (Trapdoor function TDF)
- 十一、RSA
- 十二、ElGamal
- 十三、椭圆曲线上的计算问题
- 十四、数字签名 (Digital Signature)
- 十五、基于 陷门置换 的 FDH 签名
- 十六、基于 RSA 的 FDH 签名
- 十七、不基于随机预言机的安全签名
- 十八、零知识证明 (ZKP)
- 十九、Schnorr 的验证协议和签名协议
- 二十、承诺 Commitment
- 二十一、Oblivious Transfer (OT, 遗忘传输)
公钥加密之前的部分 (非重点,关注工具怎么用,和性质)
一、对称加密 (symmetric ciphers)
1. 定义
二、PRG (伪随机数生成器)
1. 定义
2. 属性
- 不可预测性
三、语义安全 (Semantic Security)
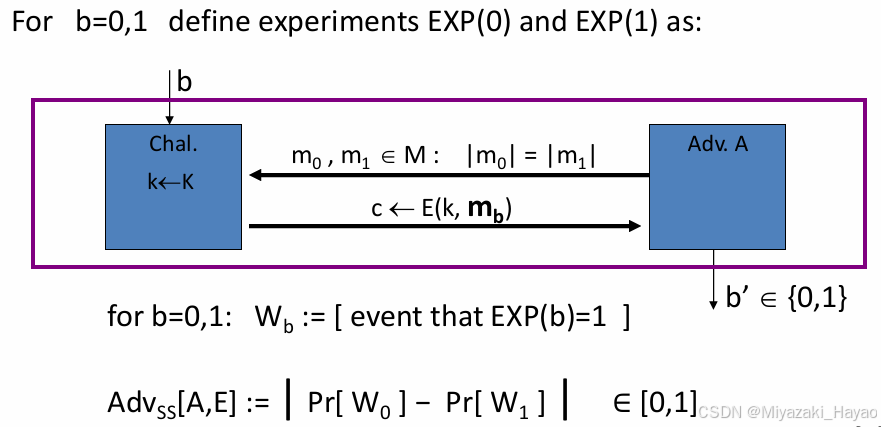
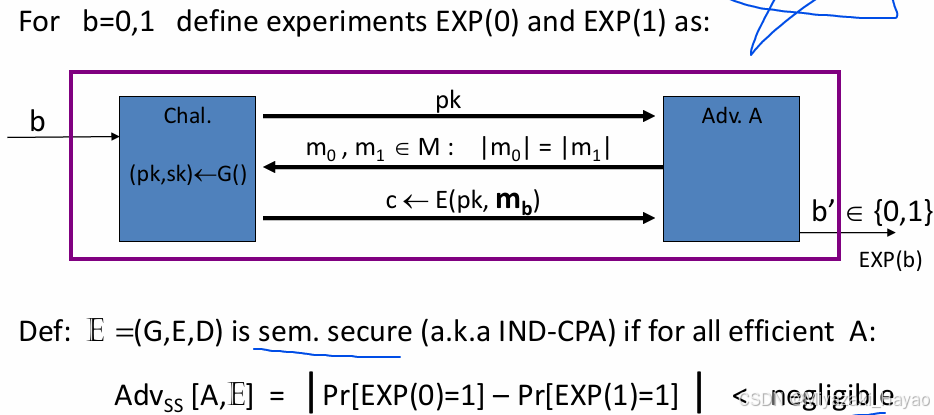
1. one-time key
攻击者发送明文给挑战者,挑战者根据 b 选择一条明文进行加密,并将生成的 密文c 发送给攻击者。攻击者需要更具 c 得到一个 b‘,如果 b’=b 则挑战成功,将其记为 EXP(b)=1。
将攻击者的优势记为
A
d
v
s
s
[
A
,
E
]
:
=
∣
P
r
[
W
0
]
−
P
r
[
W
1
]
∣
∈
[
0
,
1
]
Adv_{ss}[A,E]:=|Pr[W_0]-Pr[W_1]| \in [0,1]
Advss[A,E]:=∣Pr[W0]−Pr[W1]∣∈[0,1]。
2. 流密码是语义安全的
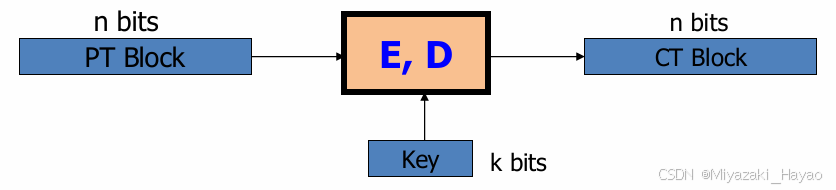
四、分组密码 (Block Cipher)
1. 工作模式
2. 迭代 (Iteration)
3. PRPs 和 PRFs
- PRF (Pseudo Random Function) defined over (K, X, Y):
F : K × X → Y F: K \times X \rightarrow Y F:K×X→Y - PRP (Pseudo Random Permutation) defined over (K, X):
E : K × X → X E: K \times X \rightarrow X E:K×X→X
PRF 从 X 中的元素 映射到 Y 中的元素 (如果 Y 就是 X,那么 PRF 就是 PRP)
PRP 从 X 中的元素 映射到 X 中的元素
- PRF 生成 PRG:
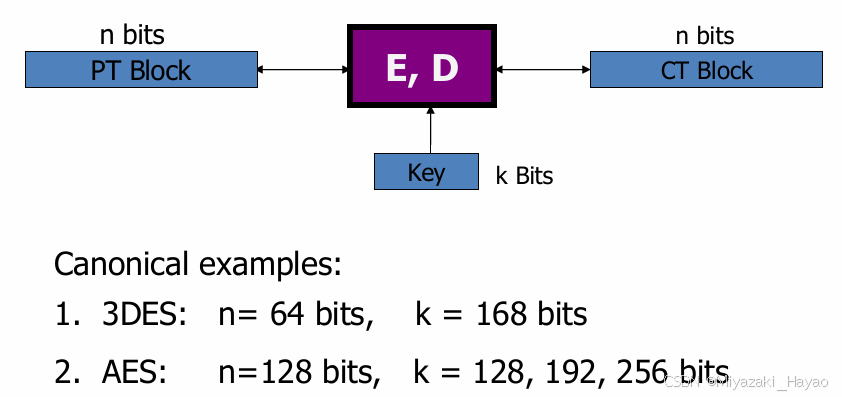
4. DES 和 AES
五、加密模型 (Encryption Modes)
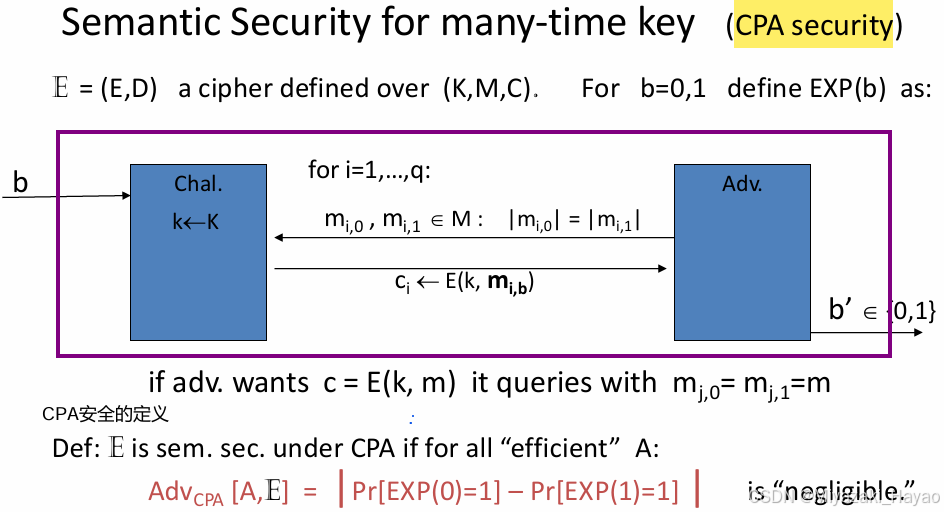
1. CPA secure model (for many-time key)
2. CCA secure model
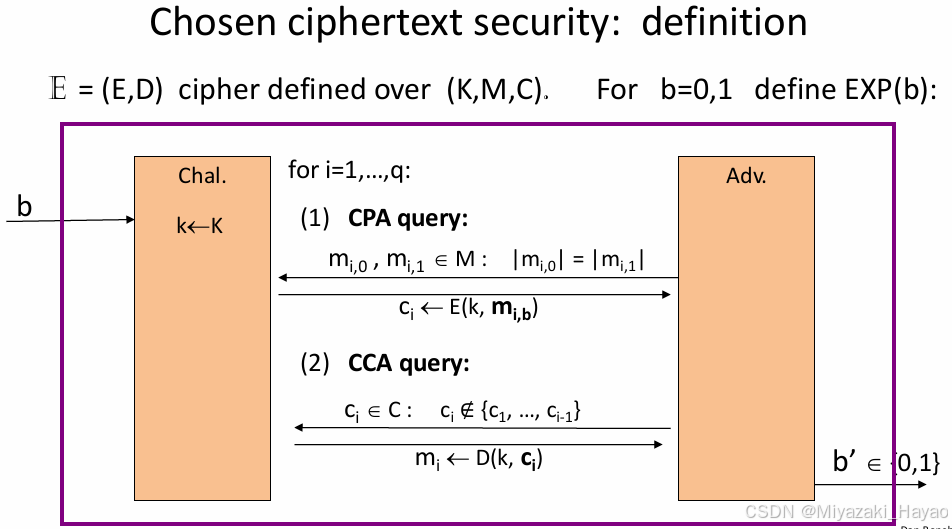
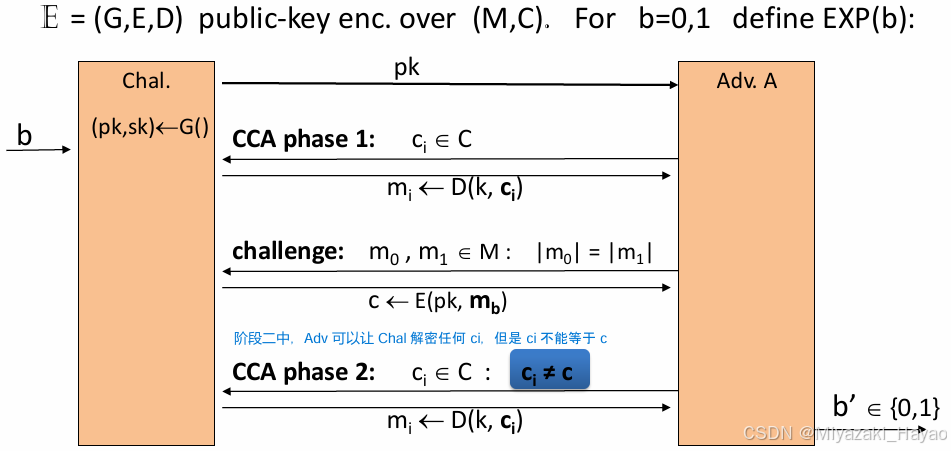
CCA 的定义是:攻击者可以选择 任意密文 并请求系统解密,得到 对应的 明文,但存在一个限制:攻击者无法请求解密 挑战密文 (challenge ciphertext),即测试语义安全性的密文不能被解密。
上面的整体过程是这样的:
- 首先,攻击者给挑战者发送了 i-1 组 mi,并且每一组挑战者都回复了对应的密文 ci;
- 到第 i 组的时候,攻击者给挑战者发送了两个明文 mi,0 和 mi,1,挑战者根据 b 对 mi,b 进行加密生成 ci 发送给攻击者;
- 然后攻击者可以给挑战者发送 密文c (图中的 CCA 阶段的 ci 和 上面 CPA 阶段的 ci 不是一个东西),挑战者给攻击者发送对 c 解密生成的 密文m (c 不能和 CPA 阶段生成的 密文 重复)。
- 最后 攻击者 需要通过上面得到的信息,推断出 ci 对应的 b 是多少,得到一个 b’,如果 b’=b 则攻击成功。
六、Hash 函数
1. Collision Resistance:
定义:给一个 Hash 函数 h : X → Y h: X \rightarrow Y h:X→Y,没有有效的机制,能够找到 x , x ′ ∈ X x, x' \in X x,x′∈X 满足 x ≠ x ′ , h ( x ) = h ( x ′ ) x \neq x', h(x) = h(x') x=x′,h(x)=h(x′)。
2. Second Pre-Image Resistance
定义:给一个 Hash 函数 h : X → Y h: X \rightarrow Y h:X→Y 和一个 x ∈ X x \in X x∈X,没有有效的机制,能够找到 x ′ ∈ X x' \in X x′∈X 满足 x ′ ≠ x , h ( x ′ ) = h ( x ) x' \neq x, h(x') = h(x) x′=x,h(x′)=h(x)。
3. Pre-Image Resistance
定义:给一个 Hash 函数 h : X → Y h: X \rightarrow Y h:X→Y 和一个 y ∈ Y y \in Y y∈Y,没有有效的机制,能够找到 x ∈ X x \in X x∈X 满足 y = h ( x ) y = h(x) y=h(x)。
4. 上面三个属性之间的关系
A imply B 的含义:如果一个加密系统满足 A 安全属性,那么它一定满足 B 安全属性。
5. Hash 函数被用来做什么
- 用来存储 password,服务器存储的是 h(pw) 而不是 pw。这是为了 安全性 (confidentiality)
- 用于 HMAC 中。这是为了 完整性
- 在 数字签名中,对 H(m) 签名 而不是 m。这是为了效率
七、消息完整性 (Message Integrity)
1. MAC (Integrity 但是不追求 Confidentiality)
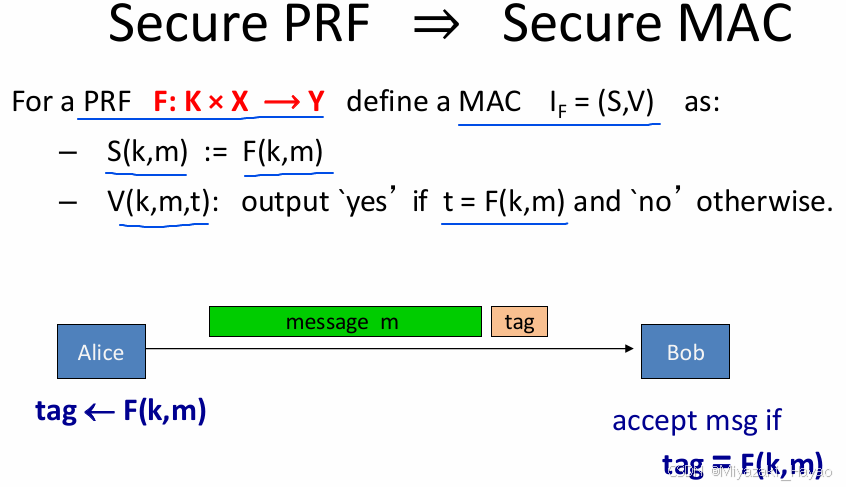
2. 基于 PRF 的 MAC
八、验证加密 (Authenticated Encryption)
1. 关于什么时候使用 MAC 和 Authenticated Encryption
- 如果消息需要的是 完整性 而不需要 保密性,则使用 MAC。
- 如果消息既需要 完整性 又需要 保密性,则使用 authenticated encryption。
2. 一个典型的模型
其中
D
:
K
×
C
×
N
→
M
U
{
T
}
D: K \times C \times N \rightarrow M U\{T\}
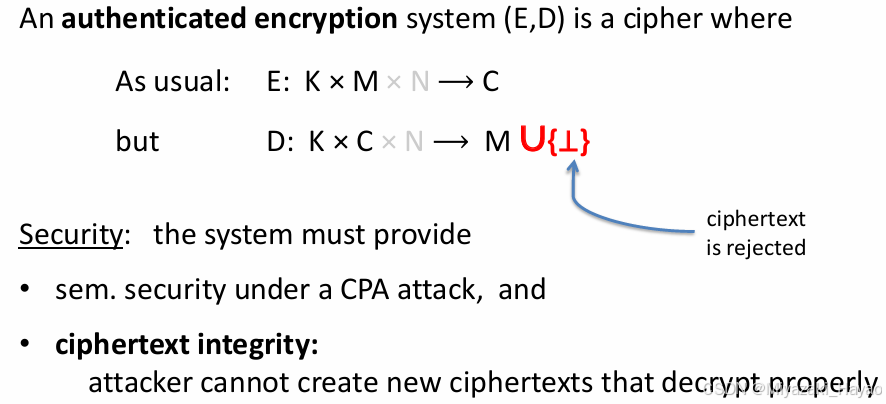
D:K×C×N→MU{T} 的含义是,如果 解密函数 检测到 密文c 被篡改或者不合法,就会输出 ⊥。特别强调了解密失败的状态,并表示系统具有 密文完整性 的能力,能够 拒绝伪造或篡改的密文。
3. 定义
一个密码 (E, D) 提供 authenticated encryption (AE),当满足:
- 满足 CPA 下的语义安全
- 具有密文完整性
4. Imply (在上面 hash 函数属性中有说)
公钥加密及其之后的部分
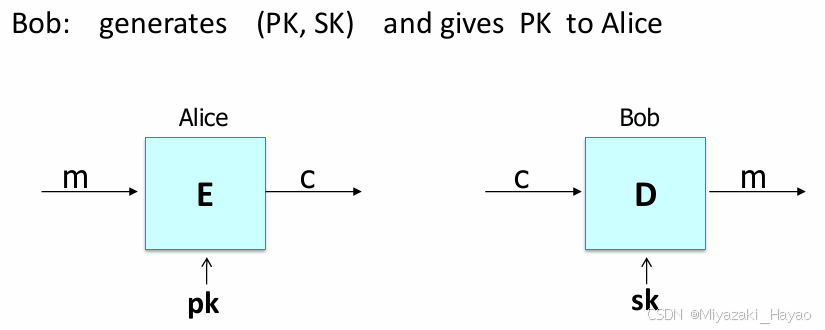
九、公钥加密 (Public key encryption)
1. 定义
2. 语义安全
3. 公钥密码的 CPA
回顾对称加密的两个安全概念:
- one-time security
- many-time security (也就是 CPA)
在 对称密码 中:
在 公钥密码 中:
4. 公钥加密的 CCA (chosen ciphertext security)
十、陷门函数 (Trapdoor function TDF)
1. 定义
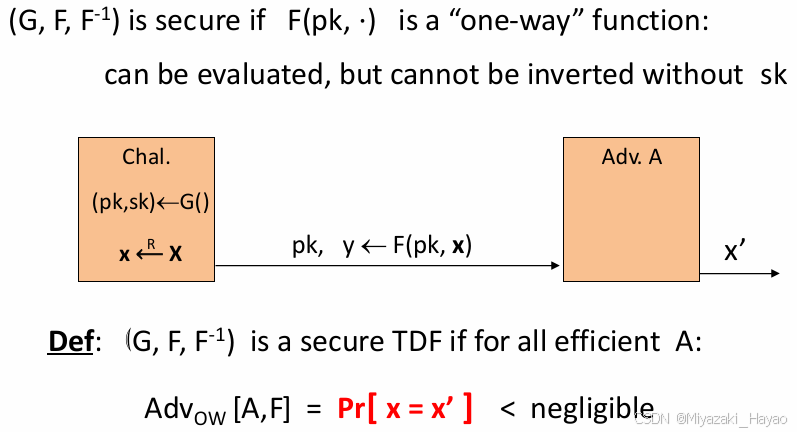
一个陷门函数 X → Y X \rightarrow Y X→Y 包含三个非常高效的函数:
- G ( ) G() G():输出一个密钥对 (pk, sk)。
- F ( p k , ⋅ ) F(pk,\cdot) F(pk,⋅):定义了一个函数 X → Y X \rightarrow Y X→Y。
- F − 1 ( s k , ⋅ ) F^{-1}(sk, \cdot) F−1(sk,⋅):上面那个函数的逆函数 Y → X Y \rightarrow X Y→X。
2. 安全性
3. 基于 TDFs 的 公钥密码
在上面的算法中,公钥密码 是用来处理 对称加密的 密钥 k 的,对 消息 的加密是通过 对称加密 完成的。
4. 基于 TDFs 的公钥密码的安全属性
十一、RSA
1. 算数模运算
2. RSA 公钥加密方案的基本步骤
- G() 密钥生成函数
- E(pk. m) 加密函数
- D(sk, (y, c))) 解密算法
具体步骤是:- 计算 x ← R S A − 1 ( y ) = y d = x e d = x x \leftarrow RSA^{-1}(y) = y^d = x^{ed} = x x←RSA−1(y)=yd=xed=x
- 计算 k ← H ( x ) k \leftarrow H(x) k←H(x)
- 用对称解密算法还原消息 m: m ← D s ( k , c ) m \leftarrow D_s(k,c) m←Ds(k,c)
3. RSA 的属性
- RSA 加密不是一个安全的加密系统!!
- RAS 加密快,解密慢。(Elgamal 则加密解密都相同)
十二、ElGamal
1. Diffie-Hellman 协议
2. 传统的 ElGamal
- Gen 密钥生成函数:
- 首先生成一个循环群 < G , q , g > <G, q, g> <G,q,g>
- 随机选取一个 x ∈ Z q x \in Z_q x∈Zq
- 计算 h : = g x h := g^x h:=gx
- 返回公钥和私钥,公钥为 p k = < G , q , g , h > pk = <G, q, g, h> pk=<G,q,g,h>,私钥为 s k = < G , q , g , x > sk = <G,q,g,x> sk=<G,q,g,x>
- Enc 加密算法:
- 输入一个 p k = < G , q , g , h > pk = <G, q, g, h> pk=<G,q,g,h> 和 消息 m
- 随机选取一个 y ∈ Z q y \in Z_q y∈Zq
- 对 m 进行加密, c t = < g y , h y ⋅ m > ct = <g^y, h^y \cdot m> ct=<gy,hy⋅m>
- Dec 解密算法:
- 输入一个 s k = < G , q , g , x > sk=<G, q, g, x> sk=<G,q,g,x>,和密文 c t = < c 1 , c 2 > = < g y , h y ⋅ m > ct = <c_1, c_2> = <g^y, h^y \cdot m> ct=<c1,c2>=<gy,hy⋅m>
- 对密文进行解密: m ^ = c 2 / c 1 x = h y ⋅ m / ( g y ) x = g x y ⋅ m / g x y = m \hat{m} = c_2 /c_1^x = h^y \cdot m / (g^y)x = g^{xy} \cdot m / g^{xy} = m m^=c2/c1x=hy⋅m/(gy)x=gxy⋅m/gxy=m
3. 现代的 ElGamal
首先设定一些前提:
- G G G:是一个阶为 n 的循环群
- ( E s , D s ) (E_s, D_s) (Es,Ds):是一个定义在 (K, M, C) 上的 对称AE 密码系统
- H : G 2 → K H: G^2 \rightarrow K H:G2→K:是一个哈希函数,例如 H ( u , v ) = k H(u, v) = k H(u,v)=k
接下来是算法的步骤 (核心思想就是,用 传统的ElGamal 加密 对称加密的密钥 k):
- 密钥生成函数:
- 从 G 中随机选取一个 生成元 g,随机选取一个 a ∈ Z n a \in Z_n a∈Zn
- 输出 s k = a , p k = ( g , h = g a ) sk = a, \ \ \ pk = (g, h = g^a) sk=a, pk=(g,h=ga)
- 加密算法:
- 随机生成 b ∈ Z n b \in Z_n b∈Zn
- 计算 u = g b u= g^b u=gb 以及 v = h b = g a b v = h^b = g^{ab} v=hb=gab
- 用 u 和 v 哈希得到一个 k,这是对称加密的密钥
- 通过对称加密加密消息 m, c = E s ( k , m ) c = E_s(k, m) c=Es(k,m)
- 输出 ( u , c ) (u, c) (u,c)
- 解密算法:
- 输入是 sk = a 和 加密时的输出 (u, c)
- 计算 v = u a = g a b v = u^a = g^{ab} v=ua=gab
- 计算出对称加密的密钥 k = H ( u , v ) k = H(u, v) k=H(u,v)
- 用 k 对 c 进行解密得到消息 m, m = D s ( k , c ) m = D_s(k, c) m=Ds(k,c)
4. 安全属性
(暂时没写)
十三、椭圆曲线上的计算问题
计算步骤如下:
- 问题背景:
- 第一步:
- 第二步:
- 第三步:
- 第四步:
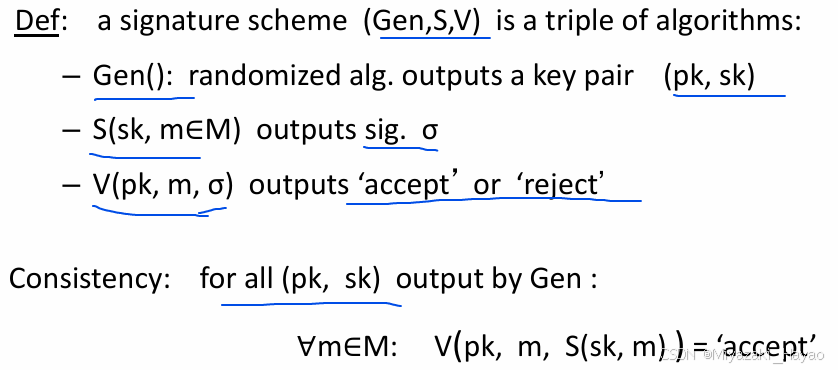
十四、数字签名 (Digital Signature)
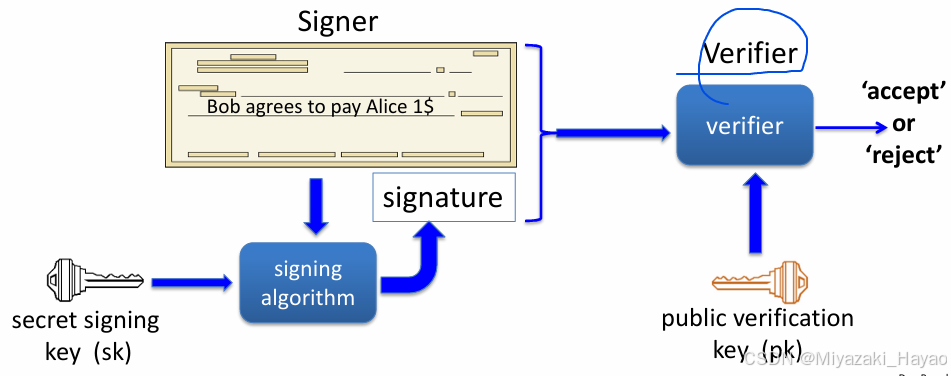
1. 基本过程
2. 定义
可以理解成 用 sk 进行加密,用 pk 进行解密。
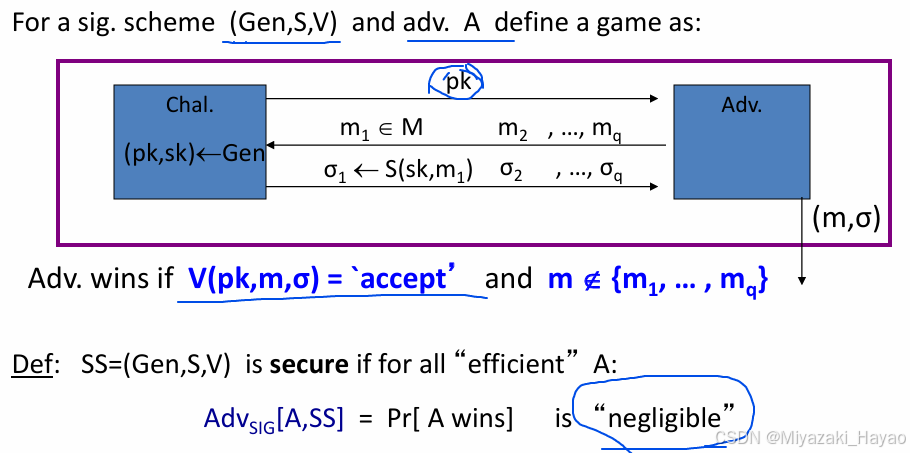
3. 安全属性
数字签名主要是保证 完整性、身份认证、防篡改。
注意,MAC 和 数字签名 都可以保证 完整性,但是通常:一对一的时候用 MAC,一对多的时候用 signature。
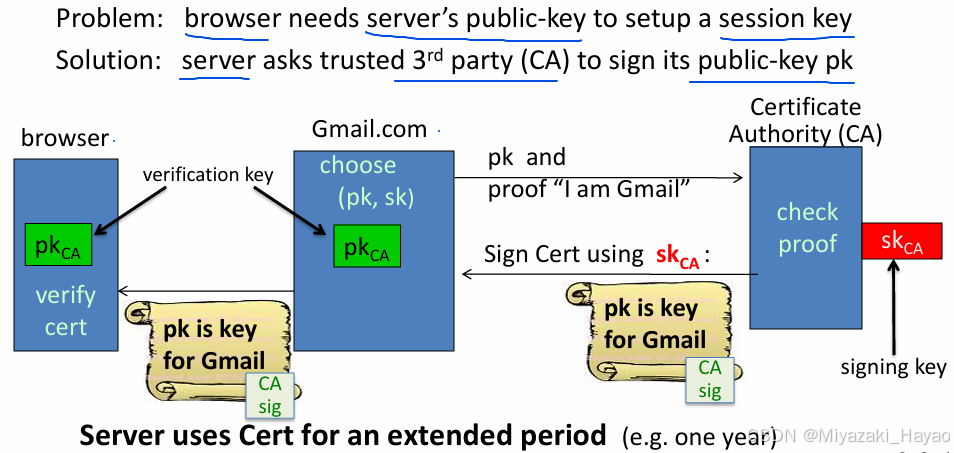
4. 应用 (证书 Certificates)
说明:
首先,浏览器 需要使用 服务器的 pk 来建立会话连接,需求是必须能 保证这个pk是服务器的pk 这件事。
对此的解决方法是,通过一个 第三方机构 CA 对 pk is key for Gmail 这个证书签名
所以对于上面的图,首先进行的是 Gmail.com 与 CA 之间的协议,生成一个具有 CA 签名的证书,该指数需要使用 pkCA 来验证。
然后,Gmail.com 将这个整数传给 浏览器。
5. 通过 CRHF 扩大域
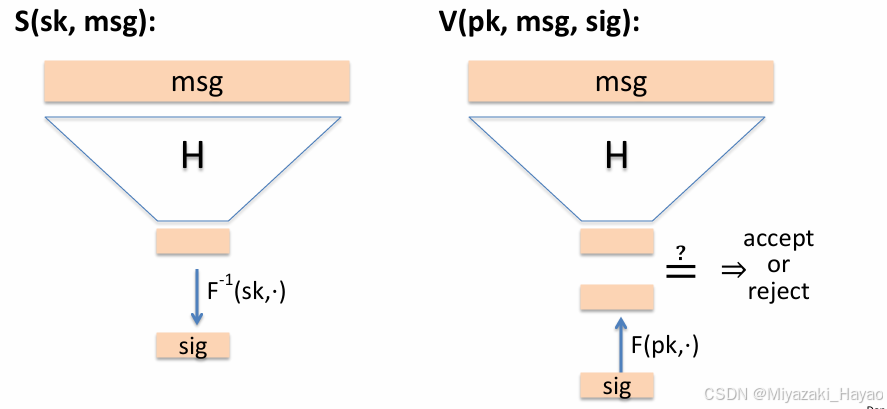
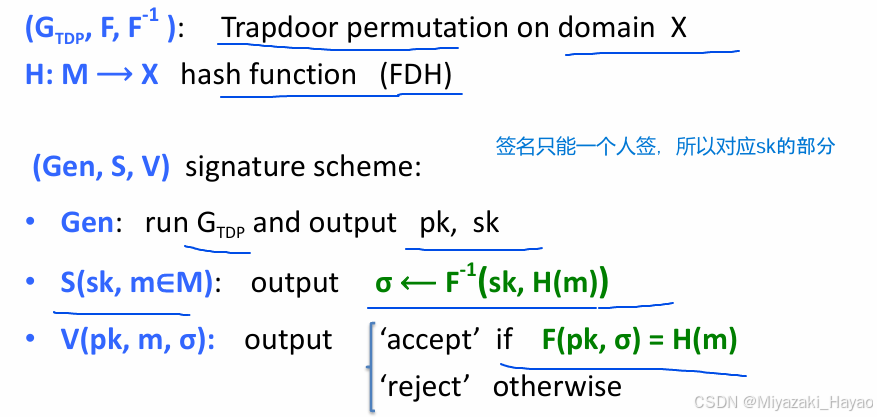
十五、基于 陷门置换 的 FDH 签名
FDH = Full Domain Hash
1. 示意图
2. 算法过程
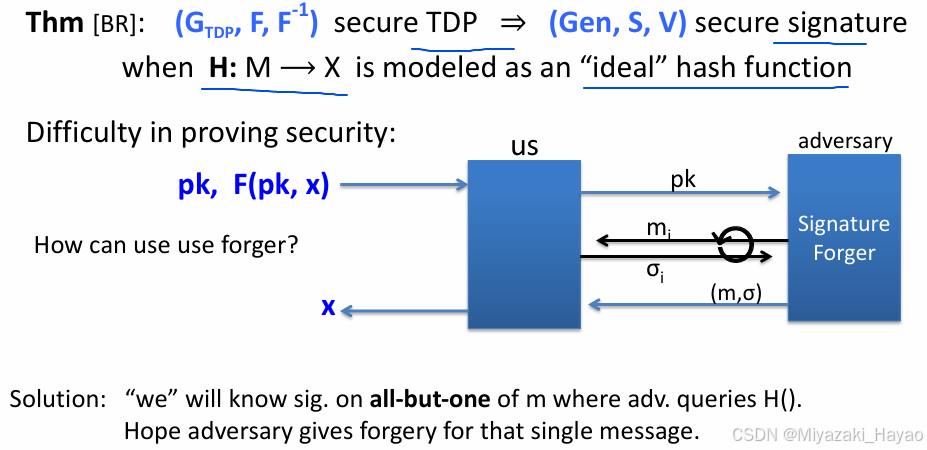
3. 安全性
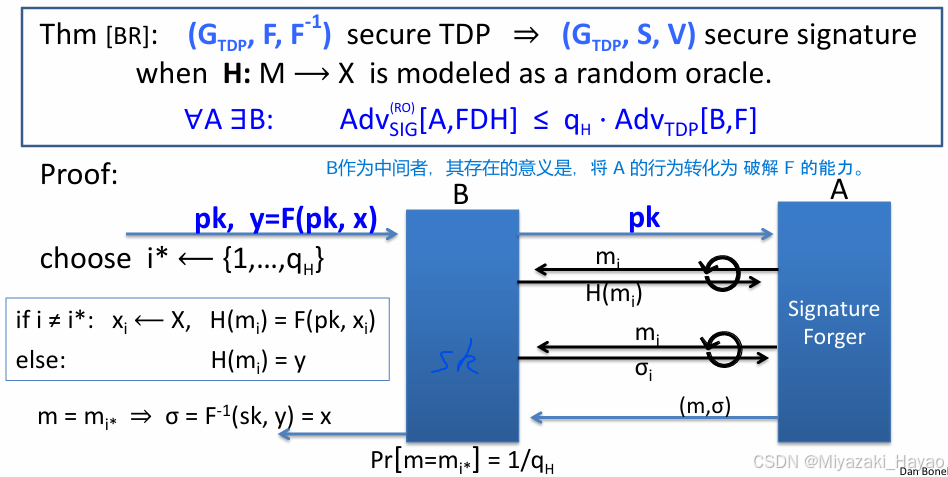
十六、基于 RSA 的 FDH 签名
1. 定义
2. 安全性证明
十七、不基于随机预言机的安全签名
1. 双线性对 (一个新的工具)
一个安全的签名如果不使用理想的哈希函数的话。可以使用 RSA 来替代,但是更多情况是通过 双线性对 来实现。双线性对的定义和主要性质如下:
- 定义:
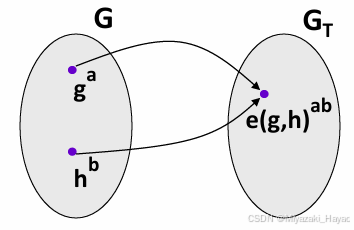
令 G , G T G, G_T G,GT 是两个有限循环群 G = 1 , g 1 , g 2 , . . . , g p − 1 G = {1, g^1, g^2, ..., g^{p-1}} G=1,g1,g2,...,gp−1。
定义一个匹配: e : G × G → G T e: G \times G \rightarrow G_T e:G×G→GT 是一个映射。 - 性质:
线性关系: e ( g a , h b ) = e ( g , h ) a b ∀ a , b ∈ Z g , h ∈ G e(g^a, h^b) = e(g, h)^{ab}\ \ \ \ \ \ \forall a, b \in Z\ \ \ \ g, h \in G e(ga,hb)=e(g,h)ab ∀a,b∈Z g,h∈G。
G 的生成元是 g,GT 的生成元是 (g, g)。
2. 基于双线性对的简单签名方案
3. 不基于 随机预言机 的签名方案
十八、零知识证明 (ZKP)
1. 关系函数 (Relation Function)
一个关系函数被定义为 R : X × Y → 0 , 1 R: X \times Y \rightarrow {0, 1} R:X×Y→0,1,满足:
- 该函数计算起来是高效的
- 输入是来自空间 (X, Y) 的一对元素 (x, y)
- 输出 0 表示 false,1 表示 true
例如:
| 场景 | 关系函数的定义 |
|---|---|
| Hash Function H | R ( x , y ) = 1 i f f H ( y ) = x ( N O T H ( x ) = y ) R(x, y) = 1\ iff\ H(y) = x\ \ \ (NOT\ \ H(x) = y) R(x,y)=1 iff H(y)=x (NOT H(x)=y) |
| Cyclic Group (G, g, p) | R ( x , y ) = 1 i f f g y = x ( ) R(x,y)=1\ iff\ g^y = x\ \ \ () R(x,y)=1 iff gy=x () |
2. 关系函数 R 下的语言
我们将 language L_R 定义为一组元素:
L
_
R
=
x
∈
X
:
t
h
e
r
e
e
x
i
s
t
s
y
s
.
t
.
R
(
x
,
y
)
=
1
L\_R = {x \in X: there\ exists\ \ y\ \ s.t.\ R(x, y) = 1}
L_R=x∈X:there exists y s.t. R(x,y)=1对于关系函数,有如下性质:
- 这是空间 X 的元素集合,如果 x 在 L_R 中,我们称 x 为一个 true statement。例如,R 被定义为基于 Hash 的关系函数。如果存在 y 满足 H(y) = x,则称 x 是一个 true statement。
- 给一个 x,判断 x 是否属于 L_R 是一个计算困难问题,这是因为如果 x 是一个 true statement,很难计算出一个 y 使得 R(x, y) = 1。
3. 交互式证明系统
一个交互式证明系统包括两个角色 Prover 和 Verifier。Prover 的输入是 (x, y),Verifier 的输入是 (x)。
4. 三个属性
- Completeness (知道 输入y 和 输出x)
如果 Prover 知道 (x, y),存在一个证明 π 满足 V e r i f i e r ( x , π ) = 1 Verifier(x, π) = 1 Verifier(x,π)=1。
等价于,我们构造证明来证明它满足这个性质。 - Soundness (知道 输出x,难算 输入y)
如果 Prover 只知道 (x),对于 Prover 来说计算出满足 V e r i f i e r ( x , π ) = 1 Verifier(x, π)=1 Verifier(x,π)=1 的 π 是一个计算困难问题。
等价于,我们可以通过 rewind 的方式从证明中提取知识。 - Zero Knowledge (知道 输入y 和 输出x)
Verifier 对于 π,除了 x 之外一无所知。
等价于,我们可以在 不知道 y 的情况下模拟证明。
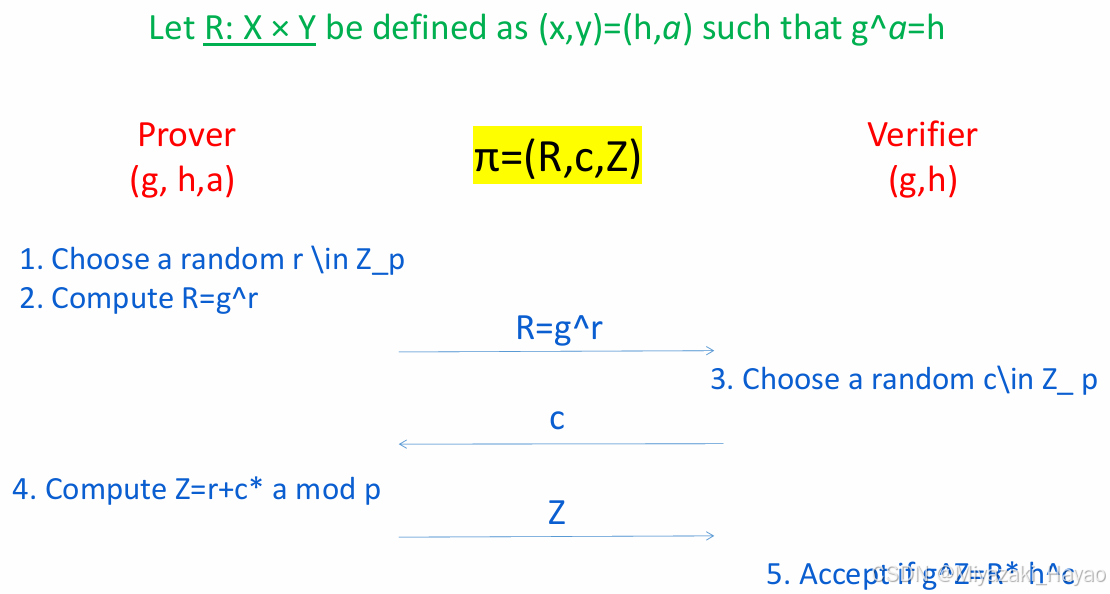
4. sample 1 (定义 (x, y) = (h, a) 为 ga = h)
- Completeness
- Soundness (下面就是 rewind 过程)
- Zero-Knowledge (可以将第二部的 r’ 换成 Z’)
5. sample 2 (and 证明)
- Completeness
- Soundness
- Zero-Knowledge (可以将第二部的 r’ 换成 Z’)
6. sample 3 (or 证明)
-
Completeness
-
Soundness
-
Zero-Knowledge
十九、Schnorr 的验证协议和签名协议
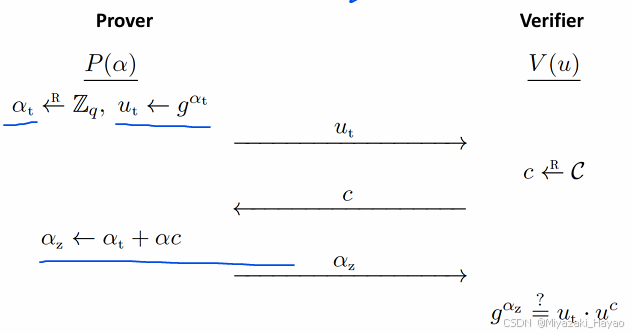
1. Schnorr 的验证协议
可以发现 Schnorr 的验证协议和 ZKP 的 sample 1 很像,可以一起记。
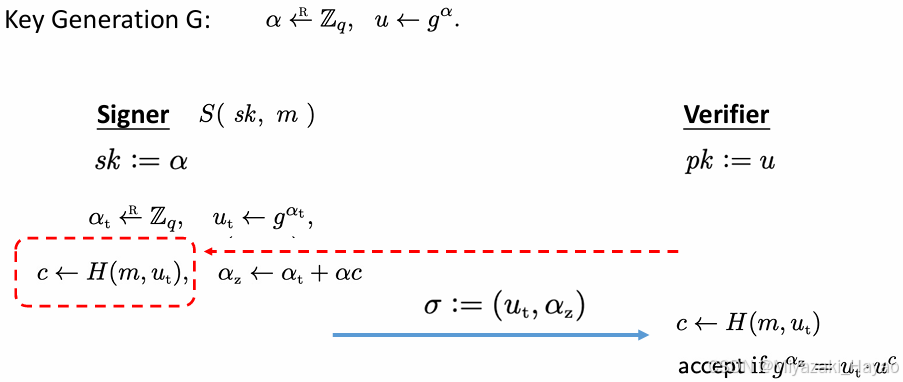
2. Schnorr 的签名方案
schnorr 的签名方案实际上就是基于上面所讲的 schnorr 的认证协议改过来的。
这里的 H(m, ut) 的作用就是将 交互式 变成 非交互式,在上面的 ZKP 中,也可以用同样的方式改为非交互式的 ZKP。
只需要注意,在 ZKP 中,如果不需要签名,则 H() 函数中 不需要 加入 m 参数,直接 c=H(ut) 即可。
二十、承诺 Commitment
1.基本概念
承诺方案是一种加密原语,允许一个人承诺一个选定的值 (或选定的语句),同时对其他人 隐藏 它,并能够在 稍后显示承诺的值。
承诺方案的设计使得 一方在 承诺之后 无法更改价值或声明 (也就是不允许反悔)。
承诺方案包括两个部分,发送者和接收者之间的承诺方案由两种算法组成:
- Commit(m):
将要承诺的值 m 作为输入,运行 PPT 算法,该算法返回 承诺 C 和 秘密 r (C 将会传给接收者)。 - Open(C, m, r):
以 (C,m,r) 作为输入,运行 PPT 算法来 验证 承诺是否在 m 上。
2. 安全要求 (Hinding 和 Binding)
- Hinding
给定 (C,m0, m1),从计算上很难猜测 C 承诺的消息是 m0 还是 m1。 - Binding
给定 C,用两个不同的消息 (m1,r1) 和 (m2,r2) 打开这个承诺 C 在计算上很困难。
3. 一个安全的承诺方案
首先设 (g, h) 是两个群元素,由 receiver 选择的。
- Commit(m):
输入是 m ∈ Z p m \in Z_p m∈Zp,随机选择一个 r ∈ Z p r \in Z_p r∈Zp,并计算:
C = g m h r , s e c r e t = r C = g^m\ h^r, secret = r C=gm hr,secret=r - Open(C, m’, r’):
输入是 ( C , m ′ , r ′ ) (C, m', r') (C,m′,r′),如果满足下面等式,则返回 accept:
C = g m ′ h r ′ C = g^{m'}\ h^{r'} C=gm′ hr′
4. 证明上面的承诺方案的安全性
(略,在ppt上)
二十一、Oblivious Transfer (OT, 遗忘传输)
1. 定义
在 OT 协议中,参与的有两方,发送方和接收方。
该协议的目的在于,让发送方不知道发送给接收方的消息是什么消息。这个问题可以转化为:发送方不知道接收方接收了哪条消息。
一个很直接的实现方法就是,发送方发送很多条消息给接收方,接收方从中选择自己要接收的消息,这样发送方就不知道接收方接收的是哪条消息了。
值得注意的是,接收方除了 M_i 什么都不知道。
2. ElGamal Encryption (PKE)
3. 1-out-of-2 OT
基本过程 (下面对 M1 和 M2 的加密使用的是上面提到的 ElGamal Encryption):
4. 1-out-of-n OT
5. k-out-of-n OT
就是将上面的 1-out-of-n OT 执行 k 次。