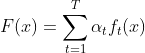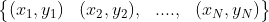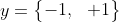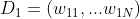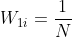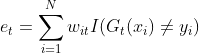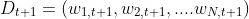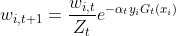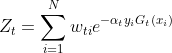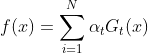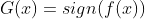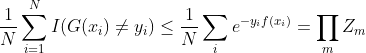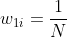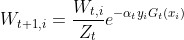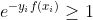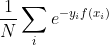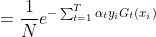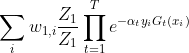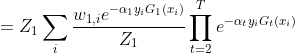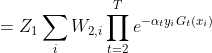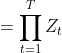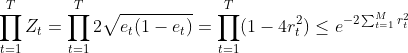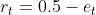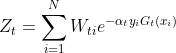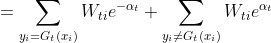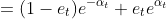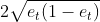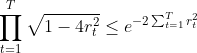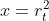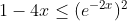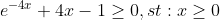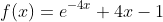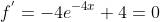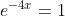前言:
Boosting 是一种集成学习方法,它由多个弱分类器组成(准确率>50%)。预测时,用若分类器分别进行预测,然后投票得到结果。 相对随机森林是样本随机抽样构造的训练集,Boosting 更关注被前面弱分类器错分的样本。
AdaBoost 由Freund等人提出,是Boosting算法的一种实现版本。
最后给出乳腺癌分类的例子
目录
- 算法简介
- 算法流程
- 误差分析
- 例子
一 算法简介:
AdaBoost 算法全称自适应Boosting 算法(Adaptive Boosting)是一种二分类问题的算法。
通过弱分类线性组合来构造强分类器。 强分类器计算公式为:
每个弱分类器输出值为: +1,-1
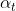
T: 弱分类器个数
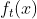
相对投票算法KNN, 多了一个权重系数
二 算法流程:
输入:
训练数据集
弱学习算法
N: 样本个数
T: 总的学习器个数
1 初始化训练数据集权值分布:
其中
2: t =1,2,...T
a
b: 计算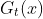
c: 计算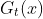
对数是自然函数
d: 更新训练数据集的权值分布
其中Zm 是归一化因子
3: 构建资本分类器的线性组合
得到最终分类器
三 训练误差分析
定理1: AdaBoost 算法最终分类器的训练误差界为:
预设条件:
证明:
当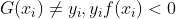
所以
=
在每轮选择合适的Gt可以使得Zt最小,从而下降也最快
定理2 (二分类问题 AdaBoost 训练误差界)
其中
证明:
=
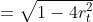
说明每个弱分类器,误差越小越好
其中
可由 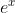
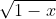
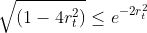
证明:
令
即要证明
即要证明:
令
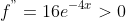
极小值就是驻点
x=0 点也满足约束条件
所以f(x)=1+0-1>=0
上面不等式也可以由
推论: 如果存在r>0,对所有的T 有 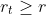
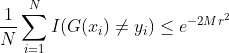
四 例子 (乳腺癌分类)
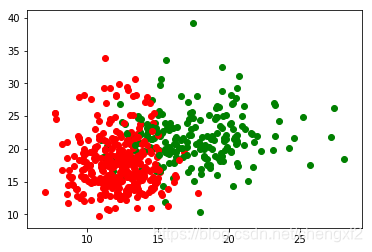
数据集
训练结果
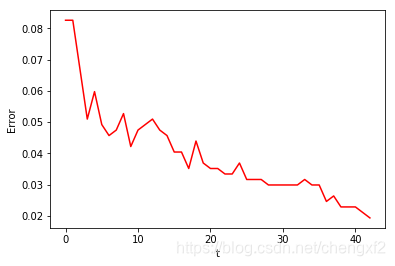
错误率随着弱分类器个数增加而减小
# -*- coding: utf-8 -*-
"""
Created on Mon Nov 25 14:42:22 2019
@author: chengxf2
"""
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
class AdaBoost:
def DrawScatter(self, dataMat, labelMat):
m,n = np.shape(dataMat)
for i in range(m):
x1 = dataMat[i,0]
x2 = dataMat[i,1]
y = labelMat[i,0]
if np.sign(y)>0:
plt.scatter(x1,x2,c='r')
else:
plt.scatter(x1,x2,c='g')
plt.show()
"""
计算alpha:
Args
e: 未分类的样本数目/所有样本
"""
def CalcAlpha(self, e):
epsilon = np.log((1-e)/e)/2.0
return epsilon
"""
加载数据集
Args
None
return
None
"""
def LoadSimpData(self):
cancer = load_breast_cancer()
self.dataMat = np.mat(cancer.data) #(569,30)
self.classLabels = np.mat(cancer.target).T #(569,1)
self.m, self.n = np.shape(self.dataMat)
for i in range(self.m):
if self.classLabels[i,0]<1:
self.classLabels[i,0]=-1
self.W = np.ones((self.m,1))/self.m
#print("\n LoadSimData: \t",self.classLabels)
self.DrawScatter(self.dataMat, self.classLabels)
"""
单个分类器
Args
dataMat: 数据
dimen: 维度
thresh: 阀值
Less: True else >
return
retMat
"""
def stumpClassify(self, dataMat, dimen, thresh, less):
m,n = np.shape(dataMat)
retArray = np.ones((m,1))
if less:
retArray[dataMat[:,dimen]<=thresh]=-1.0
else:
retArray[dataMat[:,dimen]>thresh]=-1.0
#print("\n retArray ",retArray)
return retArray
def __init__(self):
self.m = 0 ##样本个数
self.n = 0 ##样本维度
self.T = 5 ##基分类器个数
self.W = None ##样本分布权值
self.LoadSimpData()
self.minError = 0.02
"""
创建基分类器
Arg
None
return
弱分类器
"""
def BuildStump(self,W):
numSteps = 20.0
bestStump ={}
minErr = np.inf
for i in range(self.n):
rangeMin = min(self.dataMat[:,i])
rangeMax = max(self.dataMat[:,i])
stepSize =(rangeMax - rangeMin)/numSteps
#print("\n ***************\n ","\t rangeMin: ",float(rangeMin),"\t max: ",float(rangeMax))
for j in range(int(rangeMin), int(numSteps)+1):
for ls in [True, False]:
thresh = float(rangeMin+ j*stepSize)
#print("\t j: ",thresh)
retLabel = self.stumpClassify(self.dataMat, i, thresh, ls)
errArr = np.mat(np.ones((self.m, 1)))##错误
errArr[retLabel == self.classLabels] =0 #相等就不计数
weightErr = np.dot(W.T,errArr)
#print("\n weightErr : ",weightErr)
if float(weightErr)<minErr:
bestStump['dim'] =i
bestStump['thresh']=thresh
bestStump['ls'] = ls
minErr = float(weightErr)
bestClass = retLabel.copy()
#print("\n minErr", minErr, "\n bestSump ",bestStump)
return bestStump, minErr,bestClass
"""
集成学习
Args
numIt: 弱分类器个数
return
weakClass: 弱分类器
"""
def adaBoostTrain(self, numIt):
W = np.mat(np.ones((self.m, 1)))/self.m
boostClass =np.mat(np.zeros((self.m , 1)))
weakClass =[]
one = np.ones((self.m, 1)) ##统计错误个数得矩阵
ErrList =[]
for t in range(numIt):
bestStump, error, classEst= self.BuildStump(W)
#print("\n *********t**********:\n \t t: ",t,"\t:error ",error)
if error>0.5:
break
alpha = self.CalcAlpha(error)
bestStump['alpha']= alpha
weakClass.append(bestStump)
yg = np.multiply(-1*alpha*self.classLabels, classEst)
W = np.multiply(W, np.exp(yg))
W = W/W.sum()
# print("W, ",W)
##########错误累加计算#########3
boostClass += alpha*classEst
boostError = np.multiply(np.sign(boostClass)!= self.classLabels, one)
errorRate = boostError.sum()/self.m
print("\n t: ",t, "\t errorRate ",errorRate)
#print("\n boostError ",boostError)
ErrList.append(errorRate)
if errorRate<self.minError:
break
print("\n errorRate", errorRate,"\n ******weakClass******* \n",weakClass, " 弱分类器个数 ",t)
x = np.arange(0, len(ErrList))
plt.plot(x, ErrList, c='r')
plt.xlabel("t")
plt.ylabel("Error")
return weakClass
ada = AdaBoost()
ada.adaBoostTrain(200) 参考文档
《统计学习方法》
《机器学习与应用》