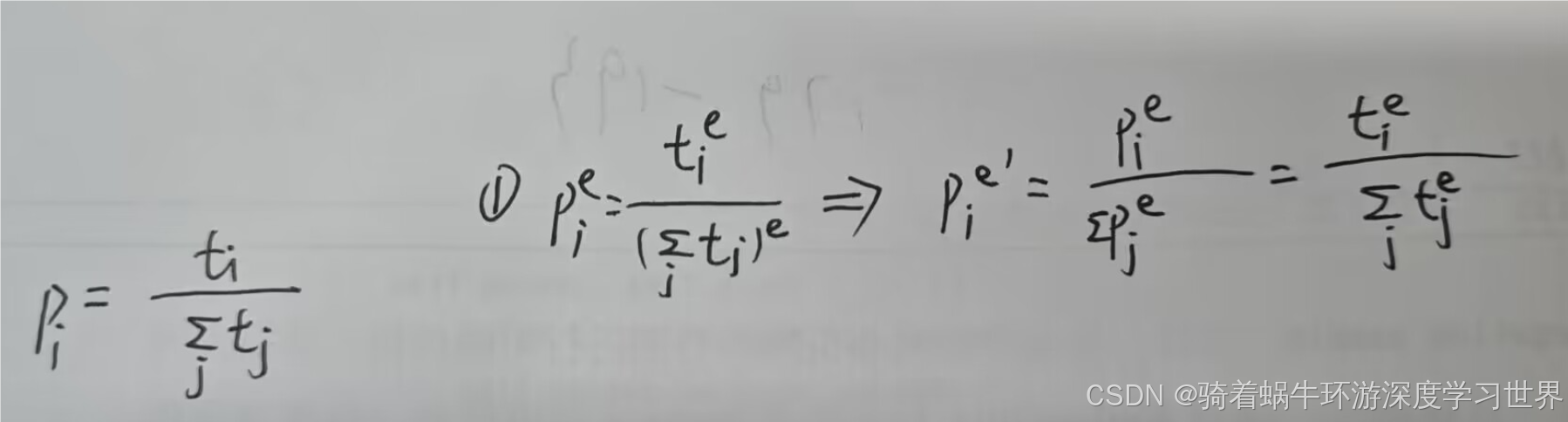Bootstrap

1.8-word2vec的改进

文章目录

1问题分析一

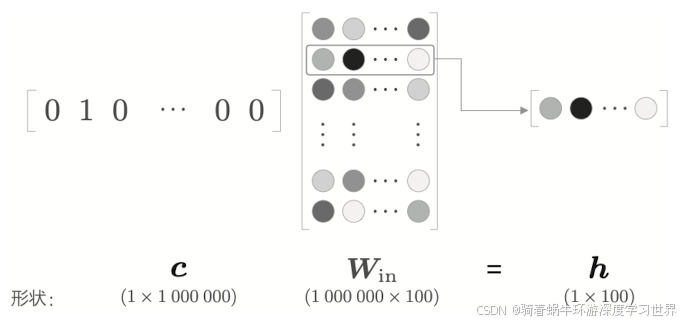
  1. 问题主要是在计算量上；前面讲述的CBOW模型、skip-gram模型的代码实现，输入都是用的独热编码，然后将独热编码与输入侧权重矩阵 w i n w_{in} win​相乘；
  2. 独热编码将单词都转换为固定长度的向量，固定长度既是好处也是坏处，按照独热编码的构成方式，坏处就是当语料库中的单词很多时，每个独热编码向量都很长；
  3. 用很长的独热编码向量与权重矩阵 w i n w_{in} win​相乘，这也要花费很多的计算资源；
  4. 这种问题的解决方法是换成Embedding层。即直接从权重矩阵 w i n w_{in} win​中选择特定行传递到下一层。

2改进一之Embedding层

2.1 Embedding层的实际作用

  1. 上述使用独热编码表示输入，然后与输入侧权重矩阵 w i n w_{in} win​相乘，本质上是从输入侧权重矩阵 w i n w_{in} win​中选择了某一行（因为独热编码只有一个元素为1，其余元素为0），如下图所示：

    在这里插入图片描述

  2. 因此我们好像就没有必要用一个矩阵乘法来实现“选取某一行”这样的过程，毕竟我们能够知道这个乘法本质上是取一行出来，但是计算机不知道，他只知道我们给他了一个向量和一个矩阵，他会老老实实的去计算乘法；

  3. 因此这里改进之后的Embedding层的作用就是：从权重参数中抽取“单词 ID 对应行(向量)”；

2.2数组切片获取某行的操作

  1. 使用numpy.arange方法构建一个序列，并将其形状转为(7,3)；我们可以通过切片的方法来获取某一行，如下所示；

    W = np.arange(21).reshape(7, 3)
W[2]
W[5]

  2. 想要获取多行则只需要构建一个需要索引出来的行号数组，然后用同样的切片方法即可，如下所示；这种实现的可能性允许我们进行mini-batch的处理；

    idx = np.array([1, 0, 3, 0])
W[idx]

  3. 有了上面的方法，就可以实现Embedding层的前向传播过程了。

2.3 Embedding层的实现

  1. 这里实现的embedding层就跟我们在pytorch里面使用的torch.nn.Embedding【示例】很像了：
    1. torch.nn.Embedding需要传入两个参数，一个是vocab_size，一个是emb_size；
    2. 而这里Embedding层的参数就是输入侧的权重矩阵，维度其实就是[vocab_size,emb_size]；
  2. 代码位置：utils\Embedding.py；

2.3.1初始化

  1. 和前面实现矩阵相乘的MatMul类一样，初始化时需要保存该层的参数和梯度为类的成员变量

    1. 参数就是上面说的权重矩阵 w i n w_{in} win​；
    2. 梯度自然就是和一样的数组了；
    3. 为了后面整合所有层的参数的方便，这里和之前一样，参数和梯度都是最终保存在了列表中；
    4. 另外，使用idx保存需要提取的行的索引的数组；便于在反向传播时来更新权重矩阵 w i n w_{in} win​中对应的行的参数的梯度；
    class Embedding:
    def __init__(self, W):
        self.params = [W]
        self.grads = [np.zeros_like(W)]
        self.idx = None

2.3.2前向计算

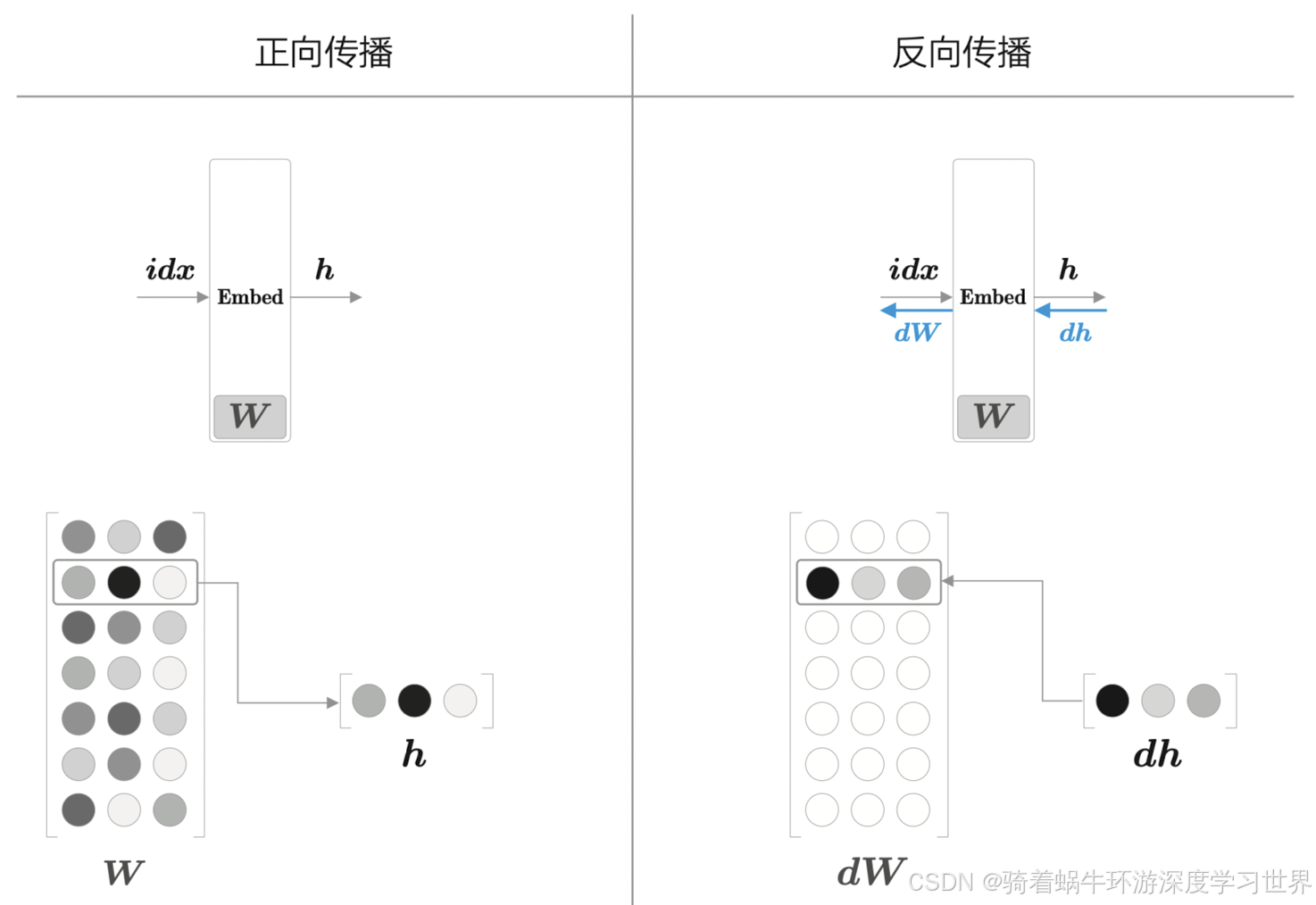
  1. 前向计算本质上就是从权重矩阵 w i n w_{in} win​中根据需要抽取特定的行，并将该特定行的神经元原样传给下一层；在本示例中就是传递给中间层；所以直接使用切片的方式根据idx的值获取W中特定的行即可；

    def forward(self,idx):
    W, = self.params
    out = W[idx]
    self.idx = idx
    return out

2.3.3反向传播

  1. Embedding层只是从矩阵中抽取了特定的行给到下一个层，因此当前面的梯度反向传播到此处时，不需要进行任何计算，直接就是权重矩阵 w i n w_{in} win​中对应参数的梯度；

  2. 由于是选取了某一行传递到后面的层，因此梯度应该落到特定行上（此时self.idx将起到作用），如下图所示；

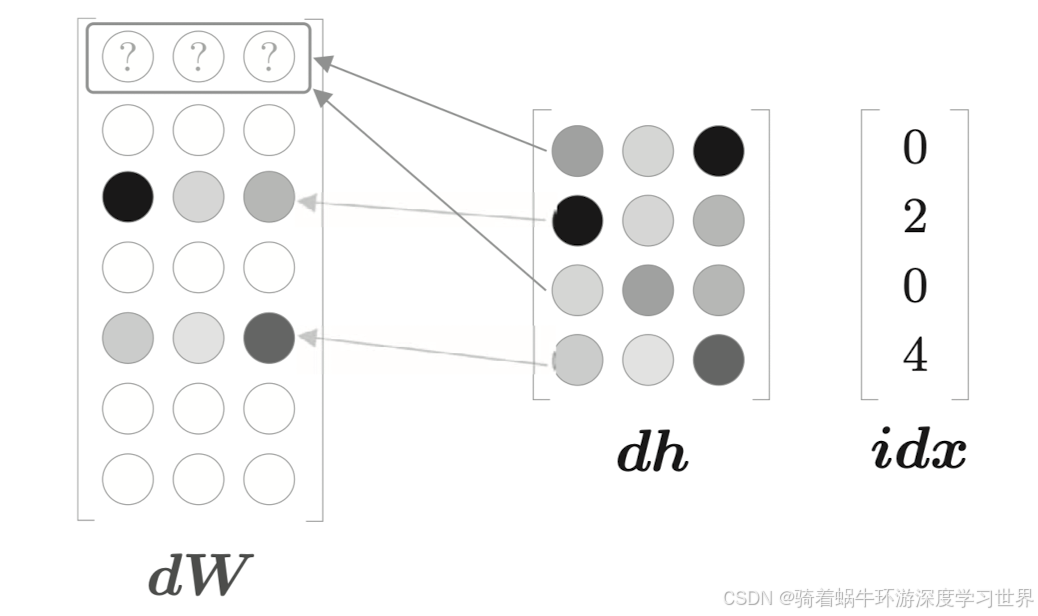
    在这里插入图片描述

  3. 当idx中有重复索引时，选择的是权重矩阵 w i n w_{in} win​​中的同一行，这一行在后面的层将被计算多次；这种情况相当于这一行向量被复制形成了分支；那么根据之前的经验，梯度反向传播时梯度应该被累加；如下图所示；

    1. 什么情况下会重复：
      1. 对于CBOW模型，输入只有中间的目标词，那么如果一个句子里面不小心一个单词被重复了两次则符合这种情况，例如I love love you；
      2. 对于skip-gram模型，输入是上下文窗口范围内的单词，那这个范围可大可小，因此必然是有重复单词出现的可能性的。

    在这里插入图片描述

  4. 代码如下：

    1. 主要是np.add.at(dW, self.idx, dout)方法的使用：根据self.idx将dout加到dW的对应位置处；
    2. 该方法既可以加到特定横纵坐标处，还可以加到特定行的所有元素上，可见该方法的灵活；
    3. 也可以使用for循环来实现梯度的累加，但是速度上没有numpy库2快；
    def backward(self, dout):
    dW, = self.grads
    # 由于书中的adam优化器更新参数时是每个参数都去更新，因此这里权重矩阵的梯度形状设置为了与权重矩阵一样
    dW[...] = 0
    # 一个示例
    # dW:[7,3]
    # idx:[0,2,4,6]
    # dout:[[0.1,0.2,0.3],[0.1,0.2,0.3],[0.1,0.2,0.3],[0.1,0.2,0.3]]
    np.add.at(dW, self.idx, dout)
    return None

3问题分析二

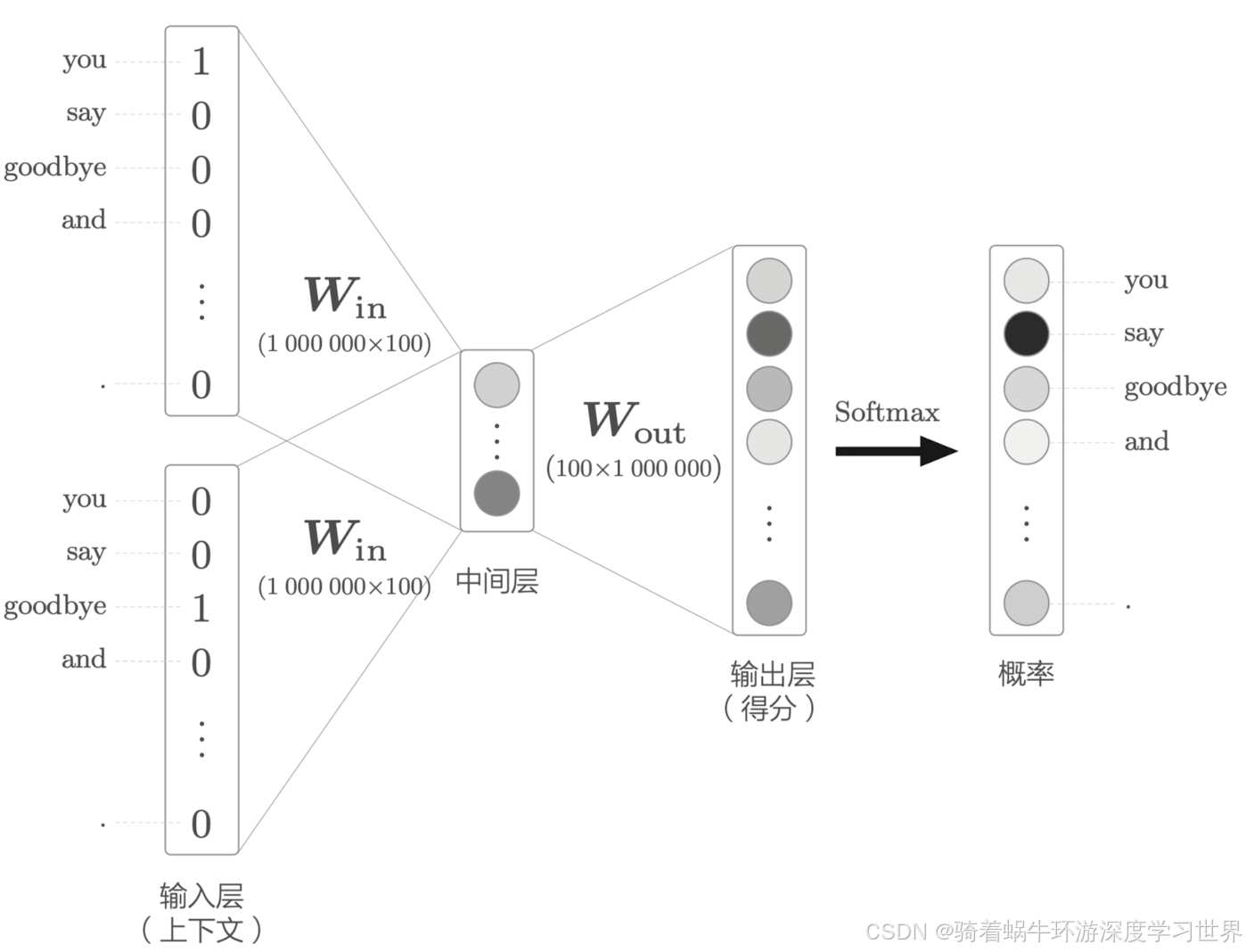
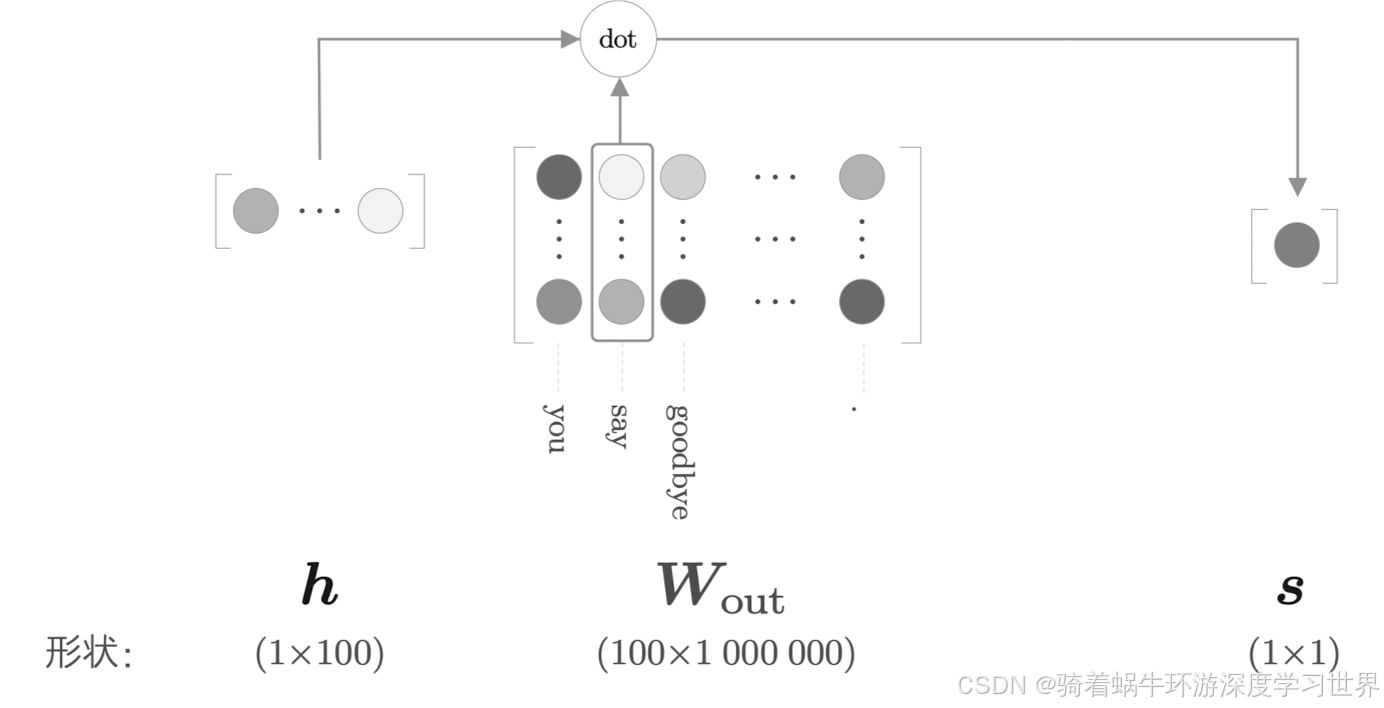
  1. 第二个问题就是中间层之后与权重矩阵 w o u t w_{out} wout​​的乘积运算，如下图所示，同样是维度太大的问题；输入侧的矩阵乘法运算是分析了独热编码向量的特点之后做出了Embedding层的改进方法的；

    在这里插入图片描述

  2. 另外，中间层结果与权重矩阵 w o u t w_{out} wout​的乘积运算之后还有softmax的计算，这个概率化的计算方法需要每个元素都求一次指数，因此当语料库非常大的时候，这个计算量也是巨大的。

  3. 还记得之前我们刚开始学习CBOW模型时讲到，选取模型结构中的哪个作为单词的分布式表示吗；其实是可以用权重矩阵 w o u t w_{out} wout​作为分布式表示的，只不过这个时候应该是每一列代表一个单词的分布式表示，即上图中1000000这个维度；

  4. 权重矩阵 w o u t w_{out} wout​每一列表示语料库中一个单词，因此可以单独取出每一列，对每一列做一个二分类问题；接下来我们详细看一下这第二个问题的解决办法。

4改进二之将多分类变为二分类

  1. 改进的思想主要为：
    1. 以CBOW模型为例，比如我们要预测的是中间词是否为say，则可以直接从权重矩阵 w o u t w_{out} wout​中取出say对应的列向量，与中间层的输出做内积得到一个标量，然后就可以做一个简单的二分类问题
    2. 但这还只是让模型去学习了如何尽可能预测正确的情况，还得让模型学习如何尽可能将其他单词预测为负样本（即让模型知道其他单词不是正确的单词）的情况，此时则引入了负采样的方法。

4.1二分类问题

  1. 在多分类的情况下，输出层使用 Softmax 函数将得分转化为概率，损失函数使用交叉熵误差。在二分类的情况下，输出层使用 sigmoid 函数， 损失函数也使用交叉熵误差（但是是二分类的交叉熵公式，与之前的稍有区别）

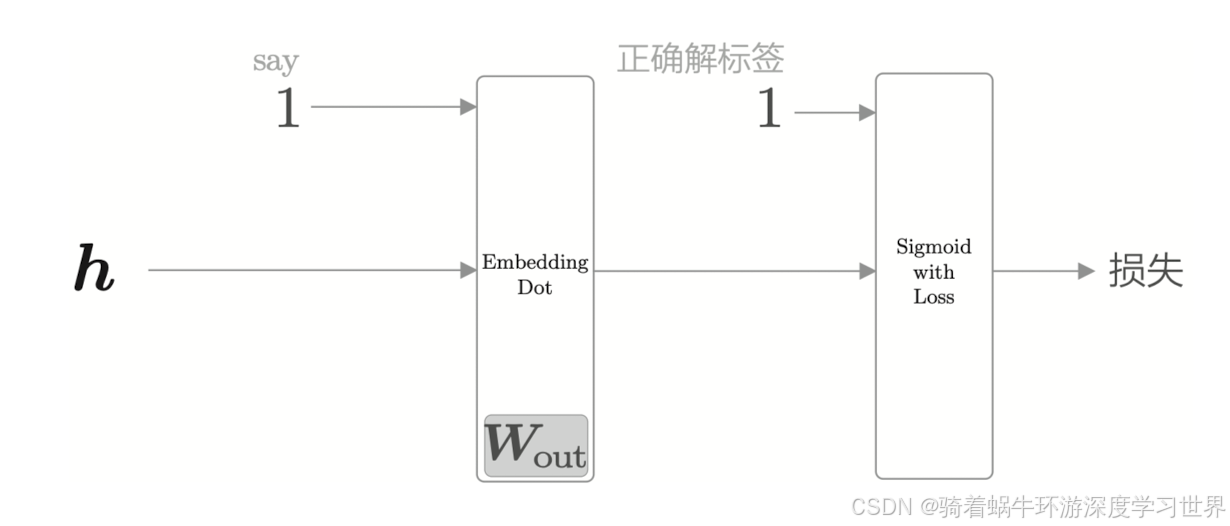
  1. 之前我们实现的神经网络是为了回答：当上下文是 you 和 goodbye 时，目标词是什么”这个问题；如果转换为二分类问题，则需要神经网络回答的是：当上下文是 you 和 goodbye 时，目标词是say吗”这个问题

  2. 按照3问题分析二最后说的那样，取权重矩阵 w o u t w_{out} wout​​中单词say对应的那一列（维度为[100,1]）与中间层结果（维度为[1,100]）计算内积，得到一个标量，如下图所示；对于一个标量，是无法计算softmax的，而是需要使用sigmoid函数转换为概率，然后计算损失。

在这里插入图片描述

4.1.1概率转换与损失计算

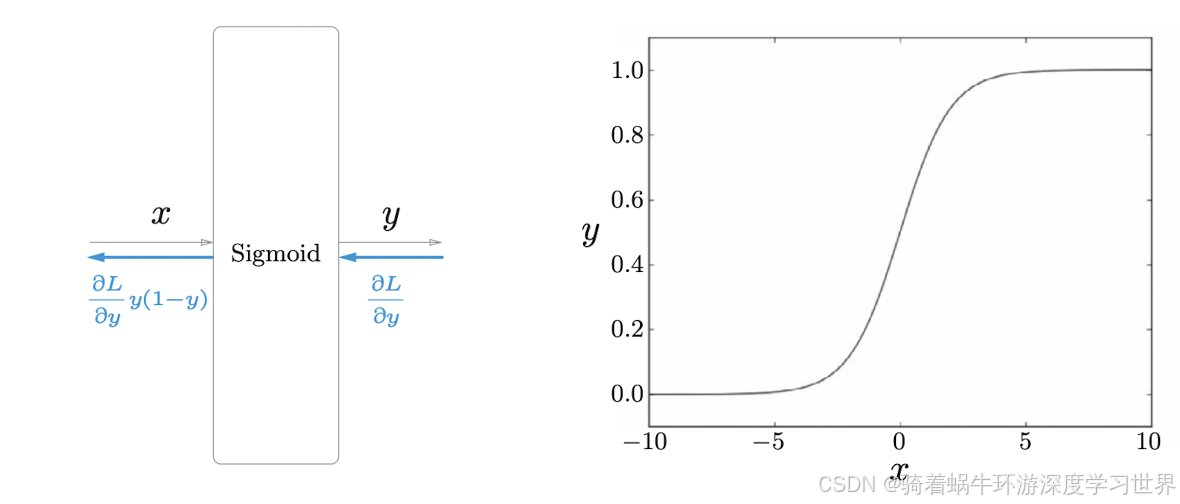
  1. sigmoid函数如下所示；该函数能够将输入的标量转化为0到1之间的数；这个结果可以被解释为概率；
    y = 1 1 + exp ⁡ ( − x ) y=\frac1{1+\exp(-x)} y=1+exp(−x)1​
    在这里插入图片描述

  2. 接下来就和之前一样，根据计算出的概率，结合真实的标签，计算交叉熵损失；

  3. 交叉熵损失简单说就是真实标签乘上对应的概率值；由于这里处理的是二分类问题（本质上与之前多分类时提到的交叉熵公式是一样的），因此标签的取值非0即1；

  4. 因此二分类的交叉熵损失函数可以用下式表示：
    L = − ( t log ⁡ y + ( 1 − t ) log ⁡ ( 1 − y ) ) L=-(t\log{y}+(1{-}t)\log{(1{-}y)}) L=−(tlogy+(1−t)log(1−y))
    其中 t = 0 t=0 t=0或者 t = 1 t=1 t=1； t t t表示真实标签。

4.1.2反向传播

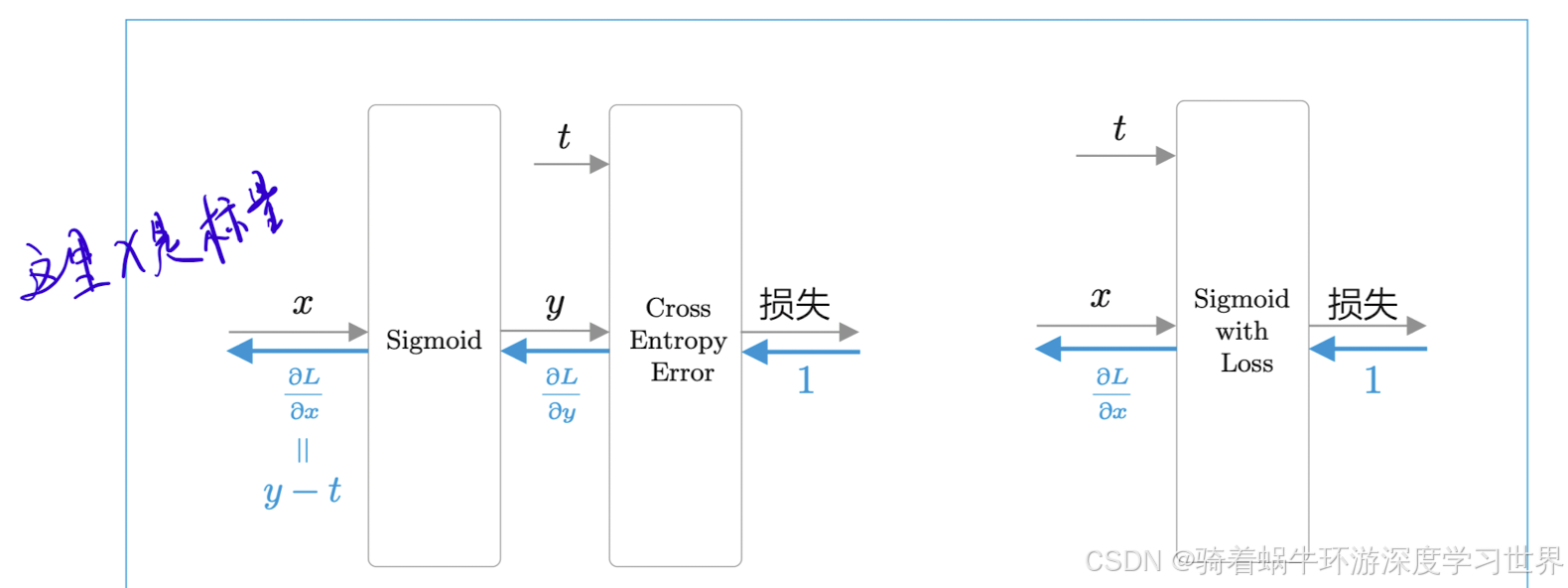
  1. 中间层输出会进入sigmoid层以及交叉熵损失层，结构图如下图所示：

    在这里插入图片描述

  2. 这两个层的反向传播计算过程见这个视频：11-二分类问题中sigmoid函数和交叉熵损失的反向传播计算过程_哔哩哔哩_bilibili；

    1. 注意：当前是选择了输出侧权重矩阵中单词say对应的那一列的列向量，与中间层输出做内积；因此输入到sigmoid层的是一个标量；
    2. 看完反向传播计算过程，我们就可以知道，对于输入的标量x，该处的梯度是y-t；y表示x经过sigmoid层的输出，t是真实标签，取值为0或者1，即回答了”当前待预测目标词是不是say“；
    3. 可以发现，前面Softmax函数和交叉熵误差的组合在反向传播时也是y-t。

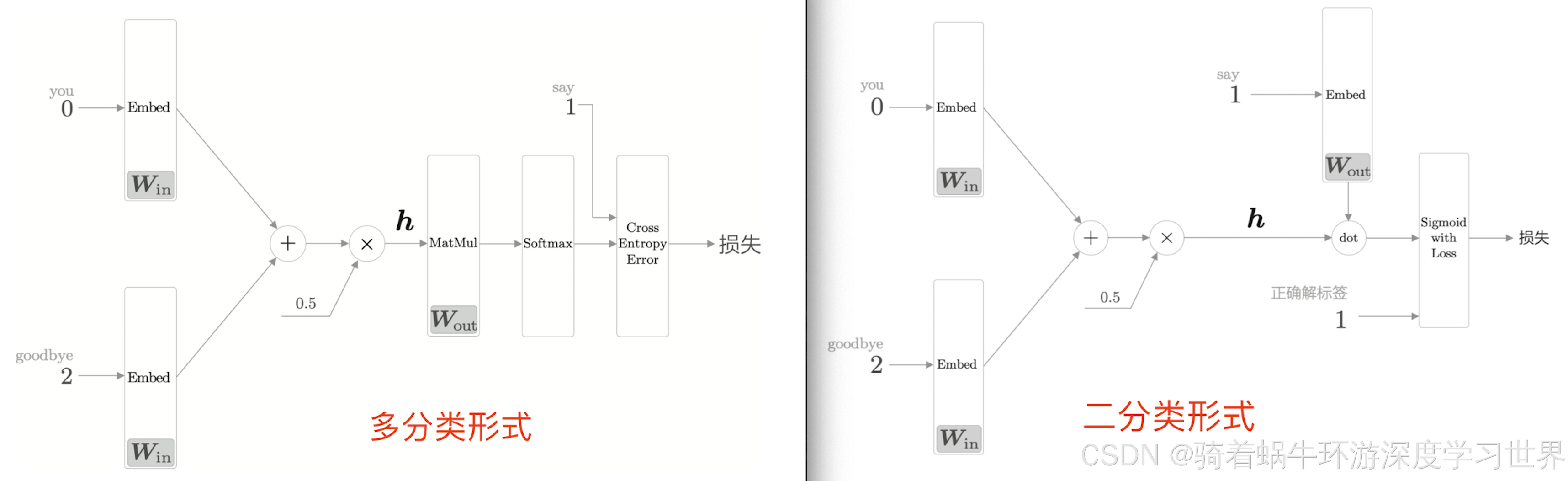
4.1.3多分类与二分类的网络结构的对比

这里我们再来对比一下之前的多分类的形式与现在二分类形式的区别（前提是我们目前只看预测say这一个目标词）

  1. 下图为两种网络结构的对比：

    1. 多分类情况下输出侧神经元个数为语料库单词数，然后使用softmax函数将得分概率化，然后选择最大的作为预测值；
    2. 二分类情况下输出侧神经元只有一个，即say那一列对应的列向量与中间层结果的内积结果；然后使用sigmoid函数转换为概率，并根据设定的阈值决定预测为yes还是no；
    3. say的单词ID是1，在二分类时被用于从权重矩阵中选择特定的列；
    4. 二分类情况下正确解标签可能是1也可能是0；因为这里目标词是say，而我们从权重矩阵中选取的列就是say那一列，因此正确解标签就是1；
    5. 注意：这里两种情况下输入侧的结构都换成了前面说的Embedding层了；

    在这里插入图片描述

4.1.4 Embedding Dot层

代码位置：utils\Embedding.py；

  1. 上图中，二分类形式下，从 W o u t W_{out} Wout​中取出特定列的过程也可以称之为Embedding层（正如图中用Embed来标记的那样），只不过与输入侧正好相反，输入侧是从权重矩阵 W i n W_{in} Win​中取出特定行；

  2. 本书中将输出侧的这个Embedding层和内积计算合并成一个层来简化模型结构图；简化之后的结构图如下图所示：

    在这里插入图片描述

  3. Embedding Dot层的初始化和前向传播代码如下所示：

    1. Embedding_dot层的参数就是Embedding层的参数，即原本输出侧的权重矩阵 W o u t W_{out} Wout​；不过按照这里的实现过程，初始化Embedding_dot层时传入的W需要先转置一下；
    2. idx是一个列表，里面是要取出来的单词对应的ID；目前还是取每一条数据对应的正确解标签的那个列向量；由于W已经转置，target_w是[batch_size,100]，与h的维度一样；
    3. 通过target_w*h计算对应元素的乘积，结果的维度保持不变，依然是[batch_size,100]；然后在第二个维度上求和，即每条数据的内积结果，是一个值；多条数据的结果组织在一起，则out的维度是[batch_size,1]；
    class Embedding_dot:
    def __init__(self, W):
        self.embed=Embedding(W) # 直接用上面构建好的embedding层
        self.params=self.embed.params # Embedding_dot层的参数就是Embedding层的参数
        self.grads=self.embed.grads # Embedding_dot层的梯度就是Embedding层的梯度
        self.cache=None # 缓存，用于存放前向计算的结果，反向传播时需要用

    def forward(self,h,idx):
        '''
        @param h: 中间层的结果，形状为(1,hidden_dim);如[1,100]
        @param idx: 要进行二分类的那个正确解标签对应的ID；比如say对应的ID'''
        target_w=self.embed.forward(idx) # 这里会获取w的行，因此初始化时传入的输出测权重需要转置一下;target_w维度为[1,100]
        out=np.sum(target_w*h,axis=1) # 对应元素相乘再相加;如果一次处理好几条数据，则out的维度是[batch_size,]
        self.cache=(h,target_w) # 反向传播时需要用到这两个量

        return out

  4. 下图是书上的一个具体数据的示意图：

    1. 像上面说的，权重矩阵 W o u t W_{out} Wout​本来维度是[hidden_dim,vocab_size]，按照二分类的做法，是取一列 w o u t w_{out} wout​（维度为[hidden_dim,1]）与中间层结果h（维度为[1,hidden_dim]）相乘： h ∗ w o u t = ( 1 , h i d d e n _ d i m ) ∗ ( h i d d e n _ d i m , 1 ) = ( 1 , 1 ) h*w_{out}=(1,hidden\_dim)*(hidden\_dim,1)=(1,1) h∗wout​=(1,hidden_dim)∗(hidden_dim,1)=(1,1)；
    2. 这里为了复用前面的Embedding层，对权重矩阵 W o u t W_{out} Wout​进行转置；所以取出来的每个 w o u t w_{out} wout​维度就是[1,hidden_dim]，与h维度相同了；正好可以用*乘计算对应元素的乘积，然后用np.sum求和；

    在这里插入图片描述

  5. 接下来是反向传播的代码实现；我们考虑mini-batch的情况：

    def backward(self,dout):
    h,target_w=self.cache
    dout=dout.reshape(dout.shape[0],1) # 这里是为了保证dout的形状与h的形状一致
    dtarget_w=dout*h # 对应元素相乘;dout:[batch_size,1];h:[batch_size,hid_dim];所以会进行广播;
    self.embed.backward(dtarget_w) # 把梯度更新到权重矩阵的梯度矩阵的对应行；先前在执行self.embed.forward(idx)时已经保存了使用的idx
    dh=dout*target_w # 对应元素相乘;会进行广播;
    return dh
    1. 由上图可知，np.sum求和之后out的维度会比 h ∗ w o u t h*w_{out} h∗wout​少一个，即维度数为1；但是反向传播时out的梯度需要与Embedding Dot层的局部梯度相乘，而局部梯度都是两个维度，所以需要给dout增加一个维度；
    2. 反向传播时，需要分别计算对权重矩阵 W o u t W_{out} Wout​和输入h的梯度；对应的前向传播是内积，即 o u t = h 1 w 1 + h 2 w 2 + . . . out=h_1w_1+h_2w_2+... out=h1​w1​+h2​w2​+...；
      1. 对每个 w w w求偏导，局部梯度就是对应的 h h h；
      2. 对每个 h h h求偏导，局部梯度就是对应的 w w w；
      3. 由此可见，反向传播时需要用到前向计算时的结果，即self.cache=(h,target_w)；

4.2负采样

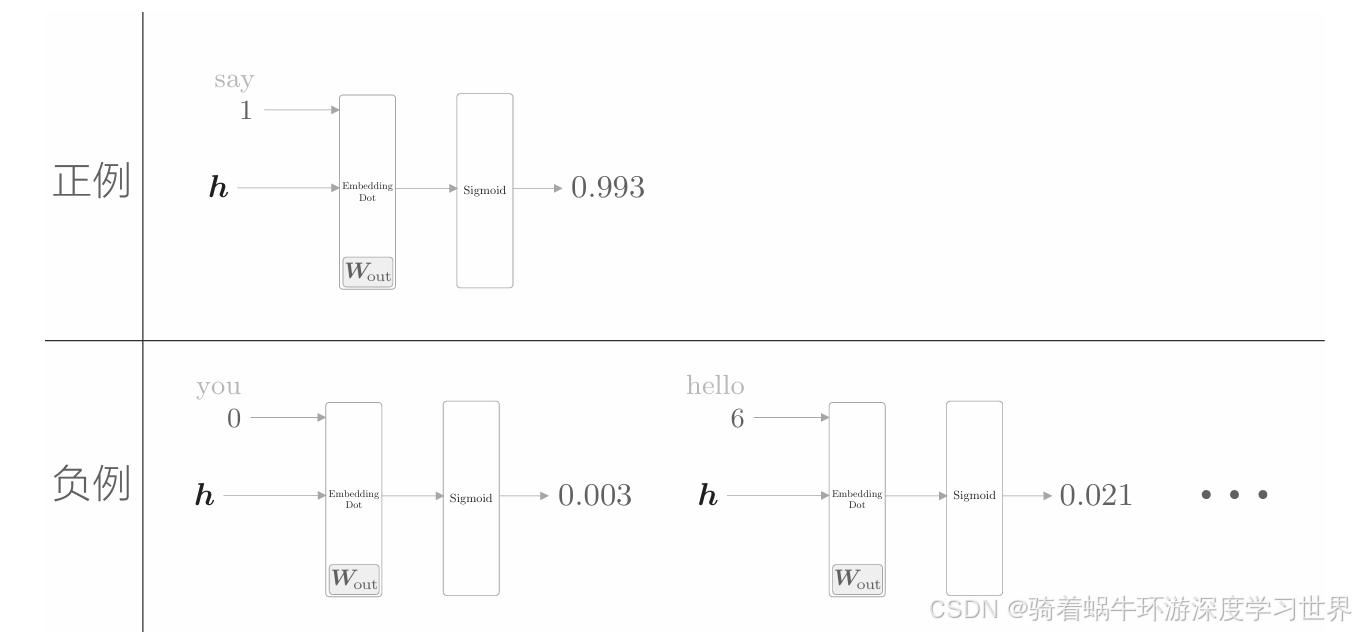
  1. 为了把多分类问题处理为二分类问题，对于“正确答案”（正例）和“错误答案”（负例），都需要能够正确地进行分类（二分类）。因此，需要同时考虑正例和负例。

  2. 目前我们只是从输出侧权重矩阵中选择了正确解标签对应的向量，让模型预测；即仅仅让模型学习正确答案，还没有学习错误答案（负例）；

  3. 换句话说，通过上面的过程，模型能够对正确解标签输出尽可能高的概率；但我们还需要让模型对错误答案标签输出尽可能低的概率；如下图所示：

    在这里插入图片描述

  1. 本身这里就是要解决前面softmax等操作在语料库很大时的计算问题，因此这里负采样肯定不能对所有的负例都进行学习；否则改进就失去了意义；

  2. 因此，负采样将选择若干个负例，对这些负例求损失。然后，将这些数据（正例 和采样出来的负例）的损失加起来，将其结果作为最终的损失。

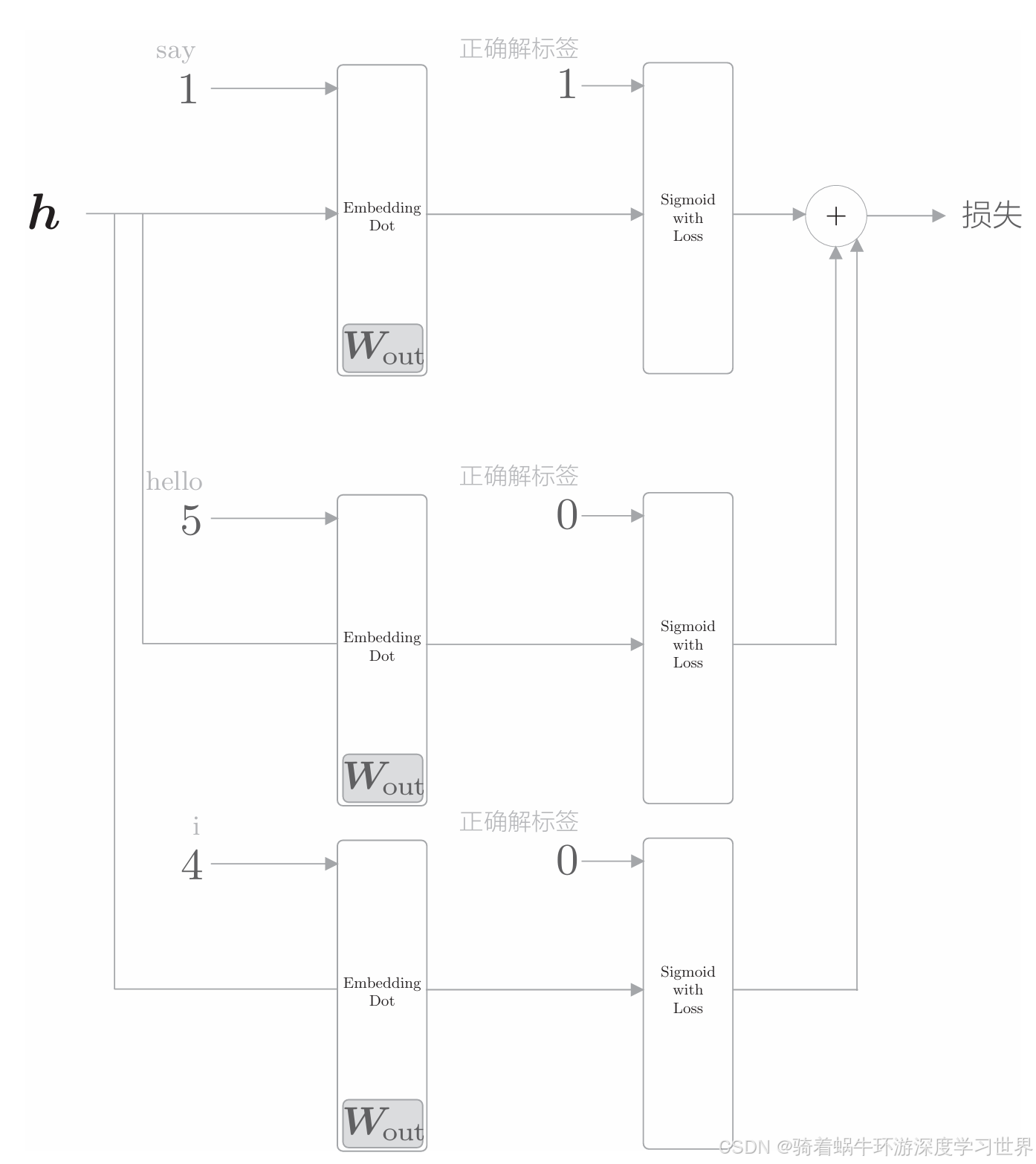
  3. 下图为负采样个数为2的局部计算图，即负采样了单词hello和i：

    1. 由于单词hello和i是负例，即错误答案，因此正确解标签应该是0；
    2. 正例与负例的损失最后求和作为最终损失。

    在这里插入图片描述

4.2.1负采样方法

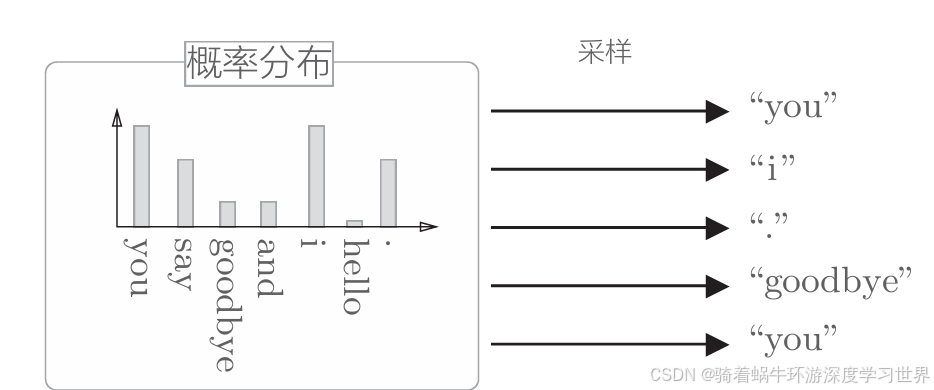
  1. 如何抽取负例：让语料库中经常出现的单词容易被抽到，让语料库中不经常出现的单词难以被抽到；原因如下：

    1. 由于负采样是抽样，因此每次不会覆盖所有的负例；但是我们又希望模型能够尽可能的覆盖负例单词；
    2. 那么如果我们多抽取那些经常出现的单词，相当于覆盖范围就广了；
    3. 出现频率低的单词，模型较少学习，对整体效果的影响也不大。

  2. 具体而言：先计算语料库中各个单词的出现次数，并将其表示为“概率分布”，然后使用这个概率分布对单词进行采样；如下图所示：

    在这里插入图片描述

  3. 代码层面，需要使用np.random.choice()方法；书上的几个示例如下图所示：

    在这里插入图片描述

    1. 通过size参数执行多次采样；通过replace=False参数执行无放回采样；通过参数p执行根据概率采样；

    2. 这三个参数可以进行组合；下图是一个例子；

      在这里插入图片描述

  4. 负采样概率的微调：word2vec中提出的负采样对刚才的概率分布增加了一个步骤，对原来的概率分布取0.75次方，之后再执行负采样；如下式所示：
    P ′ ( w i ) = P ( w i ) 0.75 ∑ j P ( w j ) 0.75 P'(w_i)=\frac{P(w_i)^{0.75}}{\sum_jP(w_j)^{0.75}} P′(wi​)=∑j​P(wj​)0.75P(wi​)0.75​

    1. 首先0.75次方这个具体的值是根据实验得出的，也可以设置成其他的值；其次，取了次方之后，概率之和就不为1了，所以做了归一化；

    2. 最后，这样做的目的是：为了防止低频单词被忽略，取了次方可以让概率大的没那么大，概率小的没那么小；如下图所示：

      在这里插入图片描述

4.2.1.1负采样的代码实现

utils\negativeSamplingLayer.py；

  1. 初始化：主要是计算每个单词在语料库中出现的次数；代码如下：

    class UnigramSampler:
    def __init__(self, corpus, power, sample_size):
        self.sample_size = sample_size
        self.vocab_size = None
        self.word_p = None

        counts = collections.Counter()
        for word_id in corpus:
            # 统计每个单词出现的次数
            counts[word_id] += 1

        vocab_size = len(counts)
        self.vocab_size = vocab_size

        self.word_p = np.zeros(vocab_size) # 存放每个单词出现的概率
        for i in range(vocab_size):
            self.word_p[i] = counts[i]

        self.word_p = np.power(self.word_p, power)
        self.word_p /= np.sum(self.word_p)

    1. self.word_p的计算进行了变通，本质上和先求概率、然后加次方、最后归一化是一样的；下图是一个简单的证明：

      在这里插入图片描述

      1. 其中 t i t_i ti​表示单词 i i i出现的次数； p i p_i pi​表示单词 i i i出现的概率；上标 e e e表示取次方；

  2. 进行负采样的代码如下：就是将上面np.random.choice()方法在这里进行使用；

    def get_negative_sample(self, target):
    '''
    @param target: 正确解标签;维度为(batch_size,)'''
    batch_size = target.shape[0]

    negative_sample = np.zeros((batch_size, self.sample_size), dtype=np.int32)

    for i in range(batch_size):
        p = self.word_p.copy()
        target_idx = target[i]
        p[target_idx] = 0 # 将正确解标签的概率设置为0，则不会抽到它了
        p /= p.sum() # 因为修改了p所以要重新归一化
        negative_sample[i, :] = np.random.choice(self.vocab_size, size=self.sample_size, replace=False, p=p)

    return negative_sample
    1. 直接使用self.vocab_size作为采样范围是因为传入的p中概率值的排列顺序与corpus中单词的排列顺序一致；

  3. 运行如下的示例：

    if __name__ == "__main__":
    corpus = np.array([0, 1, 2, 3, 4, 1, 2, 3])  # (8,)
    power = 0.75
    sample_size = 2

    sampler = UnigramSampler(corpus, power, sample_size)  # sampler.word_p:(5,)
    target = np.array([1, 3, 0])  # (3,)
    negative_sample = sampler.get_negative_sample(target)  # (3, 2)
    print(negative_sample)  # [[2 3],[0 2],[1 2]]

5整合

将输出侧的二分类改进与负采样方法整合到一起，构建negative_sampling_layer层，这里我们可以认为是整个输出层；

  1. 层的初始化，包括初始化负例采样器、正例与负例都要用的Embedding Dot层以及损失计算层

5.1损失计算层SigmoidWithLoss的实现

代码位于：utils\SigmoidWithLoss.py；

  1. 由于换成了sigmoid函数，因此损失计算的实现也需要进行修改；

    1. 初始化：损失函数只是进行计算，不存在参数，只需要传递梯度；为了统一，也设置了参数和梯度的成员变量。

      class SigmoidWithLoss:
    def __init__(self):
        self.params, self.grads = [], []
        self.loss = None
        # 用于前向计算时保存y和t,反向传播时需要用到
        self.y = None  # sigmoid的输出
        self.t = None  # 监督标签

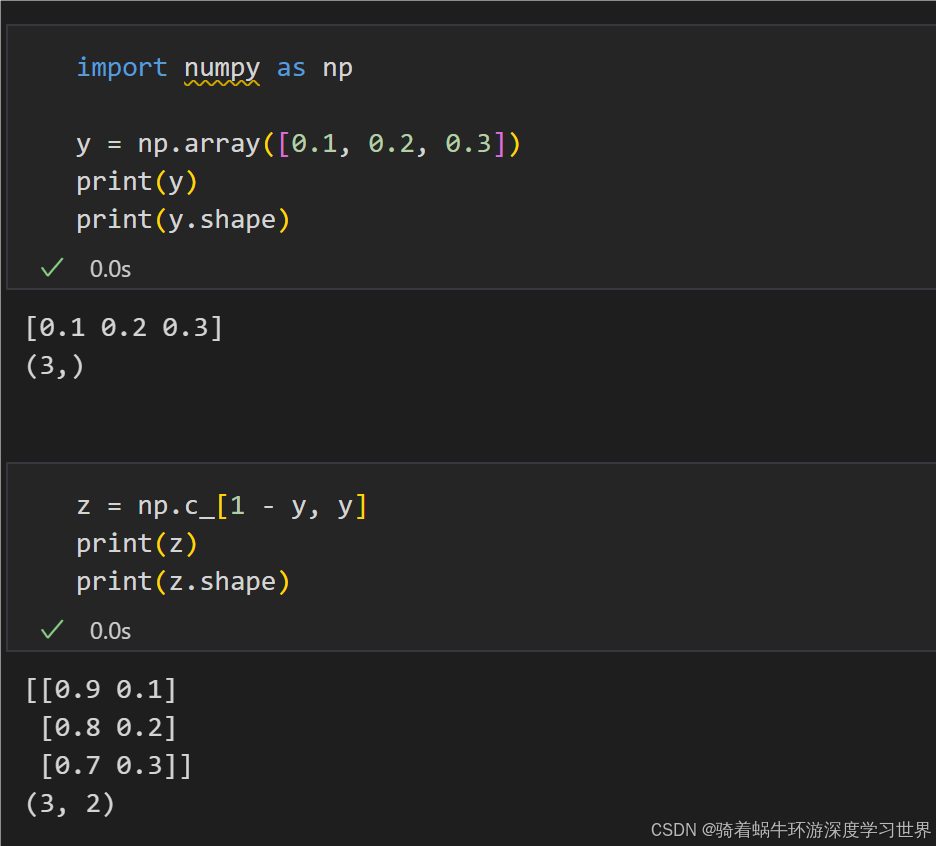
    2. 前向计算：首先对输入的x计算sigmoid函数值，转换为概率得分；然后与真实标签一起输入到cross_entropy_error中计算损失：

      def forward(self, x, t):
    '''
    @param x: sigmoid的输入;维度为[batch_size,]
    @param t: 监督标签;维度为[batch_size,]'''

    self.t = t
    self.y = 1 / (1 + np.exp(-x)) # 不管是标量还是向量，sigmoid函数都是作用在其中的每个元素上

    # np.c_[1 - self.y, self.y]之后维度变成[batch_size,2]
    self.loss = cross_entropy_error(np.c_[1 - self.y, self.y], self.t)

    return self.loss

      1. 这里复用了之前的cross_entropy_error；

      2. self.y、1 - self.y的维度为[batch_size,]；np.c_[1 - self.y, self.y]将这两个一维向量按列拼接，拼接后维度为[batch_size,2]，下图是一个示例：

        在这里插入图片描述

      3. 之后进入cross_entropy_error函数中，两个判断都不执行，直接计算交叉熵损失；通过np.arange(batch_size)和一维向量t，从np.c_[1 - self.y, self.y]中，每行抽取一个概率值（ t = 1 t=1 t=1则抽取的是正确解标签1对应的概率， t = 0 t=0 t=0则抽取的是正确解标签0对应的概率）；另外，由于损失函数中一项是t，一项是1-t，所以 t = 1 t=1 t=1则另一项就是0，不用考虑，因此只需要抽取当前输入的t对应的概率值即可；

        在这里插入图片描述

      4. 为什么都变成二分类了，还可以共用一个cross_entropy_error函数：二分类这里y的维度为[batch_size,2]，t是0或者1；之前多分类时y的维度为[batch_size,vocab_size]，t是正确解标签，即单词ID值；都是要选择t对应的概率值计算损失，二分类时的两个类别本质上和多分类时的词范围是一样的。

    3. 反向传播

      1. 前面通过推导得出梯度是y-t的结论，所以这里反向传播就很简单了；
      def backward(self, dout=1):
    '''本质上是对sigmoid函数的输入求梯度'''
    batch_size = self.t.shape[0]

    dx = (self.y - self.t) * dout / batch_size # 这里将梯度平均了
    return dx

5.2输出层negative_sampling_layer的实现

代码位于：utils\negativeSamplingLayer.py；

  1. 初始化代码如下：

    1. 我们假设列表的第一个层处理正例。也就是说，loss_layers[0]和embed_dot_layers[0]是处理正例的层；
    class NegativeSamplingLoss:
    def __init__(self, W, corpus, power=0.75, sample_size=5):
        self.sample_size = sample_size
        self.sampler = UnigramSampler(corpus, power, sample_size) # 负例采样器
        # 每个正例和负例都有一个EmbeddingDot层和一个SigmoidWithLoss层
        self.loss_layers = [SigmoidWithLoss() for _ in range(sample_size + 1)]
        self.embed_dot_layers = [EmbeddingDot(W) for _ in range(sample_size + 1)]

        self.params, self.grads = [], []
        # 输出侧参数只存在于EmbeddingDot层
        for layer in self.embed_dot_layers:
            self.params += layer.params
            self.grads += layer.grads

  2. 前向计算代码如下：

    1. 先根据输入的正确解标签采样负例，然后分别对正例和负例进行前向计算，并累加损失值；
    def forward(self, h, target):
    '''
    @param h: 中间层的结果，维度为(batch_size,hidden_dim)
    @param target: 正确解标签;维度为(batch_size,)'''

    batch_size = target.shape[0]
    # 获取self.sample_size个负例解标签
    negative_sample = self.sampler.get_negative_sample(target) # (batch_size,sample_size)

    # 正例的正向传播
    score = self.embed_dot_layers[0].forward(h, target) # (batch_size,)
    correct_label = np.ones(batch_size, dtype=np.int32) # (batch_size,)
    loss = self.loss_layers[0].forward(score, correct_label)

    # 负例的正向传播
    negative_label = np.zeros(batch_size, dtype=np.int32) # (batch_size,)
    for i in range(self.sample_size):
        # 对每一个负例样本，依次计算损失并累加到正例的损失上去
        negative_target = negative_sample[:, i] # (batch_size,)
        score = self.embed_dot_layers[1 + i].forward(h, negative_target) # (batch_size,)
        loss += self.loss_layers[1 + i].forward(score, negative_label)

    return loss

  3. 反向传播代码如下：

    1. negative_sampling_layer的输入是中间层的结果h，因此需要返回h的梯度；
    2. 代码中依次对正例和每个负例所在的网络结构进行反向传播；
    def backward(self, dout=1):
    dh = 0
    # 中间层结果h到输出侧是进入了多个分支，因此反向传播时梯度需要累加
    for l0, l1 in zip(self.loss_layers, self.embed_dot_layers):
        # 依次对正例和每个负例所在的网络结构进行反向传播
        dscore = l0.backward(dout) # 损失函数(sigmoid和交叉熵损失)的反向传播,即y-t的结果
        dh += l1.backward(dscore) # Embedding_dot的反向传播，包含保存各自权重矩阵对应的行的梯度

    return dh

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
模拟退火算法4—应用
sklearn 命令行安装_sklearn 安装说明
推荐10 款 C++ 在线编译器
Vue3项目集成CKEditor富文本编辑器，支持代码语法高亮显示
JS PC端调用摄像头录视频截图上传文件
求解固定长度的回文子序列数目
Mybatis逆向工程（idea）
青龙面板 依赖一键安装
Vue3 混入
KVM虚拟机无法启动
;