3.4-GRU - 悦读

1网络结构

1.1与LSTM相比

LSTM里面有三个门，还有一个增加信息的tanh单元，参数量相较于RNN显著增加；
因此GRU在参数上比LSTM要少；
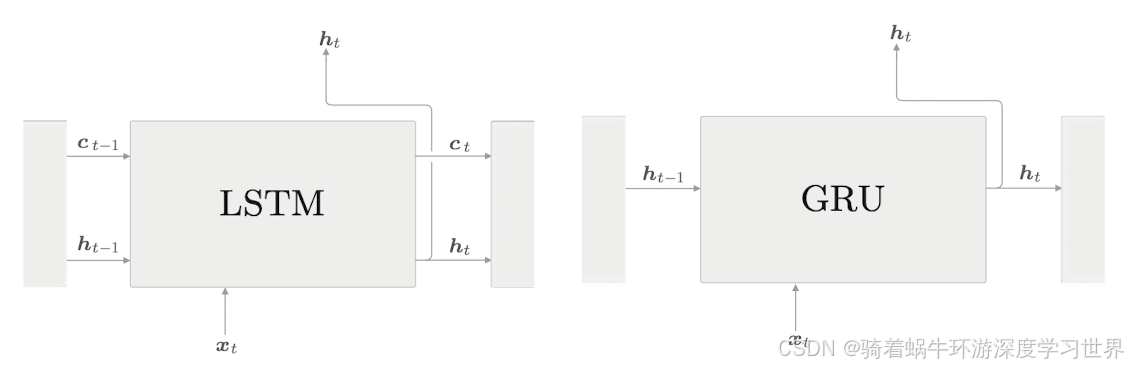
另外，LSTM 将必要信息记录在记忆单元中，并基于记忆单元的信息计算隐藏状态。与此相对，GRU 中不需要记忆单元这样的额外存储；如下图所示：

1.2 GRU具体的网络结构

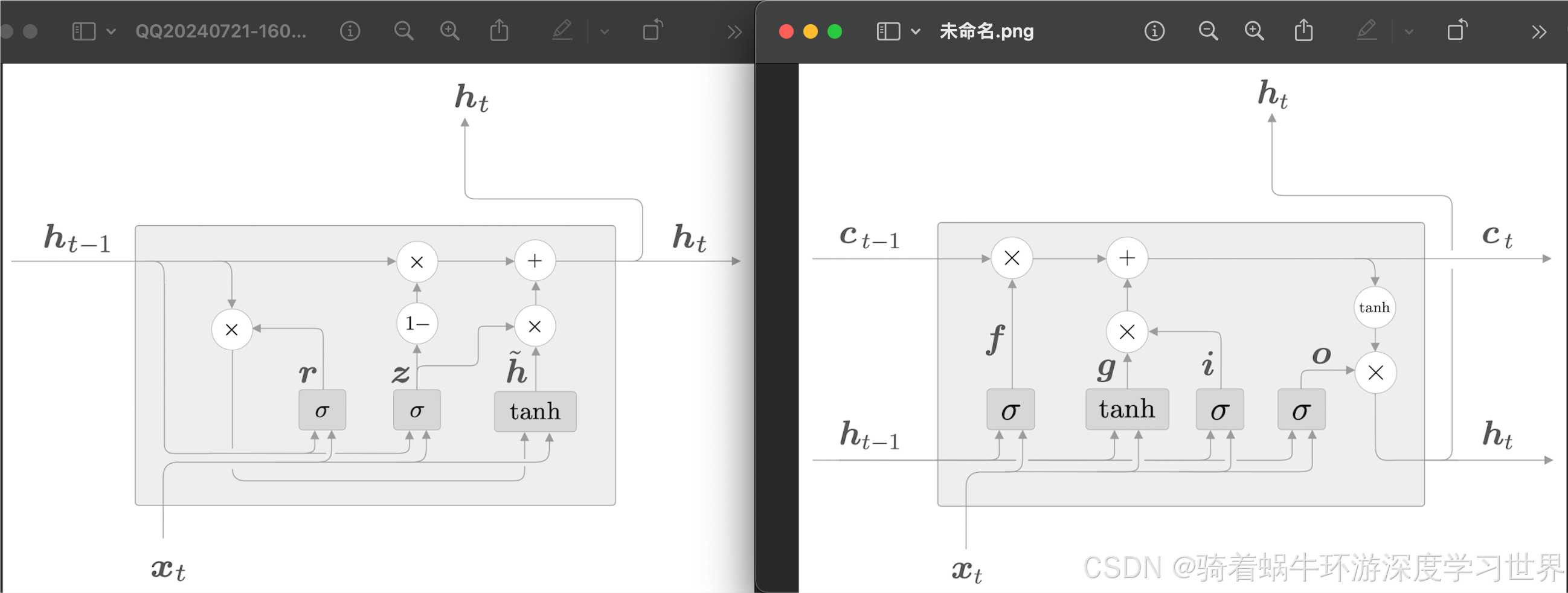
GRU的结构如下图；右边是LSTM的结构图，作为对比：
1. LSTM能够控制梯度的流动就是因为记忆单元那条梯度流动的路径上只有加法和对应元素相乘的乘法；
2. GRU这里虽然去掉了额外的记忆单元，但是隐藏信息是也是从加法和对应元素相乘的乘法路径上流过的，因此梯度消失问题也可以得到缓解；
GRU的计算涉及以下公式：
$\boldsymbol{z}=\sigma(\boldsymbol{x}_{t}W_{x}^{{(\mathrm{z})}}+\boldsymbol{h}_{t-1}W_{h}^{{(\mathrm{z})}}+\boldsymbol{b}^{{(\mathrm{z})}}) \tag{1}$

$\boldsymbol{r}=\sigma(\boldsymbol{x}_{t}W_{x}^{{(\mathrm{r})}}+\boldsymbol{h}_{t-1}\boldsymbol{W}_{h}^{{(\mathrm{r})}}+\boldsymbol{b}^{{(\mathrm{r})}}) \tag{2}$

$\tilde{\boldsymbol{h}}=\tanh(\boldsymbol{x}_t\boldsymbol{W}_x+(\boldsymbol{r}\odot\boldsymbol{h}_{t-1})\boldsymbol{W}_h+\boldsymbol{b}) \tag{3}$

$\boldsymbol{h}_t=(1-\boldsymbol{z})\odot\boldsymbol{h}_{t-1}+\boldsymbol{z}\odot\tilde{\boldsymbol{h}} \tag{4}$
由于GRU的输出只有 $\boldsymbol{h}_t$ ，因此需要结合两个部分的信息：旧的信息 $(1-\boldsymbol{z})\odot\boldsymbol{h}_{t-1}$ 和新的信息 $\boldsymbol{z}\odot\tilde{\boldsymbol{h}}$ ；不像LSTM专门有一个记忆单元，旧的和新的记忆都被先存到了记忆单元里面，所以LSTM的隐藏状态直接基于当前时刻的记忆单元；所以类比LSTM的门结构，有以下说明：
1. $\boldsymbol{z}\odot\tilde{\boldsymbol{h}}$ 是新的信息，所以 $\boldsymbol{z}$ 相当于输入门，对新增信息进行加权；
2. $(1-\boldsymbol{z})\odot\boldsymbol{h}_{t-1}$ 是旧的信息，所以 $(1-\boldsymbol{z})$ 充当了遗忘门，给上一个隐藏状态加权，决定哪些信息的权重可以降低；
3. 因此， $\boldsymbol{z}$ 这里的门结构称为更新门，同时充当了输入门和遗忘门的作用；
还有一个重置（reset）门 $\boldsymbol{r}$ ，决定在多大程度上“忽略”过去的隐藏状态；
1. 如果 $\boldsymbol{r}$ 是0，则根据(3)式和(4)式，新的隐藏状态 $\boldsymbol{h}_t$ 仅取决于当前时刻的输入 $\boldsymbol{x}_t$ ；

1.3 LSTM和GRU选哪个

不是绝对的；根据不同的任务和超参数设置，结论可能不同；
因为 GRU 的超参数少、计算量小，所以特别适合用于数据集较小、设计模型需要反复实验的场景。

2 GRU的代码实现

所有代码位于：GY/basicNLP (gitee.com)；

代码位于：GRU_model/GRU.py；

2.1初始化

与LSTM相比，GRU少了一个门，但是参数还是整合在一起；因此维度从4H变成3H；代码如下：

class GRU:
    def __init__(self, Wx, Wh, b):
        '''输入参数都是整合了四个仿射变换的参数
        @param Wx: (D, 3H)
        @param Wh: (H, 3H)
        @param b: (1, 3H)'''
        self.params = [Wx, Wh, b]
        if GPU:
            self.grads = [to_gpu(np.zeros_like(Wx)), to_gpu(np.zeros_like(Wh)), to_gpu(np.zeros_like(b))]
        else:
            self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
        self.cache = None

2.2前向计算

LSTM的几个门的计算，都是使用 $\boldsymbol{x}_{t}$ 和 $\boldsymbol{h}_{t-1}$ ；因此可以先把四个参数整合到一起先统一算矩阵乘法；而GRU这里只有式子(1)(2)是可以整合的；所以这里在实现的时候单纯按照公式计算了；没有整合；

代码如下：

    def forward(self, x, h_prev):
        '''
        @param x: (N, D)
        @param h_prev: (N, H)
        @return h_next: (N, H)'''
        Wx, Wh, b = self.params
        H = Wh.shape[0]
        # 取出门以及tanh节点的权重以及偏置
        Wxz, Wxr, Wxh = Wx[:, :H], Wx[:, H:2 * H], Wx[:, 2 * H:]
        Whz, Whr, Whh = Wh[:, :H], Wh[:, H:2 * H], Wh[:, 2 * H:]
        bz, br, bh = b[:H], b[H:2 * H], b[2 * H:]
        # 直接按照公式计算
        z = sigmoid(np.dot(x, Wxz) + np.dot(h_prev, Whz) + bz) # z:(N,H);+bz时会进行广播
        r = sigmoid(np.dot(x, Wxr) + np.dot(h_prev, Whr) + br) # r:(N,H);
        h_hat = np.tanh(np.dot(x, Wxh) + np.dot(r * h_prev, Whh) + bh) #h_hat:(N,H)
        h_next = (1 - z) * h_prev + z * h_hat # *对应元素相乘

        self.cache = (x, h_prev, z, r, h_hat)

        return h_next

2.3反向传播

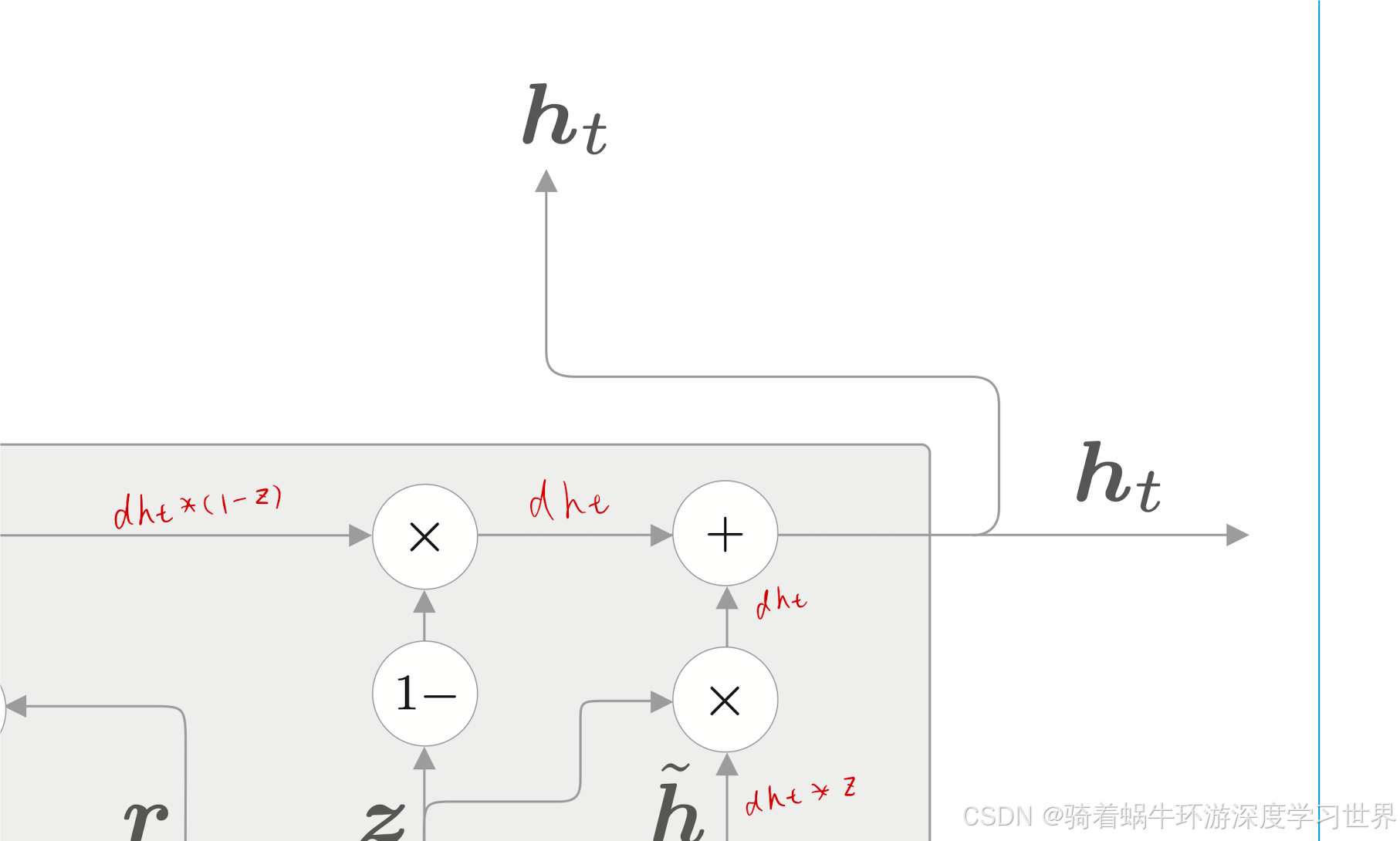
首先计算下图中红色字处的梯度：
1. 在代码上就体现为：
```
dh_hat =dh_next * z
dh_prev = dh_next * (1-z)
```
然后计算tanh节点的各个参数的梯度；根据下式；但此时是把 $\boldsymbol{r}\odot\boldsymbol{h}_{t-1}$ 看成数据；从结构图中也可以看出 $\boldsymbol{r}\odot\boldsymbol{h}_{t-1}$ 是与tanh节点分开的；
$\tilde{\boldsymbol{h}}=\tanh(\boldsymbol{x}_t\boldsymbol{W}_x+(\boldsymbol{r}\odot\boldsymbol{h}_{t-1})\boldsymbol{W}_h+\boldsymbol{b})$
1. 代码如下：
```
# tanh
dt = dh_hat * (1 - h_hat ** 2)
dbh = np.sum(dt, axis=0) # 广播;所以梯度累加回去
dWhh = np.dot((r * h_prev).T, dt)
dhr = np.dot(dt, Whh.T)
dWxh = np.dot(x.T, dt)
dx = np.dot(dt, Wxh.T)
```
然后就可以计算上一时刻隐藏状态的梯度了；它是两个分支梯度的和；
```
dh_prev += r * dhr
```

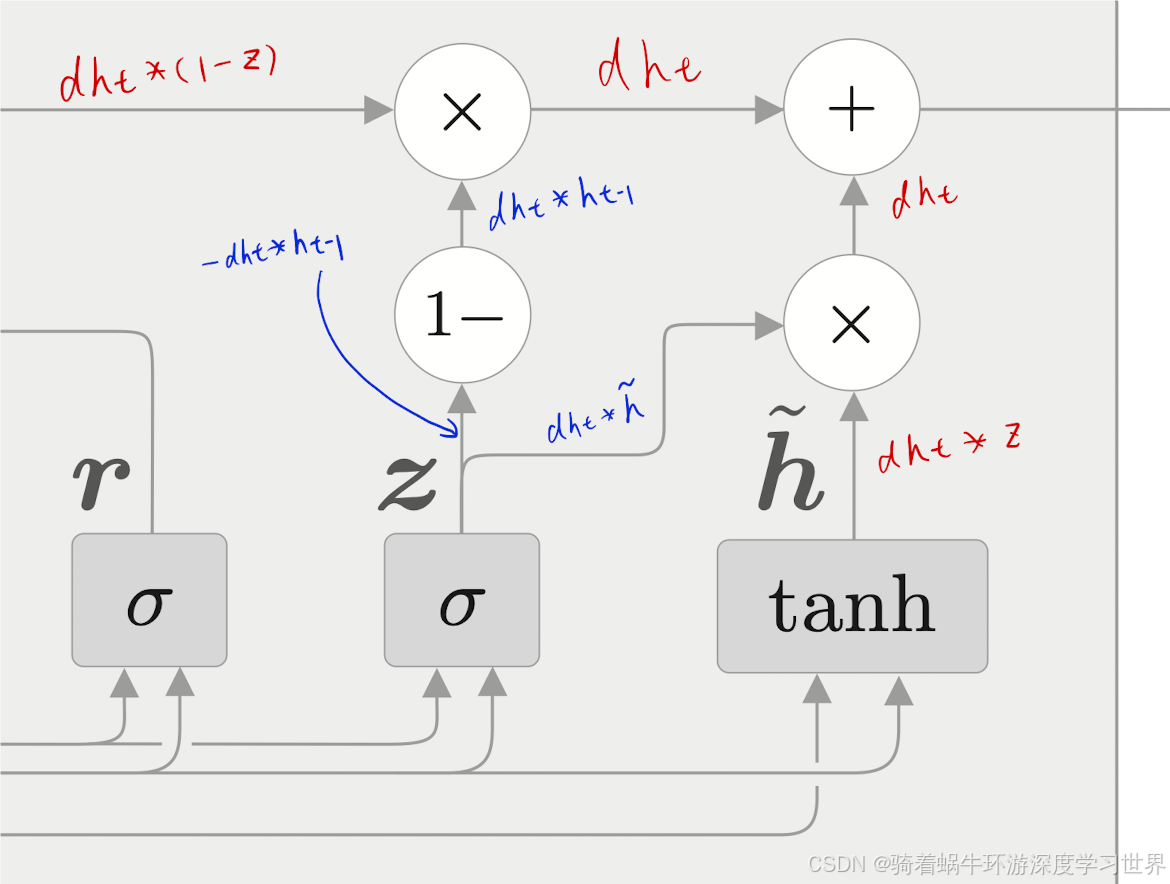
更新门 $\boldsymbol{z}$ 处的梯度如下图蓝色笔迹：

在这里插入图片描述

代码如下：

# update gate(z)
dz = dh_next * h_hat - dh_next * h_prev
dt = dz * z * (1-z) # 乘上sigmoid函数的局部梯度
# gate(z)这里仿射变换的梯度计算
dbz = np.sum(dt, axis=0) # 广播;所以梯度累加回去
dWhz = np.dot(h_prev.T, dt)
dh_prev += np.dot(dt, Whz.T)
dWxz = np.dot(x.T, dt)
dx += np.dot(dt, Wxz.T) # 与tanh节点处x的梯度累加

然后剩下一个重置门 $\boldsymbol{r}$ 的梯度计算；

# reset gate(r)
dr = dhr * h_prev
dt = dr * r * (1-r) # 乘上sigmoid函数的局部梯度
dbr = np.sum(dt, axis=0) # 广播;所以梯度累加回去
dWhr = np.dot(h_prev.T, dt)
dh_prev += np.dot(dt, Whr.T)
dWxr = np.dot(x.T, dt)
dx += np.dot(dt, Wxr.T)

整个梯度传播过程中，尤其注意输入 $\boldsymbol{x}_t$ 和上一时刻隐藏状态 $\boldsymbol{h}_{t-1}$ 梯度的累加；因为它们有好多分支；
最后对梯度进行整理；比如参数权重是整合在一起的，因此梯度也要整合一下；

3 Time GRU的代码实现

代码位于：GRU_model/GRU.py；

初始化：少了记忆单元；代码如下；

class TimeGRU:
    def __init__(self, Wx, Wh, b, stateful=False):
        self.params = [Wx, Wh, b]
        if GPU:
            self.grads = [to_gpu(np.zeros_like(Wx)), to_gpu(np.zeros_like(Wh)), to_gpu(np.zeros_like(b))]
        else:
            self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
        
        self.layers = None
        self.h, self.dh = None, None # 没有了记忆单元
        self.stateful = stateful

前向计算与Time LSTM相比，也是少了记忆单元；

    def forward(self, xs):
        '''
        @param xs: (N, T, D);N批数据;T时间步;D特征维度
        @return hs: (N, T, H)'''
        Wx, Wh, b = self.params
        N, T, D = xs.shape
        H = Wh.shape[0]
        self.layers = []
        if GPU:
            hs = to_gpu(np.empty((N, T, H), dtype='f'))
            if not self.stateful or self.h is None:
                self.h = to_gpu(np.zeros((N, H), dtype='f'))
        else:
            hs = np.empty((N, T, H), dtype='f')
            if not self.stateful or self.h is None:
                self.h = np.zeros((N, H), dtype='f')
                
        for t in range(T):
            layer = GRU(*self.params)
            self.h = layer.forward(xs[:, t, :], self.h)
            hs[:, t, :] = self.h
            self.layers.append(layer)
        return hs

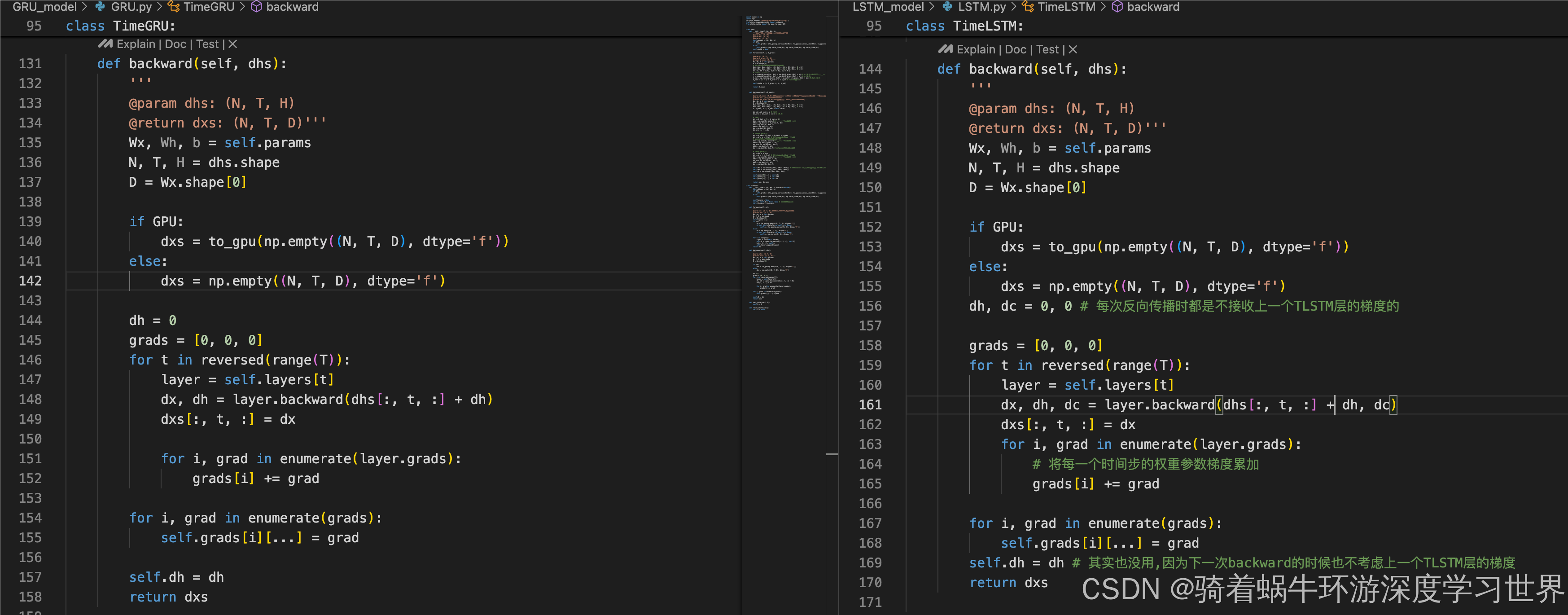
反向传播过程基本一致；

4基于PTB数据集对GRU模型进行训练和学习

4.1无改进的GRU训练和学习模型

代码位于：GRU_model/GRULM.py、GRU_model/train_GRULM.py；

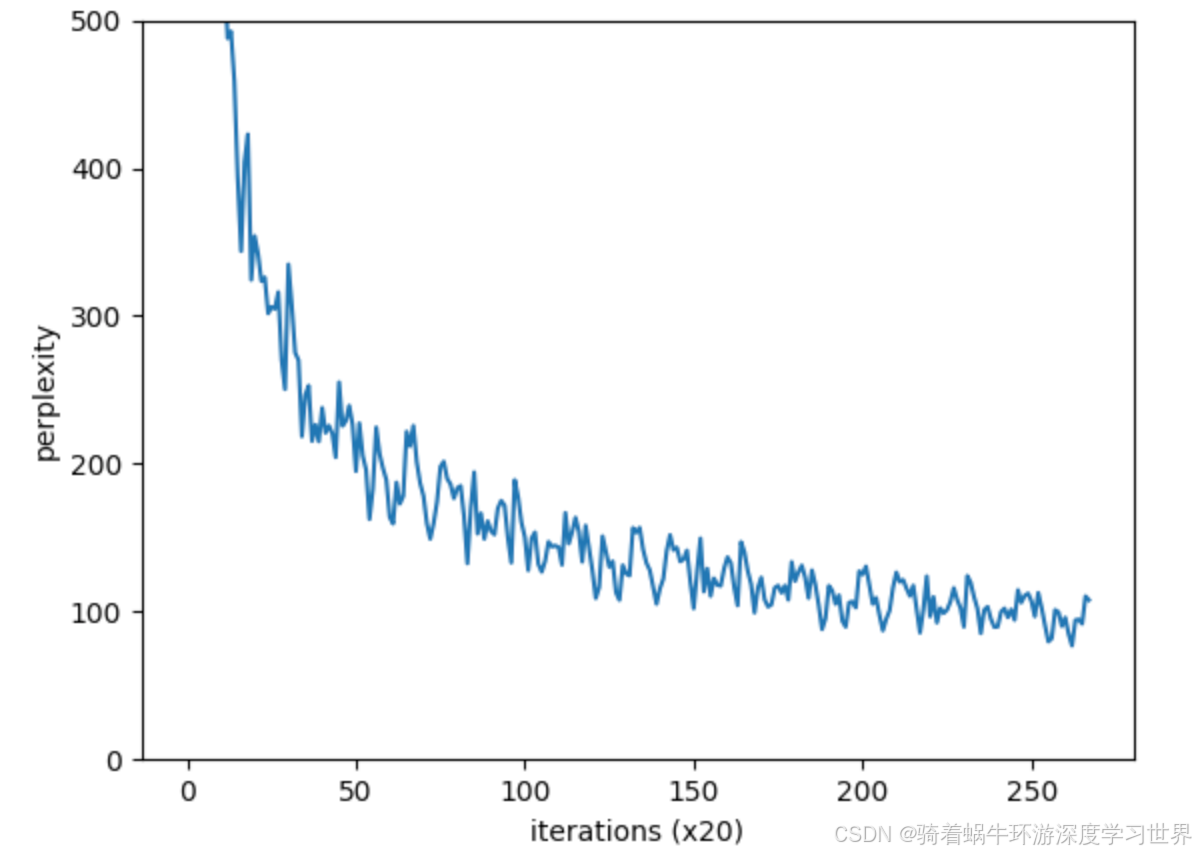
代码基本都一样；详见代码了；下图是训练过程中的困惑度曲线；跟LSTM的很相似；

4.2有改进的GRU训练和学习模型

代码位于：GRU_model/better_GRULM.py、GRU_model/train_better_GRULM.py；

这里的改进和LSTM那边一样，即权重共享、加入dropout层；然后GRU多层化；
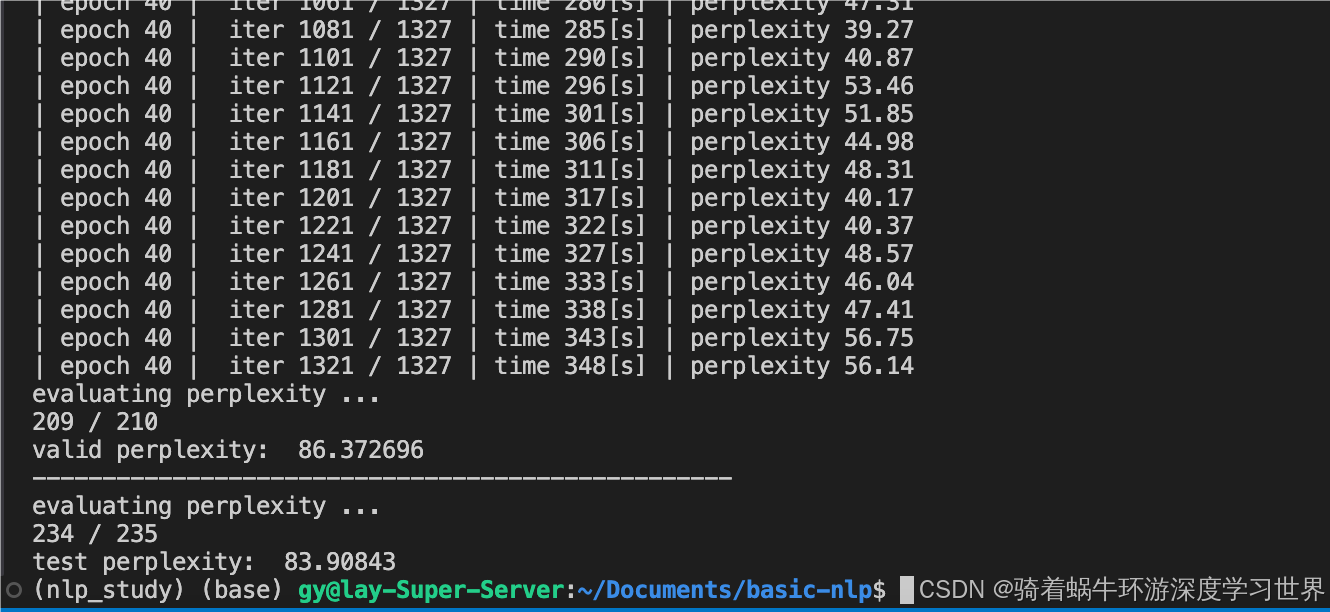
以下是实验结果：