一、插入排序

1.1 直接插入排序

        空间复杂度：。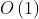

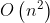
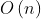
        时间复杂度：。在最好情况下，表中元素已经有序，此时每插入一个元素，都只需要比较一次而不用移动元素，因此时间复杂度为。

        稳定性：每次插入元素时总是从后向前先比较再移动，所以不会出现相同元素相对位置发生变化的情况。即直接插入排序是一个稳定的排序方法。

public class InsertSort {
     public static void insertSort(int[] array,int n) {
    	 int i=0;
    	 int j=0;
    	 for(i=1;i<n;i++) {//待排序的无序区
    		 int t=array[i];
    		 for(j=i-1;j>=0&&t<array[j];j--) {//已经排好序的有序区
    			 array[j+1]=array[j];
    		 }
    		 array[j+1]=t;
    	 }
     }
	public static void main(String[] args) {
		int[] a= {4,0,2,3,1};
		insertSort(a, 5);
		for(int n:a) {
			System.out.print(n+" ");
		}
	}
}

1.2 希尔排序

    空间复杂度：。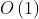

   时间复杂度：当n在某个特定范围时，希尔排序的时间复杂度约为。在最坏情况下希尔排序排序的时间复杂度为。

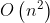
   稳定性：当相同关键字的记录被划分到不同的子表时，可能会改变他们之间的相对次序，因此希尔排序是一个不稳定的排序方法。

public static void shell(int value[],in