原文

1. 多分辨率分析

尽管时间和频率分辨率问题是物理现象（海森堡不确定性原理）的结果，并且无论使用哪种变换都存在，但是可以通过使用称为多分辨率分析（MRA）的替代方法来分析任何信号。 顾名思义，MRA可以分析具有不同分辨率的不同频率的信号，但不能像STFT那样对每个频谱分量进行均等的解析。

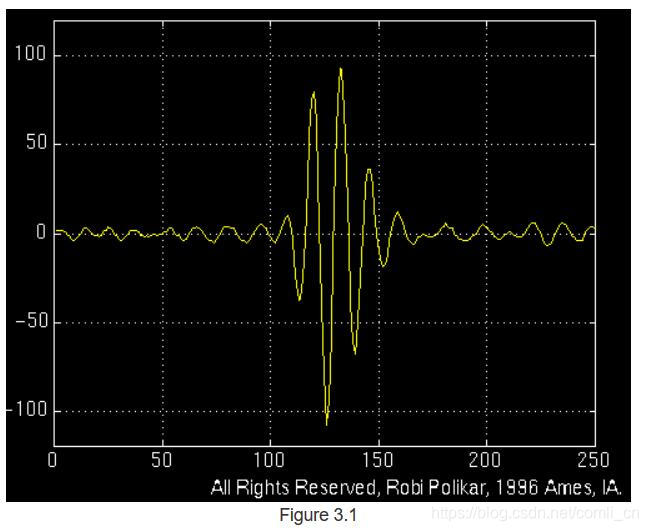
MRA被设计为在高频时具有良好的时间分辨率和较差的频率分辨率，在低频时具有良好的频率分辨率和较差的时间分辨率。 当手头信号在短时间内具有高频分量而在长时间内具有低频分量时，这种方法尤其有意义。 幸运的是，在实际应用中遇到的信号通常是这种类型的。 例如，下图显示了这种信号。 它在整个信号中具有相对较低的频率分量，并且在中间附近的短时间内具有较高的频率分量。

2. 连续小波变换

连续小波变换被开发为短时傅立叶变换的替代方法，以克服分辨率问题。 小波分析以与STFT分析类似的方式进行，在某种意义上，信号乘以一个函数$thewavelet$，类似于STFT中的窗口函数，并且针对不同的信号分别计算变换时域信号的片段。 但是，STFT和CWT之间有两个主要区别：

(1)没有对窗口信号进行傅立叶变换，因此将看到对应于正弦波的单个峰，即，不计算负频率。
(2) 在为每个单个频谱分量计算变换时，窗口的宽度会发生变化，这可能是小波变换的最重要特征。

连续小波变换定义如下:

$CW{T}_x^{\psi }(\tau ,s)={\Psi }_x^{\psi }(\tau ,s)=\frac{1}{\sqrt{|s|}}\int x(t){\psi }^{\ast }\left(\frac{t-\tau }{s}\right)dt$

如上式所示，变换后的信号是两个变量$\tau$和s的函数，分别是" translation"和"scale"参数。 $\psi (t)$是变换函数，称为母小波( mother wavelet)。 术语“母小波”之所以得名，是因为小波分析的两个重要属性，如下所述：

wavelet一词是指small wave。 small 是指此（窗口）函数具有有限长度（得到紧凑支持）的条件。wave是指该函数具有振荡性的条件。 术语“mother”表示在转换过程中使用的具有不同支持区域的函数是从一个主要函数或“母小波”派生的。 换句话说，母小波是用于生成其他窗口函数的原型。

术语" translation"的含义与STFT中使用的含义相同； 它与窗口的位置有关，因为窗口在信号中移动。 显然，该术语对应于变换域中的时间信息。 但是，我们没有STFT之前的频率参数。 取而代之的是，我们将"scale"参数定义为$\frac{1}{frequency}$。 术语"frequency"是为STFT保留的。 下一部分将更详细地说明"scale"。

3. The Scale

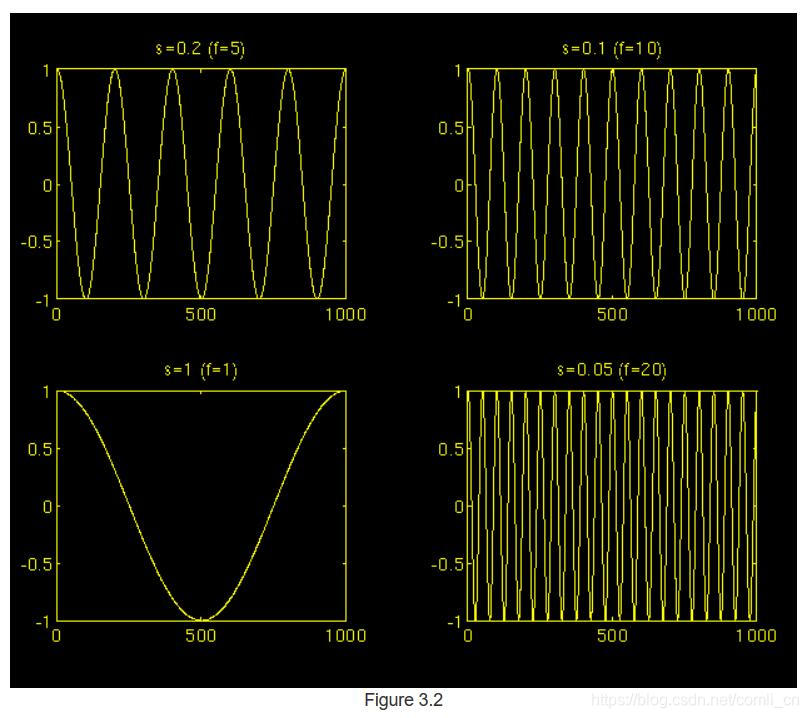
小波分析中的参数“scale”似于地图中使用的“scale”。 与地图的情况一样，“high scale”对应于（信号的）非详细全局视图，而“low scale”对应于详细视图。 同样，就频率而言，低频（“high scale”）对应于信号的全局信息（通常跨越整个信号），而高频（“low scale”）对应于信号中隐藏模式的详细信息（ 通常会持续相对较短的时间）。 下图给出了对应于各种刻度的余弦信号的示例。

幸运的是，在实际应用中，“ low scales”（高频）不会在信号的整个持续时间内持续存在，与图中所示不同，但它们通常会不时出现为短脉冲或尖峰。 “high scale”（低频）通常会持续整个信号持续时间。

缩放（Scaling）作为一种数学运算，可以放大或压缩信号。 较大的"scale"对应于扩张（或扩展）的信号，较小的"scale"对应于压缩的信号。 图中给出的所有信号均来自相同的余弦信号，即它们是同一功能的扩张或压缩版本。 在上图中，s = 0.05是最小比例，而s = 1是最大比例。

在数学函数方面，如果$f(t)$是给定函数，则在s> 1的情况下，$f(st)$对应于$f(t)$的压缩（压缩）版本，而在s<1时，对应于f（t）的扩展（扩张）版本 。

然而，在小波变换的定义中，在分母中使用了比例项，因此，上述陈述的反义成立，即，比例尺s> 1放大信号，而比例尺s <1压缩信号。 此处对“scale”的解释将在全文使用。

4. CWT的计算

在本节中将解释上述方程式。 令$x(t)$是要分析的信号。 选择母小波作为该过程中所有窗口的原型。 使用的所有窗口都是母小波的放大（或压缩）版本和平移版本。 有许多用于此目的的功能。 Morlet小波和Mexican hat函数是两个候选者，它们用于示例的小波分析，这些示例将在本章后面介绍。

一旦选择了母小波，计算就从s = 1开始，并对小于和大于“1”的所有s值计算连续小波变换。 但是，根据信号，通常不需要完全转换。对于所有实际目的，信号都是带宽受限的，因此，在有限的比例尺间隔内进行变换计算通常是足够的。 在本研究中，使用了s的一些有限值区间，这将在本章后面介绍。

为了方便起见，该过程将从标度s = 1开始，并针对s的增加值继续进行，即，分析将从高频开始，朝低频进行。 s的第一个值将对应于压缩程度最高的小波。 随着s值的增加，小波将扩大。

将小波放在信号的开始处与time= 0对应的点处。将小波函数以“1”的比例乘以信号，然后在所有时间进行积分。 然后，将积分结果乘以常数$\frac{1}{\sqrt{s}}$。 该乘法是出于能量归一化的目的，因此变换后的信号在每个尺度上都将具有相同的能量。 最终结果是变换的值，即在时间零和标度s = 1处的连续小波变换的值。 换句话说，它是与时标平面中的$\mathbf{\tau }=0，s=1$对应的值。

然后将比例为s = 1的小波向右移$\tau$到位置$t=\mathbf{\tau }$，并计算上述等式以获得时间为$t=\tau$，s = 1的变换值。 频率平面。

重复该过程，直到小波到达信号的末端。 现在完成了时标平面上标度s = 1的一排点。

然后，s增加一个小值。 请注意，这是一个连续的变换，因此$\mathbf{\tau }$和$s$都必须连续递增。 但是，如果此转换需要由计算机计算，则两个参数都将增加足够小的步长。 这对应于对时标平面进行采样。

对s的每个值重复上述过程。 给定s值的每次计算都将填充时标平面的相应单行。 当针对s的所有期望值完成该过程时，已计算出信号的CWT。

下图逐步说明了整个过程。

在图3.3中，显示了$\mathbf{\tau }$四个不同值的信号和小波函数。 该信号是图3.1所示信号的截断版本。 “scale"值为1，对应于最低"scale"或最高频率。 请注意它有多紧凑（蓝色窗口）。 它应与信号中存在的最高频率分量一样窄。 小波函数的四个不同位置在图中显示为${\mathbf{t}}_{\mathbf{o}}=2，{\mathbf{t}}_{\mathbf{o}}=40，{\mathbf{t}}_{\mathbf{o}}=90和{\mathbf{t}}_{\mathbf{o}}=140$。 在每个位置，它都乘以信号。 显然，乘积仅在信号落在小波支持区域内时才为非零，在其他地方为零。 通过在时间上移动小波，可以在时间上定位信号，通过更改s的值，可以在"sacle”（频率）上定位信号。

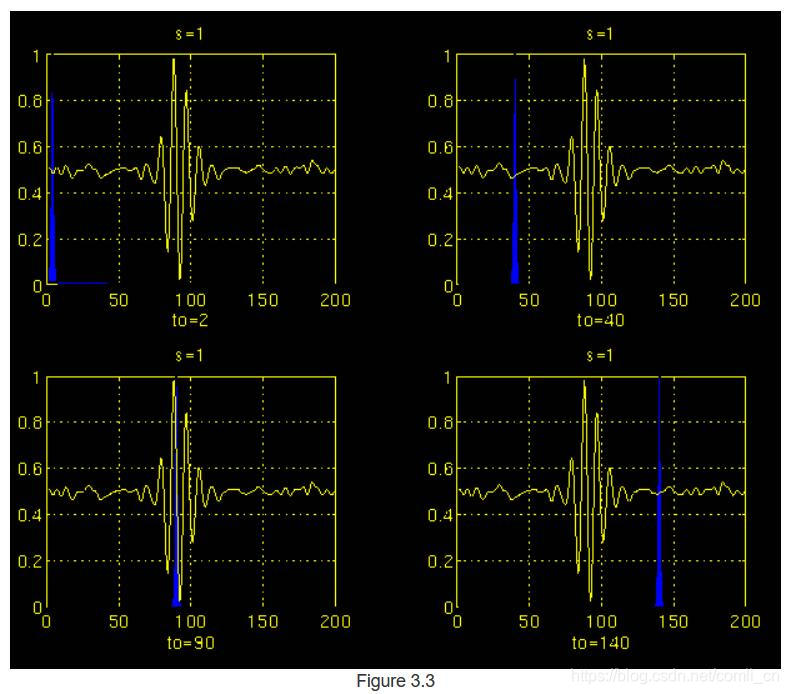
如果信号的频谱分量对应于s的当前值（在这种情况下为1），则小波与该频谱分量存在的位置处的信号的乘积将给出一个较大的值。 如果信号中不存在与s的当前值相对应的频谱分量，则乘积值将相对较小或为零。 图3.3中的信号的频谱分量与t = 100 ms周围s = 1时窗口的宽度相当。

图3.3中信号的连续小波变换将在100 ms左右的时间产生小范围的大数值，而在其他地方产生小数值。 另一方面，对于"high scale"，连续小波变换将在信号的整个持续时间内给出较大的值，因为低频始终存在。

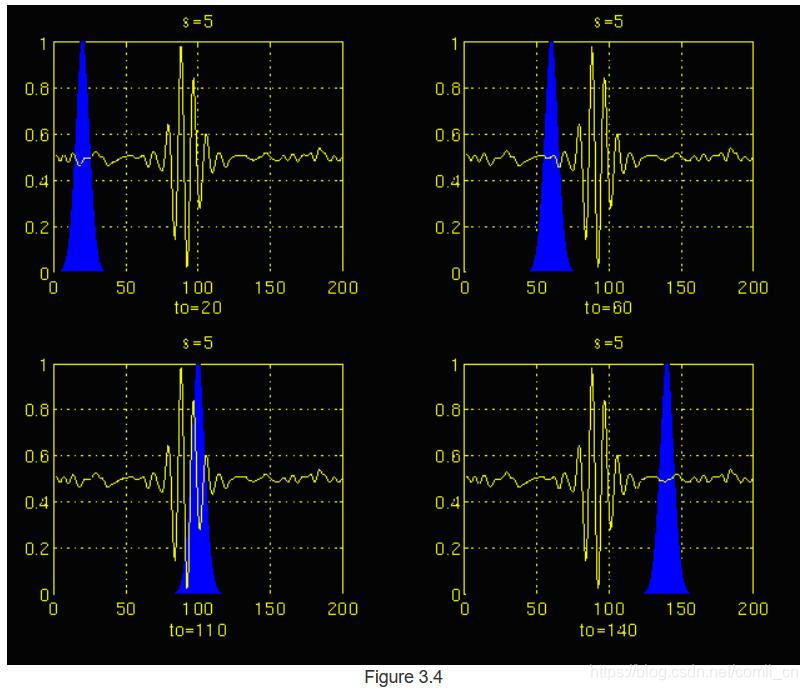
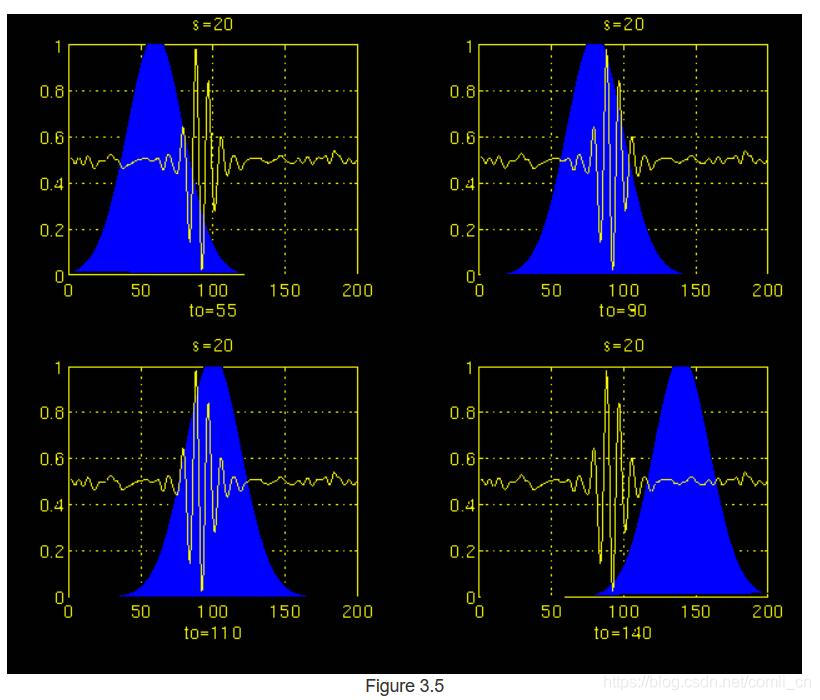
图3.4和3.5分别说明了标度s = 5和s = 20的相同过程。 请注意窗口宽度如何随比例增加（频率减少）而变化。 随着窗口宽度的增加，变换开始拾取低频分量。

结果，对于每个刻度和每个时间（间隔），将计算时标平面的一个点。 在一个尺度上的计算构成了时标平面的行，而在不同尺度上的计算构成了时标平面的列。

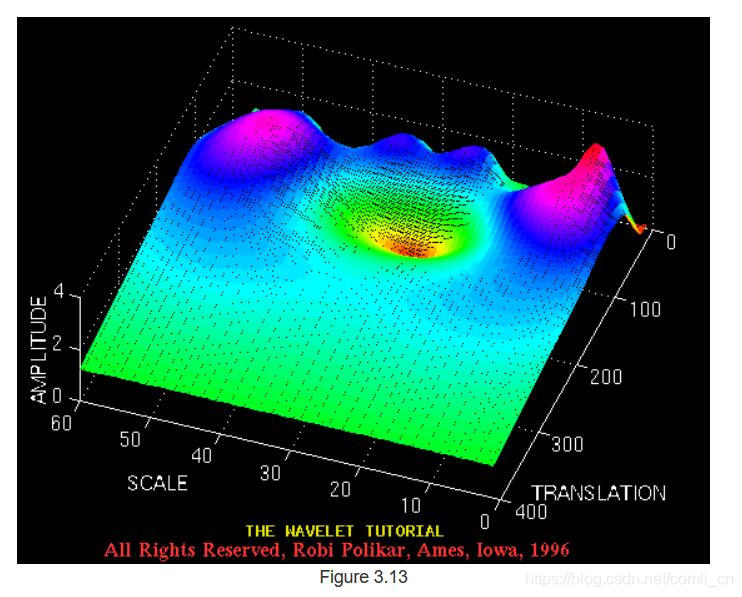
现在，让我们看一个例子，看看小波变换的真实外观。 考虑图3.6中的非平稳信号。 除了在不同的频率外，这类似于为STFT给出的示例。 如图所示，信号由30 Hz，20 Hz，10 Hz和5 Hz的四个频率分量组成。
图3.7是该信号的连续小波变换（CWT）。 请注意，轴是“translation” 和“scale”，而不是时间和频率。 但是，“translation” 与时间严格相关，因为它指示了子小波所在的位置。 可以将母小波的“translation” 视为从t = 0开始经过的时间。 然而，“scale”却完全不同。 请记住，公式3.1中的“scale”参数s实际上是频率的倒数。 换句话说，无论我们说的关于频率分辨率的小波变换的性质如何，它的反面都会出现在表示时域信号WT的图中。

请注意，在图3.7中，较小的“scale”对应于较高的频率，即，频率随着“scale”的增加而减小，因此，图中“scale”在零附近的部分实际上对应于分析中的最高频率，而“scale”较高的那部分对应于最低的频率 频率。 请记住，信号首先具有30 Hz（最高频率）分量，然后以最低标度从0到30的转换出现。然后是20 Hz分量，第二最高频率，依此类推。 5 Hz分量出现在“translation” 轴的末端（如预期的那样），并且按预期再次出现在较高的音阶（较低的频率）上。

现在，回想一下这些分辨率属性：与STFT在所有时间和频率下均具有恒定的分辨率不同，WT在高频下具有良好的时间和较差的频率分辨率，而在低频下具有良好的频率和较差的时间分辨率。图3.8从另一个角度显示了图3.7中的相同WT，以更好地说明分辨率属性：在图3.8中，“low scale”（较高的频率）具有较好的scale分辨率（scale更窄，这意味着scale的确切值不那么模棱两可），这对应于较差的频率分辨率。同样，“high scale”具有scale频率分辨率，它对应于较低频率的更好的频率分辨率。

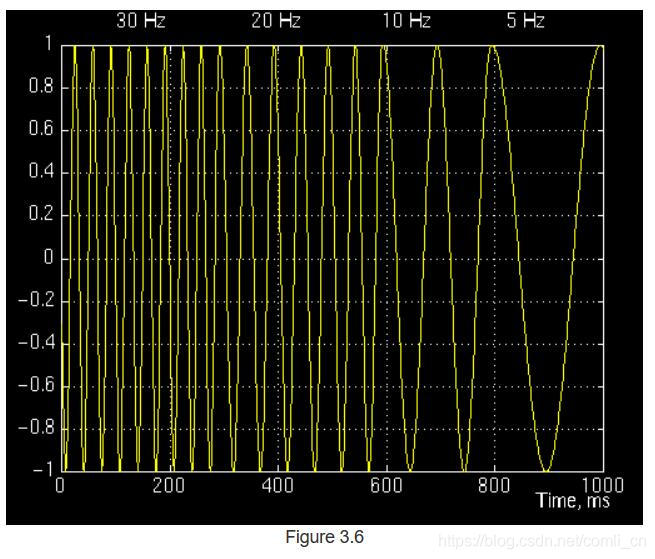
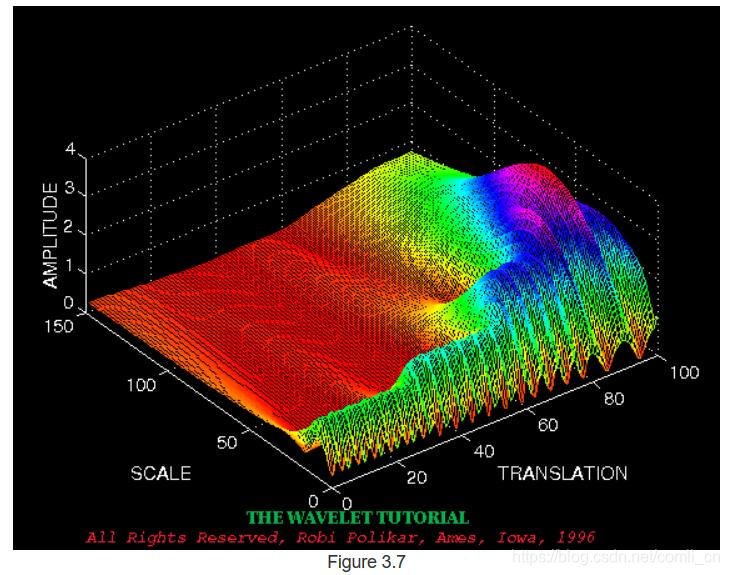
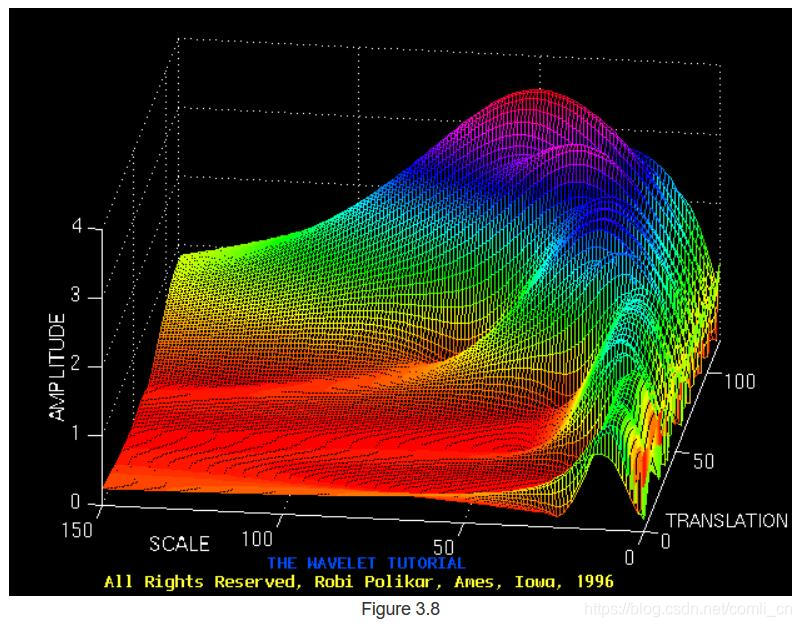
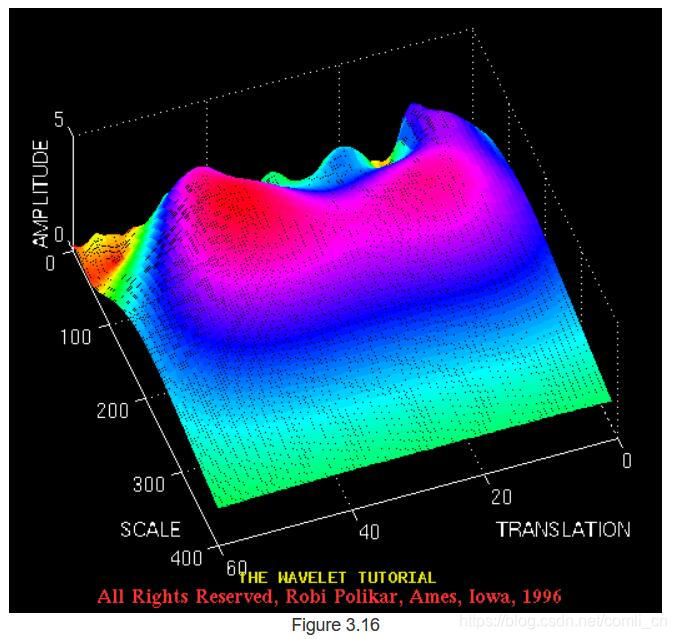
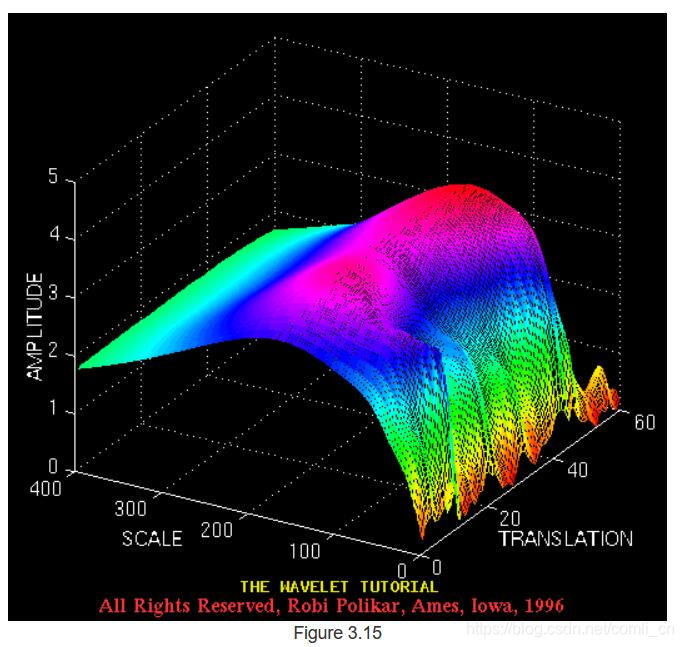
图3.7和3.8中的轴已标准化，应进行相应评估。大致来说，平移轴上的100点对应于1000 ms，而刻度轴上的150点对应于40 Hz的频带（平移和刻度轴上的数字分别不对应于秒和Hz，它们只是计算中的样本数）。

5. 时间和频率分辨率

在本节中，我们将仔细研究小波变换的分辨率属性。 请记住，分辨率问题是我们从STFT切换到WT的主要原因。

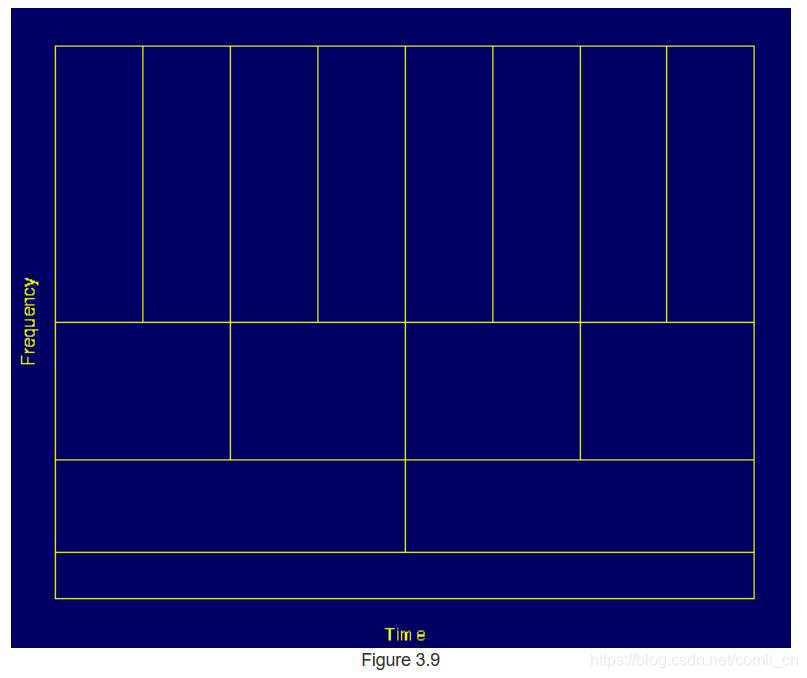
图3.9中的插图通常用于描述 如何解释时间和频率分辨率。 图3.9中的每个方框都对应于时频平面中的小波变换的值。 请注意，框具有某个非零区域，这意味着无法知道时频平面中特定点的值。 时频平面中落入一个框内的所有点都由WT的一个值表示。

让我们仔细看看图3.9：首先要注意的是，尽管盒子的宽度和高度会发生变化，但面积是恒定的。 也就是说，每个框代表时频平面的相等部分，但对时间和频率给出不同的比例。 请注意，在低频情况下，盒子的高度较短（对应于较好的频率分辨率，因为确切频率值的模棱两可性较小），但它们的宽度较长（这与较差的时间分辨率相对应，因为确切时间的值存在更多歧义）。 在较高的频率下，盒子的宽度减小，即时间分辨率变好，而盒子的高度增加，即频率分辨率变差。

在结束本节之前，值得一提的是在STFT情况下分区是什么样子的。 回想一下，在STFT中，时间和频率分辨率由分析窗口的宽度决定，该宽度对于整个分析都是固定的，即时间和频率分辨率都是恒定的。 因此，在STFT情况下，时频平面由正方形组成。

无论盒子的尺寸如何，STFT和WT中所有盒子的面积都是相同的，并由海森堡不等式确定。 总之，对于每个窗口函数（STFT）或母小波（CWT），框的面积是固定的，而不同的窗口或母小波会导致不同的面积。 但是，所有区域都由$\frac{1}{4}\mathbf{\pi }$限制。 也就是说，由于海森堡的不确定性原理，我们无法尽可能地减少盒子的面积。 另一方面，对于给定的母小波，可以更改盒子的尺寸，同时保持面积不变。 这正是小波变换所做的。

6. 小波理论：一种数学方法

本节介绍了小波分析理论的主要思想，也可以将其视为大多数信号分析技术的基本概念。傅里叶定义的FT使用基本函数来分析和重构函数。向量空间中的每个向量都可以写成该向量空间中基本向量的线性组合，即，将向量乘以某个常数，然后取乘积之和。信号分析涉及对这些常数的估计（变换系数或傅立叶系数，小波系数等）。合成或重构对应于计算线性组合方程。

与该主题相关的所有定义和定理都可以在Keiser的书《小波友好指南》中找到，但是对于基础函数如何工作的入门级知识对于理解小波理论的基本原理是必需的。因此，此信息将在本节中介绍。

7. 基础向量

向量空间V的基是一组线性独立的向量，因此V中的任何向量v都可以写成这些基向量的线性组合。 向量空间可能有多个基础。 但是，它们全部具有相同数量的向量，该数目称为向量空间的维数。 例如，在二维空间中，基础将具有两个向量。

$v=\sum _k{\nu }^k{b}_k$·········································································(3.2)

公式3.2展示了如何将任何向量v表示为基向量${\mathbf{b}}_{\mathbf{k}}$和相应系数${\mathbf{\nu }}^{\mathbf{k}}$的线性组合。

通过用基函数${\mathbf{\varphi }}_{\mathbf{k}}(\mathbf{t})$替换基向量${\mathbf{b}}_{\mathbf{k}}$，并用函数$f(t)$替换向量$v$，可以很容易地将这种就矢量而言的概念推广为函数 。 公式3.2变为

$f(t)=\sum _k{\mu }_k{\varphi }_k(t)$·······························································(3.2-a)

复指数函数（正弦和余弦）是FT的基本函数。 此外，它们是正交函数，为重构提供了一些理想的属性。

令$f(t)$和$g(t)$是$L^2[a，b]$中的两个函数。 （$L^2[a，b]$表示区间[a，b]中的平方可积函数的集合）。 两个函数的内积由公式3.3定义：

$<f(t),g(t)>={\int }_a^{b}f(t)\cdot g^{\ast }(t)dt$········································(3.3)

根据内积的上述定义，可以将CWT视为具有基函数${\psi }_{(\tau ,s)}(t)$的测试信号的内积：

$CW{T}_x^{\psi }(\tau ,s)={\Psi }_x^{\psi }(\tau ,s)=\int x(t)\cdot {\psi }_{\tau ,s}^{\ast }(t)dt$ ·····················(3.4)

其中：

${\psi }_{\tau ,s}=\frac{1}{\sqrt{s}}\psi \left(\frac{t-\tau }{s}\right)$······························································(3.5)

CWT的这一定义表明，小波分析是对基函数（小波）和信号本身之间相似度的度量。 在此，相似性是指相似的频率含量。 计算出的CWT系数是指在当前尺度下信号与小波的接近程度。

这进一步澄清了先前关于信号与小波在一定规模上的相关性的讨论。 如果信号具有对应于当前标度的频率的主要分量，则当前标度的小波（基函数）将与该频率分量出现的特定位置处的信号相似或接近。 因此，在time-scale平面上此时计算的CWT系数将是一个相对较大的数字。

8. 内积，正交性和正交性

如果两个向量v，w的内积等于零，则称它们正交

$<v,w>=\sum _n{v}_n{w}_n^{\ast }=0$··························································· ······(3.6)

类似地，如果两个函数f和g的内积为零，则称它们彼此正交：

$<f(t),g(t)>={\int }_a^{b}f(t)\cdot g^{\ast }(t)\cdot dt=0$············································(3.7)

如果向量${\mathbf{v}}_1，{\mathbf{v}}_2，....，{\mathbf{v}}_{\mathbf{n}}$的集合是成对正交的，则它们成对相互正交，并且所有长度均为“ 1”。 可以表示为：

$<v_m,v_n>={\delta }_{mn}$············································································(3.8)

同样，如果满足以下条件，则一组函数${\varphi }_k(t)，k=1,2,3，...$是正交的:

${\int }_a^b{\varphi }_k(t)\cdot {\varphi }_l^{\ast }(t)\cdot dt=0,k\ne l$(正交条件)···········································(3.9)

和

∫ a b { ∣ ϕ k ( t ) ∣ } 2 d x = 1 \int_a^b \{ | \phi_k(t) | \}^2 dx = 1 ∫ab​{∣ϕk​(t)∣}2dx=1········································································(3.10)

或同等:

${\int }_a^b{\varphi }_k(t)\cdot {\varphi }_l^{\ast }(t)\cdot dt={\delta }_{kl}$································································(3.11)

其中，${\delta }_{kl}$是Kronecker delta函数，定义为：

${\delta }_{kl}=\{\begin{array}{ll}1,& k=l\\ 0,& k\ne l\end{array}$······································································(3.12)

如上所述，可能有不止一组基函数（或向量）。 其中，正交基函数（或向量）特别重要，因为它们在查找这些分析系数时提供了很好的特性。 正交正态基数允许使用正交正态性以非常简单明了的方式计算这些系数。

对于正交基，系数${\mu }_k$可以计算为

${\mu }_k=<f,{\varphi }_k>=\int f(t)\cdot {\varphi }_k^{\ast }(t)\cdot dt$···············································(3.13)

然后可以用公式3.2_a代入${\mu }_k$系数来重建函数$f(t)$。 这产生:

$f(t)=\sum _k{\mu }_k{\varphi }_k(t)={\sum }_k<f,{\varphi }_k>{\varphi }_k(t)$····································(3.14)

正交基可能不适用于可以使用通用版本双正交基的每种类型的应用程序。 术语“双正交”是指彼此正交的两个不同的基，但是每个都不形成正交集。

但是，在某些应用中，在这种情况下，可以使用双正交基。 框架是小波理论的重要组成部分，感兴趣的读者可以参考前面提到的Kaiser的书。

遵循与第2章中STFT相同的顺序，接下来介绍连续小波变换的一些示例。 示例中给出的数字是由编写用于计算CWT的程序生成的。

在结束本节之前，我想介绍两个在小波分析中常用的小波。 墨西哥帽小波定义为高斯函数的二阶导数：

$w(t)=\frac{1}{\sqrt{2\pi }\cdot \sigma }{e}^{\frac{-t^2}{2{\sigma }^2}}$········································································(3.15)

$\psi (t)=\frac{1}{\sqrt{2\pi }\cdot {\sigma }^3}\left(e^{\frac{-t^2}{2{\sigma }^2}}\cdot \left(\frac{t^2}{{\sigma }^2}-1\right)\right)$·················································(3.16)

Morlet小波定义为:

$w(t)=e^{iat}\cdot e^{-\frac{t^2}{2\sigma }}$······································································(3.16-a)

其中a是调制参数，$\sigma$是影响窗口宽度的缩放参数。

9. 例子

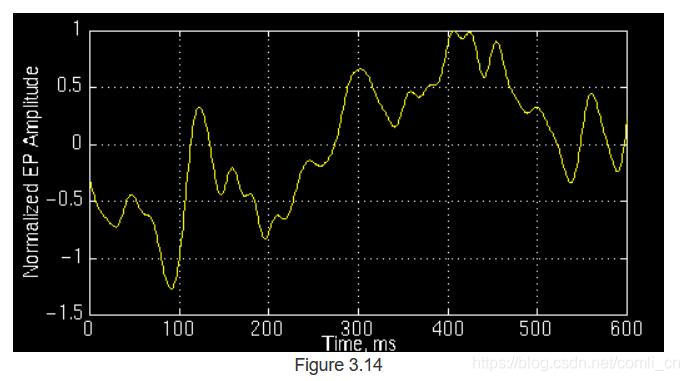
下面给出的所有示例均对应于现实生活中的非平稳信号。 这些信号来自数据库信号，其中包括正常人和患有阿尔茨海默氏病患者的事件相关电位。 由于这些不是简单的正弦波那样的测试信号，因此很难解释它们。 此处显示它们只是为了让您了解现实中的CWT到底是什么样子的。

图3.11所示的以下信号属于正常人。

以下是其CWT。 轴上的数字对我们并不重要。 这些数字只是表明CWT是在translation-scale平面上的350个translation和60个scale位置计算的。 这里要注意的重要一点是，该计算不是真正的连续WT，这从有限数量的位置处的计算可以明显看出。 这只是CWT的离散版本，将在本页后面解释。 但是请注意，这不是离散小波变换（DWT），这是本教程第四部分的主题。

图3.13从不同角度绘制了相同的变换，以实现更好的可视化。

图3.14绘制了被诊断患有阿尔茨海默氏病的患者的事件相关电位

图3.15说明了它的CWT：
这是从另一个角度来看的另一种观点：

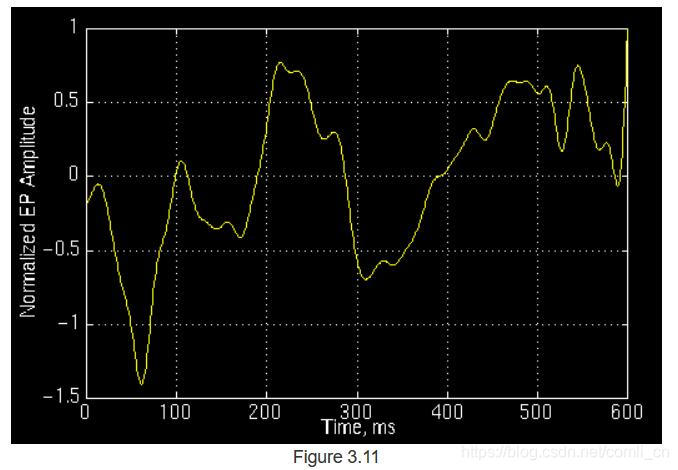
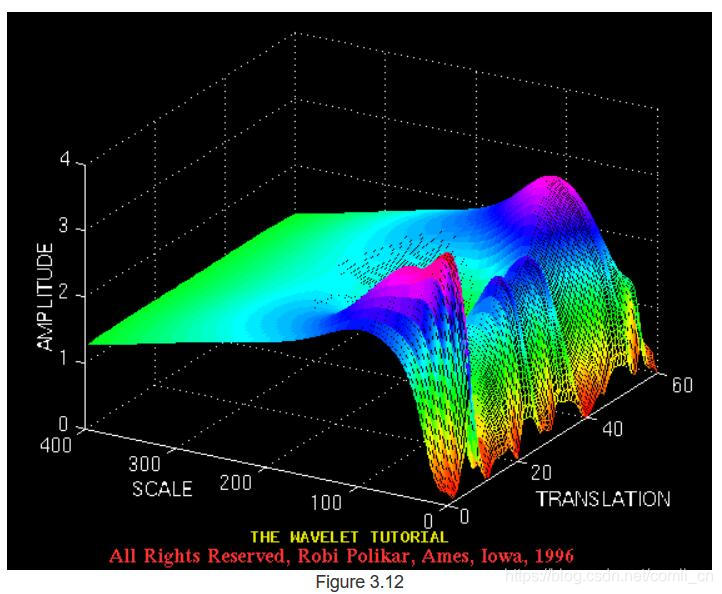
10.小波综合

只要满足公式3.18，连续小波变换就是可逆变换。 幸运的是，这是一个非限制性的要求。 即使基本函数通常可能不是正交的，如果满足公式3.18，连续小波变换也是可逆的。 通过使用以下重建公式，可以进行重建：

$x(t)=\frac{1}{C_{\psi }^2}{\int }_s{\int }_{\tau }\left[{\Psi }_x^{\psi }(\tau ,s)\frac{1}{s^2}\psi \left(\frac{t-\tau }{s}\right)\right]d\tau \cdot ds$··················（3.17）

其中$C_{\psi }$是一个常数，取决于所使用的小波。 重构的成功取决于此常数（可接纳性常数）是否满足以下可接纳性条件：

$C_{\psi }={\left\{2\pi {\int }_{-\infty }^{\infty }\frac{|\hat{\psi }(\xi ){|}^2}{|\zeta |}d\xi \right\}}^{\frac{1}{2}}<\infty$·····································(3.18)

其中$\hat{\psi }(\xi )$是$\psi (t)$的FT。 公式3.18表示$\hat{\psi }(0)=0$，这是

$\int \psi (t)\cdot dt=0$·······························································(3.19)

如上所述，公式3.19并不是一个严格的要求，因为可以找到许多积分为零的小波函数。 为了满足公式3.19，小波必须是振荡的。

11.连续小波变换的离散化：小波级数

在当今世界，计算机用于执行大多数计算（嗯，…好吧…几乎所有计算）。 显然，FT，STFT或CWT都无法通过使用解析方程，积分等来实际计算。因此，有必要离散化变换。 就像在FT和STFT中一样，最直观的方法是简单地对time-frequency (scale)平面进行采样。 更直观地讲，以均匀的采样率对time-frequency (scale)平面采样听起来是最自然的选择。 但是，在WT的情况下，可以使用缩放比例降低采样率。

根据Nyquist的规则，在"high scale"（较低的频率）下，可以降低采样率。 换句话说，如果需要"scale"${\mathbf{s}}_1$以${\mathbf{N}}_1$的采样率对time-scale平面进行采样，则可以在以下时间以${\mathbf{N}}_2$的采样率对同一平面进行采样 缩放${\mathbf{s}}_2$，其中${\mathbf{s}}_1<{\mathbf{s}}_2$（对应于频率${\mathbf{f}}_1>{\mathbf{f}}_2$）和${\mathbf{N}}_2<{\mathbf{N}}_1$。 ${\mathbf{N}}_1$和${\mathbf{N}}_2$之间的实际关系为:

$N_2=\frac{s_1}{s_2}{N}_1$···········································································(3.20)

$N_2=\frac{f_2}{f_1}{N}_1$···········································································(3.21)

换句话说，在较低的频率下，可以降低采样率，这将节省大量的计算时间。

然而，此时应注意，就信号分析而言，离散化可以任何方式进行而没有任何限制。 如果不需要合成，则甚至不需要满足奈奎斯特标准。 当且仅当需要信号重构时，对离散化和采样率的限制才变得重要。 奈奎斯特的采样率是允许从其离散采样中重建原始连续时间信号的最小采样率。 由于这个原因，前面提到的基向量特别重要。

如前所述，满足方程式3.18的小波$\mathbf{\psi }（\mathbf{\tau }，\mathbf{s}）$允许通过方程式3.17重构信号。 但是，对于连续变换而言确实如此。 问题是：如果离散化时间和比例参数，我们还能重构信号吗？ 在某些条件下，答案是“是”（正如他们在商业广告中经常说的：有一定的限制！！！）。

比例参数s首先在对数网格上离散。 然后将时间参数相对于比例参数离散化，即每个比例使用不同的采样率。 换句话说，采样是在图3.17所示的二元采样网格上完成的：

将轴所覆盖的区域视为整个时间刻度平面。 CWT为该平面上的连续点分配一个值。因此，存在无限数量的CWT系数。首先考虑scale轴的离散化。在对数无限的点中，使用对数规则仅取有限数。对数的底数取决于用户。由于其便利性，最常见的值为2。如果选择2，则仅刻度2、4、8、16、32、64等被计算。如果值为3，则刻度为3、9、27、81、243等可以被算出来。然后根据比例轴的离散化来离散时间轴。由于离散比例的变化是2倍，因此在每个比例上，时间轴的采样率都会降低2倍。

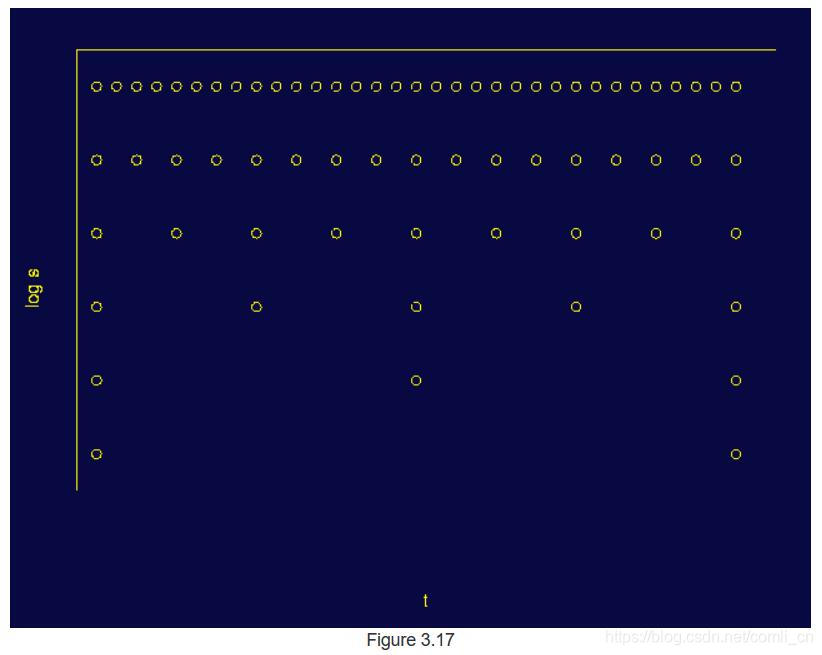
注意，在最小刻度（s = 2）上，仅采样了时间轴的32个点（对于图3.17中给出的特殊情况）。在下一个标度值s = 4处，由于标度增加了2倍，因此时间轴的采样率降低了2倍，因此仅采集了16个样本。下一步，s = 8，并及时获取8个样本，依此类推。

尽管它被称为time-scale平面，但将其称为translation-scale平面更为精确，因为变换域中的“时间”实际上对应于小波在时间上的移动。对于小波系列，实际时间仍然是连续的。

与连续傅立叶变换，傅立叶级数和离散傅立叶变换之间的关系相似，存在连续小波变换，半离散小波变换（也称为小波级数）和离散小波变换。

用数学术语表示上述离散化过程，scale离散化为$\mathbf{s}={\mathbf{s}}_0^{\mathbf{j}}$，translation离散化为$\mathbf{\tau }=\mathbf{k}\cdot {\mathbf{s}}_0^{\mathbf{j}}\cdot {\mathbf{\tau }}_0$其中${\mathbf{s}}_0>1$和${\mathbf{\tau }}_0>0$。 请注意，translation离散化是如何依赖于带有${\mathbf{s}}_0$的小数位数离散化的。

连续小波函数:

${\psi }_{\tau ,s}=\frac{1}{\sqrt{s}}\psi \left(\frac{t-\tau }{s}\right)$································································(3.22)

${\psi }_{j,k}(t)=s_0^{\frac{-j}{2}}\psi \left(s_0^{-j}-k{\tau }_0\right)$·················································(3.23)

通过插入$\mathbf{s}={\mathbf{s}}_0^{\mathbf{j}}$和$\mathbf{\tau }=\mathbf{k}\cdot {\mathbf{s}}_0^{\mathbf{j}}\cdot {\mathbf{\tau }}_0$。

如果$\left\{{\mathbf{\psi }}_{(\mathbf{j},\mathbf{k})}\right\}$构成正交基，则小波级数变换变为

${\Psi }_x^{{\psi }_{j,k}}=\int x(t){\psi }_{j,k}^{\ast }(t)dt$······················································(3.24)

或者：

$x(t)=c_{\psi }\sum _j\sum _k{\Psi }_x^{{\psi }_{j,k}}{\psi }_{j,k}(t)$············································`···(3.25)

小波级数要求${\mathbf{\psi }}_{(\mathbf{j},\mathbf{k})}$可以是正交，双正交或框架。 如果${\mathbf{\psi }}_{(\mathbf{j},\mathbf{k})}$不正交，则公式3.24变为:

${\Psi }_x^{{\psi }_{j,k}}=\int x(t)\widehat{{\psi }_{(j,k)}^{\ast }(t)}dt$····················································(3.26)

其中$\widehat{{\mathbf{\psi }}_{\mathbf{j},\mathbf{k}}^{\ast }(\mathbf{t})}$是双双正交基或双帧（请注意，*表示共轭）。

如果 { ψ ( j ,   k ) } \boldsymbol{ \{ \psi_{(j, \, k)} \} } {ψ(j,k)​}是正交或双正交的，则该变换将是非冗余的，就好像它们形成一个帧一样，该变换将是冗余的。 另一方面，查找框架比查找正交或双正交底物容易得多。

以下类推可能会清除此概念。 将整个过程视为查看特定对象。 人眼首先确定粗略视图，该粗略视图取决于眼睛到物体的距离。 这对应于调整比例参数${\mathbf{s}}_0^{-\mathbf{j}}$。 当观看非常接近的物体时，其细节非常丰富，j为负且较大（低比例，高频，分析信号中的细节）。 非常缓慢地移动头部（或眼睛），并以很小的增量（根据所观察的对象，其角度，距离）相应于$\mathbf{\tau }=\mathbf{k}\cdot {\mathbf{s}}_0^{\mathbf{j}}\cdot {\mathbf{\tau }}_0$。 请注意，当j为负且较大时，它对应于时间$\mathbf{\tau }$的小变化（高采样率）和${\mathbf{s}}_0^{\mathbf{j}}$的大变化（小比例，高频 ，其中采样率很高）。 比例参数也可以认为是放大倍数。

采样率有多低，仍然允许信号重构？ 这是优化程序要回答的主要问题。 发现最方便的值（就编程而言）对于$s_0$为“ 2”，对于$\tau$为“ 1”。 显然，当采样率被迫尽可能低时，可用正交小波的数量也会减少。

本章中给出的连续小波变换示例实际上是给定信号的小波序列。 根据信号选择参数。 由于不需要重建，因此对于不同的示例，采样率有时远低于临界值，其中$s_0$从2变为10，${\tau }_0$从2变为8。

到此结束本教程的第三部分。 希望您现在对小波变换的全部内容有一个基本的了解。 但是，还有一件事需要讨论。 即使离散小波变换可以在计算机上进行计算，根据信号大小和所需的分辨率，此计算可能需要几秒钟到几小时不等。 实际上，一种惊人的快速算法可用于计算信号的小波变换。 离散小波变换（DWT）在本教程的最后一章的第四部分中介绍。