概念
前提是数组有序
(假设数组非递减排列)步骤:
- 设左右指针left,right (左闭右闭区间)
- 找出中间的位置,如何判断该位置的值是否等于target
若nums[mid]==target,则返回该位置下标
若nums[mid]>target,则right=mid-1
若nums[mid]<target,则left=mid+1
mid的求法:mid=left+(right-left)/2或mid=left+((right-left)>>1)
注意:算数运算符的优先级比移位运算符高。
以上是常规思路,下面介绍另一种思路,这种思路太赞了
对于给定的一个单调递增数组
- 找出大于等于x的最小下标
分析:由于数组是单调递增的,可以把大于等于x的元素标记为绿色,小于x的元素标记为红色。
如下图:源自英雄哪里来
接下来,用两个游标,做一个规定,红色游标始终指向红色部分,绿色游标始终指向绿色部分。
对于一个长度为n的数组,l初始化为-1,r初始化为n(若l初始化0,考虑到当数组全为绿色时,l就指向了绿色部分,与规定相悖;若r初始化为n-1,考虑到当数组全为红色时,r就指向了红色部分,与规定相悖)。然后计算mid,若mid位置的值>=x,则将mid中的值标记为绿色部分即r=mid;若mid位置的值<x,则将mid中的值标记为红色部分即l=mid。
终止条件为l指向了红色部分的右边界,r指向了绿色部分的左边界,即(r-l)==1,总之,终止条件就是l+1=r。
int binarySearch(int* a, int n, int x) {
int l = -1;
int r = n;
while ((r-l) > 1) {
int mid = l + (r - l) / 2;
if (a[mid] >= x) {
r = mid;
}
else {
l = mid;
}
}
return r;
}
- 找出大于x的最小下标
和上一个的区别是将大于x的部分标记为绿色,小于等于x的部分标记为红色,最终找绿色的左边界即为大于x的最小下标。
int binarySearch(int* a, int n, int x) {
int l = -1;
int r = n;
while ((r-l) > 1) {
int mid = l + (r - l) / 2;
if (a[mid] >x) {
r = mid;
}
else {
l = mid;
}
}
return r;
}
- 找出小于等于x的最大下标
将小于等于x的标记为红色
int binarySearch(int* a, int n, int x) {
int l = -1;
int r = n;
while ((r-l) > 1) {
int mid = l + (r - l) / 2;
if (a[mid] >x) {
r = mid;
}
else {
l = mid;
}
}
return l;
}
- 找出小于x的最大下标
将小于x的部分标记为红色
int binarySearch(int* a, int n, int x) {
int l = -1;
int r = n;
while ((r-l) > 1) {
int mid = l + (r - l) / 2;
if (a[mid] >=x) {
r = mid;
}
else {
l = mid;
}
}
return l;
}
相关例题
- 1 二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
思路:直接二分查找就完了,这里采用第一种思路。
int search(vector<int>& nums, int target) {
int l,r;
l=0;
r=nums.size()-1;
while(l<=r){
int mid=l+(r-l)/2;
if(nums[mid]==target){
return mid;
}
else if(nums[mid]>target){
r=mid-1;
}
else{
l=mid+1;
}
}
return -1;
第二种思路 将大于target标为绿色,小于target的标为红色,找等于target的。
class Solution {
public:
int search(vector<int>& nums, int target) {
int n=nums.size();
int l=-1;
int r=n;
while((r-l)>1){
int mid=l+(r-l)/2;
if(nums[mid]==target){
return mid;
}
else if(nums[mid]>target){
r=mid;
}
else{
l=mid;
}
}
return -1;
}
};
- 2 搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例1
输入: nums = [1,3,5,6], target = 5
输出: 2
示例2
输入: nums = [1,3,5,6], target = 7
输出: 4
分析:根据题目描述,自然要用二分法,用第二种思路更方便,即找大于等于target的最小下标。
int searchInsert(vector<int>& nums, int target) {
int l=-1;
int r=nums.size();
while(r-l!=1){
int mid=l+(r-l)/2;
if(nums[mid]>=target){
r=mid;
}
else{
l=mid;
}
}
return r;
}
}
做完这两个题是不是二分挺简单的,再来个中等题巩固一下,冲!
- 3 34. 在排序数组中查找元素的第一个和最后一个位置
给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0
输出:[-1,-1]
思路:考虑以下几种情况
情况1.target比数组最小值(最左边的)还小或者比数组最大值(最右边的)还大。
情况2 target介于最大值最小值之间,且数组中不含target。
情况3 target介于最大值最小值之间,且数组中含target。
可以用两次二分法,分别找target的左边界和target的右边界,通过举例可以验证如果左边界>右边界对应情况1和2;如果左边界<=右边界对应情况3。这里我还是采用第二种思路。
int getRightBorder(vector<int>& nums, int target) {
int l = -1;
int r = nums.size();
while ((r - l) != 1) {
int mid = l + (r - l) / 2;
if (nums[mid] > target) {
r = mid;
}
else {
l = mid;
}
}
return l;
}
int getLeftBorder(vector<int>& nums, int target) {
int l, r;
l = -1;
r = nums.size();
while ((r - l) != 1) {
int mid = l + (r - l) / 2;
if (nums[mid] >= target) {
r = mid;
}
else {
l = mid;
}
}
return r;
}
void getRange(vector<int>& nums, int target) {
int l = getLeftBorder(nums, target);
int r = getRightBorder(nums, target);
vector<int> re(2);
if (l <= r) {//情况3
re[0]=l;
re[1]=r;
}
else {//情况1和2
re[0]=-1;
re[1]=-1;
}
return re;
}
- 4 寻找峰值
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
示例1
输入:nums = [1,2,3,1]
输出:2
解释:3 是峰值元素,你的函数应该返回其索引 2。
示例2
输入:nums = [1,2,1,3,5,6,4]
输出:1 或 5
解释:你的函数可以返回索引 1,其峰值元素为 2;
或者返回索引 5, 其峰值元素为 6。
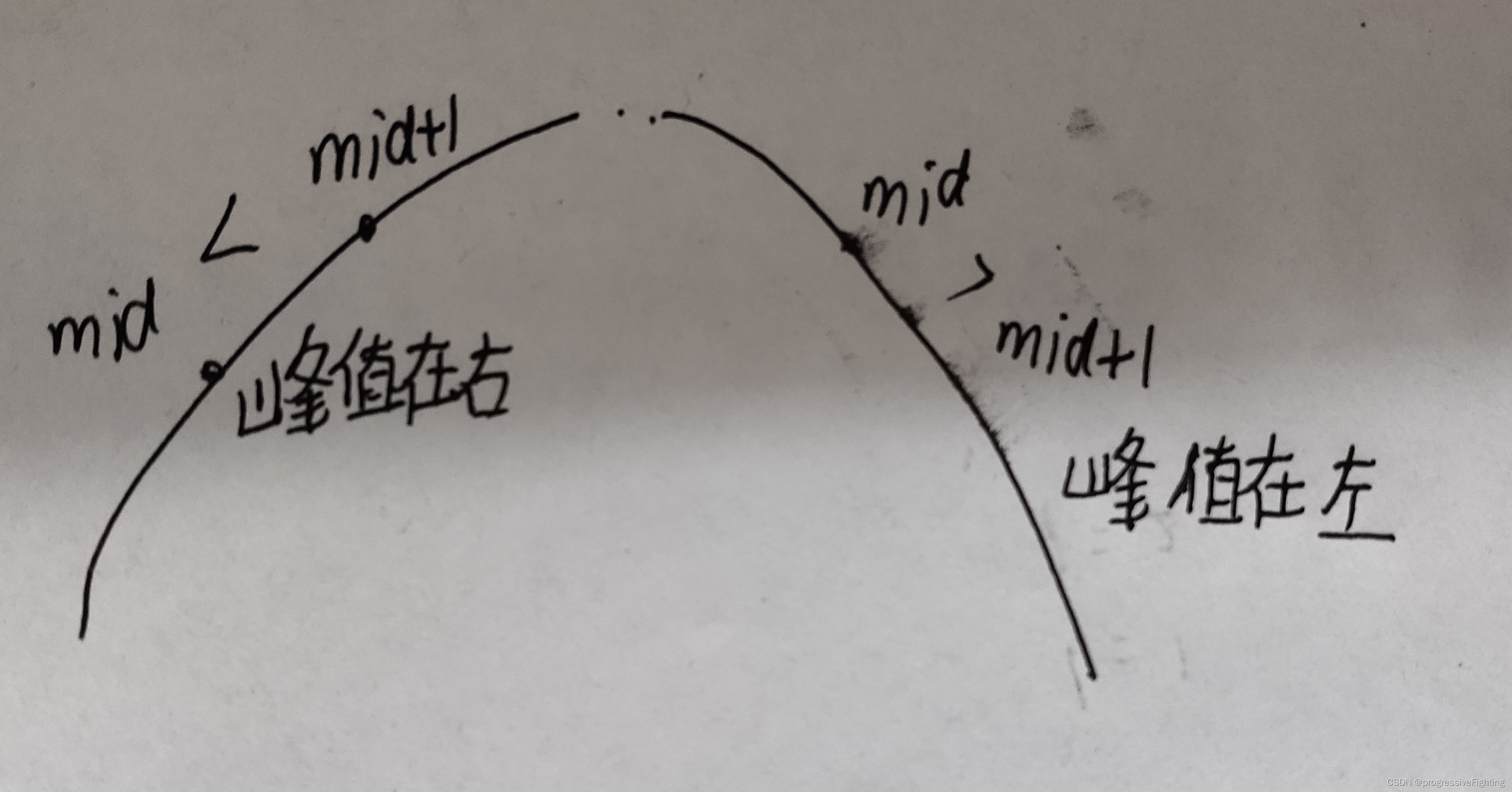
分析:此题乍一看给出的数组不是有序的,所以肯定不能用二分搜索,此言差矣,请再读一下题,找出峰值的位置,什么是峰值?峰值比两边的值都大,考虑局部的有序,若找到一个峰值,那么峰值和峰值右边的构成有序,同理峰值和峰值左边的构成有序,哎,这不出现有序了,嘿嘿!所以如果a[mid]<a[mid+1],峰值应该在mid的右边,调整left的值;如果a[mid]>a[mid+1],峰值应该在mid+1的左边,调整right的值,直到left和right重合即找到峰值。
如下图所示(字丑凑合看吧)
class Solution {
public:
int findPeakElement(vector<int>& nums) {
int l=0;
int r=nums.size()-1;
while(l<r){//结束的条件l=r
int mid=l+(r-l)/2;
if(nums[mid]<nums[mid+1]){
l=mid+1;
}else{
r=mid;
}
}
return l;
}
};
- 5 有效的完全平方数
给定一个 正整数 num ,编写一个函数,如果 num 是一个完全平方数,则返回 true ,否则返回 false 。
进阶:不要 使用任何内置的库函数,如 sqrt 。
示例 1:
输入:num = 16
输出:true
示例 2:
输入:num = 14
输出:false
思路:常规解法可以从1到num一个一个找,但考虑到高效性,可以尝试一下二分。如果mid2 >num,去mid左边找;如果mid2<num,去mid右边找;如果mid2==num,找到了直接返回true.
注意mid数据范围
class Solution {
public:
bool isPerfectSquare(int num) {
if(num==1){
return true;
}
int l=1;
int r=num;
while(l<=r){
unsigned long long mid=l+(r-l)/2;
if(mid*mid>num){
r=mid-1;
}
else if(mid*mid<num){
l=mid+1;
}
else if(mid*mid==num){
return true;
}
}
return false;
}
};
- 6 Sqrt(x)
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符
示例 1:
输入:x = 4
输出:2
示例 2:
输入:x = 8
输出:2
解释:8 的算术平方根是 2.82842…, 由于返回类型是整数,小数部分将被舍去。
思路:和上题大体上一样,需要注意的是最后要返回r,因为题目要求舍去小数部分,为什么返回r可以自己模拟一下。
class Solution {
public:
int mySqrt(int x) {
if(x<=1){
return x;
}
int l=1;
int r=x;
while(l<=r){
unsigned long long mid=l+(r-l)/2;
if(mid*mid<x){
l=mid+1;
}
else if(mid*mid>x){
r=mid-1;
}
else{
return mid;
}
}
return r;
}
};
总结
二分是一种方法,作为辅助性的手段,可以帮忙我们快速找到目标值。有时常规方法超时了而题目又要求线性时间复杂度时可以想想是否可以用二分。