【算法笔记】二叉树应用

前言

学习了二叉树的各大遍历以及基础知识，接下来开刷吧。这部分的题目不少，但认真刷完一定会有所收获，加油冲！！！

例题

解1 这其实也是层序遍历的应用，遍历每一层是先交换结点的左右孩子，然后将非空的左右结点入队。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        queue<TreeNode*> q;
        if(root==nullptr)return root;
        q.push(root);
        while(!q.empty()){
            int size=q.size();
            for(int i=0;i<size;i++){
                TreeNode* node=q.front();
                q.pop();
                TreeNode* temp=node->left;
                node->left=node->right;
                node->right=temp;
                if(node->left!=nullptr)q.push(node->left);
                if(node->right!=nullptr)q.push(node->right);
            }
        }
        return root;
    }
};

解2 递归

终止条件：空树返回0
参数以及返回值：root，返回当前树翻转后的根结点
本层递归：交换左右孩子结点

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(root==nullptr)return root;
        TreeNode* left=invertTree(root->right);//获取右子树的根结点（已翻转了的）
        TreeNode* right=invertTree(root->left);//获取左子树的根结点（已翻转了的）
        root->left=left;//调换左右孩子
        root->right=right;
        return root;
    }
};

590. N 叉树的后序遍历

解1 递归后序遍历
按照二叉树后序遍历的步骤，在遍历完孩子结点后，将根结点放在re中

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    void travel(Node* root,vector<int>& re){
        if(root==NULL)return ;
        vector<Node*> chs=root->children;
        int size=chs.size();
        for(int i=0;i<size;i++){
            travel(chs[i],re);

        }
        re.push_back(root->val);
    }
    vector<int> postorder(Node* root) {
        vector<int> re;
        travel(root,re);
        return re;
    }
};

解2 非递归后序遍历

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    vector<int> postorder(Node* root) {
        stack<Node*> st;
        vector<int> re;
        if(root==NULL)return re;
        st.push(root);
        while(!st.empty()){
            Node* node=st.top();
            st.pop();
            if(node!=NULL){
                vector<Node*> chs=node->children;
                st.push(node);
                st.push(NULL);
                for(int i=chs.size()-1;i>=0;i--){
                    st.push(chs[i]);
                }
            }
            else{
                node=st.top();
                st.pop();
                re.push_back(node->val);

            }
            
        }
        return re;
    }
};

101. 对称二叉树

解1 递归

确定参数和返回值：判断是否为对称二叉树就是判断左子树与右子树是否镜像对称，所以需要两个参数left，right。返回值就是bool，判断是否对称。
确定终止条件：这道题有多种终止条件，如果左子树或者右子树为空（左子树和右子树不全为空），则返回false；如果左子树的值不等于右子树的值，则返回false；如果左子树和右子树都为空，则返回true。
本层递归逻辑：除去终止条件，还剩左子树和右子树根结点的值相等的情况。因为是对称二叉树，所以左子树的左子树和右子树的右子树一样，左子树的右子树与右子树的左子树一样。只要这两种情况返回true，其余情况返回false

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool compare(TreeNode* left,TreeNode* right){
        if(left==nullptr && right!=nullptr)return false;
        else if(left!=nullptr && right==nullptr)return false;
        else if(left==nullptr && right==nullptr)return true;
        else if(left->val!=right->val)return false;
        else{//本层递归
            bool outside=compare(left->left,right->right);//其实还可以优化一下，如果outside是false的话就直接返回false，不用在跑下面的递归了
            bool inside=compare(left->right,right->left);
            return outside && inside;
        }
    }
    bool isSymmetric(TreeNode* root) {
        return compare(root->left,root->right);
    }
};

解2 队列实现，和递归逻辑基本一致

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        queue<TreeNode*>q;
        q.push(root->left);
        q.push(root->right);
        while(!q.empty()){
            TreeNode* leftNode=q.front();
            q.pop();
            TreeNode* rightNode=q.front();
            q.pop();
            if(leftNode==nullptr && rightNode==nullptr){//当前树对称
                continue;//注意不要break，这只是子树对称
            }
            if(leftNode==nullptr || rightNode==nullptr ||leftNode->val!=rightNode->val){//对应于递归的终止条件
                return false;
            }
            q.push(leftNode->left);//按左左、右右、左右、右左顺序入队
            q.push(rightNode->right);
            q.push(leftNode->right);
            q.push(rightNode->left);

        }
        return true;
    }
};

572. 另一棵树的子树
如果subRoot是root的子树，要么root和subRoot相等(判断两棵树是否相等)，要么subRoot是root->left的子树，要么subRoot是root->right的子树，这三个条件是与的关系。

递归：

参数以及返回值：参数两棵树的根结点，返回值bool
终止条件：如果root为空且subroot为空，则返回true；如果root和subroot有一个为空，则返回false。
本层递归：比较以当前结点作为根结点的树与subRoot是否一致，如果不一致再比较当前结点的左子树是否含有subRoot，如果没有再比较当前结点的右子树是否还有subRoot。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
     bool isEqual(TreeNode* p,TreeNode* q){
        if(p==nullptr && q==nullptr)return true;
        else if(p==nullptr || q==nullptr)return false;
        else if(p->val!=q->val)return false;
        else {
            bool leftNode=isEqual(p->left,q->left);
            bool rightNode=isEqual(p->right,q->right);
            return leftNode && rightNode;
        }
    }
    bool isSubtree(TreeNode* root, TreeNode* subRoot) {  
        if(root ==nullptr && subRoot==nullptr){
            return true;
        }
        else if(root==nullptr || subRoot ==nullptr){
            return false;
        }
        return isEqual(root,subRoot) || isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
    }
};

222. 完全二叉树的节点个数

这里运用满二叉树的性质求，如果k是树的深度，那么节点数2^k -1
完全二叉树中的存在满二叉树子树，所以当找到满二叉树子树时直接用公式求即可。
如果树的左子树的深度等于右子树的深度，那么该树为满二叉树。
递归：1. 确定参数及返回值：参数是root根结点，返回值是节点数。
2. 确定终止条件：如果root等于空节点，返回0.
3. 本层递归：求当前树的左右子树深度，判断左右子树深度是否相等，若相等，则按公式求；否则按一般求法，左子树的节点数+右子树的节点数+1

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        if(root==nullptr)return 0;

        int leftDepth=0;
        int rightDepth=0;
        TreeNode* leftNode=root->left;
        TreeNode* rightNode=root->right;
        while(leftNode!=nullptr){//计算左子树的深度
            leftNode=leftNode->left;
            leftDepth++;

        }
        while(rightNode!=nullptr){//计算右子树的深度
            rightNode=rightNode->right;
            rightDepth++;
        }
        if(leftDepth==rightDepth){//该树是满二叉树
            return (2<<rightDepth)-1;
        }
        return countNodes(root->left)+countNodes(root->right)+1;//
    }
};

110. 平衡二叉树

二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数。根结点的高度就是二叉树的深度，这也是常见的求树深度的方法
二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数。

递归：

确定参数和返回值：要判断是否为平衡二叉树，需要知道左右子树的深度和左右子树是否为AVL，参数可以是root，返回值是一个结构体，这个结构体包含树的深度和树是否为AVL。
终止条件：如果root==null，返回new Node(0,true)
本层递归：如果左右子树都为AVL且左右子树高度差不超过1，则返回new Node(height,true)；否则返回new Node(height,false)

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    struct Node{
        int height;
        bool avl;
        Node(int height,bool avl):height(height),avl(avl){}
    };
    Node* isAVL(TreeNode* root){
        if(root==nullptr)return new Node(0,true);
        Node* left=isAVL(root->left);
        Node* right=isAVL(root->right);
        int height=max(left->height,right->height)+1;
        if(left->avl && right->avl && abs(left->height-right->height)<=1){       
                return new Node(height,true);            
        }
        else{
            return new Node(height,false);
        }

    }
    bool isBalanced(TreeNode* root) {
        return isAVL(root)->avl;
    }
};

257. 二叉树的所有路径

递归：1.确定参数以及返回值，要求路径，第一个参数当前结点cur，第二个参数存放当前路径的结点，第三个参数存放所有的路径。求解路径时涉及到回溯，所以第二个参数用vector会比较方便。
2. 确定终止条件，当到达叶子结点时就终止，即结点的左右结点都为空。
3. 本层递归：求路径从根结点到叶子结点用前序遍历，将当前结点放入path，然后递归左子树，找完左子树的路径，然后回溯，递归右子树，再回溯。

递归后面紧挨着回溯。

用vector< int > 存放每条路径

/***
 *
 
 tion for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void travel(TreeNode* cur,vector<int>& path,vector<string>& re){
        path.push_back(cur->val);//中
        if(cur->left==nullptr && cur->right==nullptr){//终止条件，到了叶子节点
            string strs;
            for(int i=0;i<path.size()-1;i++){
                strs+=to_string(path[i]);//int转string
                strs+="->";
            }
            strs+=to_string(path[path.size()-1]);
            re.push_back(strs);
            return ;
        }

        if(cur->left!=nullptr){//左
            travel(cur->left,path,re);
            path.pop_back();//回溯
        }
        if(cur->right!=nullptr){//右
            travel(cur->right,path,re);
            path.pop_back();//回溯
        }

    }
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<int> path;
        vector<string> re;
        if(root==nullptr)return re;
        travel(root,path,re);
        return re;
    }
};

用string存放每条路径

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void travel(TreeNode* root,string paths,vector<string>& re){
        paths+=to_string(root->val);
        if(root->left==nullptr && root->right==nullptr){//到达叶子结点
            re.push_back(paths);
            return ;
        }
        if(root->left!=nullptr){
            paths+="->";
            travel(root->left,paths,re);
            paths.pop_back();//回溯，去掉"->"
            paths.pop_back();
        }
        if(root->right!=nullptr){
            paths+="->";
            travel(root->right,paths,re);
            paths.pop_back();
            paths.pop_back();
        }
        

    }
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> re;
        string paths;
        if(root==nullptr)return re;
        travel(root,paths,re);
        return re;
    }
};

迭代法
栈中放pair< TreeNode* ,string>，first放结点，second放当前路径，当遇到叶子结点再放re。注意空节点不要入栈

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> re;
        
        stack<pair<TreeNode*,string>> st;//first：结点，second：当前路径
        if(root==nullptr)return re;
        st.push(pair(root,to_string(root->val)));
        while(!st.empty()){
            TreeNode* node=st.top().first;
            string paths=st.top().second;
            st.pop();
           
            if(node->left==nullptr && node->right==nullptr){
                re.push_back(paths);
                
                continue;
            }
            
            if(node->right!=nullptr){
                paths+="->";
                st.push(pair(node->right,paths+to_string(node->right->val)));
                paths.pop_back();//回溯
                paths.pop_back();


            }
            if(node->left!=nullptr){
                paths+="->";
                st.push(pair(node->left,paths+to_string(node->left->val)));
                paths.pop_back();//回溯
                paths.pop_back();
            }
        }
        return re;
    }
};

404. 左叶子之和

左叶子：如果左节点不为空，且左节点没有左右孩子，那么这个节点就是左叶子，所以要判断是不是左叶子，需要根据父节点判断。
递归：1. 参数当前树的根结点，返回值是左叶子结点之和。
2. 终止条件：根结点为空，返回0
3. 本层递归：得到左子树的左叶子之和，右子树的左叶子之和，如果根结点的左结点也是左叶子，最终返回三者之和。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
        if(root==nullptr)return 0;
        int leftSumLeftLeaves=sumOfLeftLeaves(root->left);//左子树的左叶子之和
        int rightSumLeftLeaves=sumOfLeftLeaves(root->right);//右子树的左叶子之和
        int sum=0;
        if(root->left!=nullptr &&root->left->left==nullptr && root->left->right==nullptr){//判断root的左结点是否是左叶子
            sum+=root->left->val;
        }
        sum=sum+leftSumLeftLeaves+rightSumLeftLeaves;
        return sum;
    }
};

递归终止条件改为if(root->left==nullptr && root->right==nullptr){ return 0; } ，在计算左子树或右子树的左叶子之和就要加判断条件。如果左子树和右子树都为空，直接返回0.

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int travel(TreeNode* root){
        if(root->left==nullptr && root->right==nullptr){
            return 0;
        }
        int leftSum=0;
        int rightSum=0;
        if(root->left!=nullptr){
            leftSum=sumOfLeftLeaves(root->left);         
        }
        if(root->right!=nullptr){
            rightSum=sumOfLeftLeaves(root->right);
        }
        int sum=0;
        if(root->left!=nullptr && root->left->left==nullptr && root->left->right==nullptr){
            sum=root->left->val;
        }
        return leftSum+sum+rightSum;
    }
    int sumOfLeftLeaves(TreeNode* root) {
        if(root==nullptr){
            return 0;
        }
        return travel(root);
    }
};

迭代前序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
        stack<TreeNode*> st;
        int sum=0;
        if(root==nullptr)return sum;
        st.push(root);
        while(!st.empty()){
            TreeNode* node=st.top();
            st.pop();
            if(node->left!=nullptr && node->left->left==nullptr && node->left->right==nullptr){
                sum+=node->left->val;
            }
            if(node->right!=nullptr)st.push(node->right);
            if(node->left!=nullptr)st.push(node->left);
        }
        return sum;
    }
};

513. 找树左下角的值

层序遍历，先提前保存最左边的节点值，如何判断是否到了最底层

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int findBottomLeftValue(TreeNode* root) {
        queue<TreeNode*>q;
        q.push(root);
        int val;
        while(!q.empty()){
            int size=q.size();
            val=q.front()->val;//遍历结束就是最底最左的值
            for(int i=0;i<size;i++){
                TreeNode* node=q.front();
                q.pop();
                if(node->left!=nullptr){
                    q.push(node->left);
                }
                if(node->right!=nullptr){
                    q.push(node->right);
                }
            }
        }
        return val;
    }
};

递归：要找最底层左下角的结点，一是找到最底层，二是找到左下角，就拿示例2分析，根结点1的左子树的最底层左下角结点是4,1的右子树的最底层左下角结点是7，最终选择7是因为7的深度比4大，所以由此启发找深度最大的。

确定参数和返回值：确定是否到了最底层根据根结点就可以判断，所以参数就是根结点，返回值自定义一个类，类中包含当前树的深度和最底层左下角的结点的值。
终止条件：如果root为空，则返回Node(0,0)，如果root->left等于空且root->right等于空，找到了叶子结点，返回Node(1,root->val)
本层递归：得到左子树的最底层左下角的结点和右子树的最底层左下角的结点，比较height值，如果leftNode->height>=rightNode->height，则取leftNode作为最底部最左的结点。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    class Node{
        public:
        int height;
        int value;
        Node(int height,int value):height(height),value(value){}
    };
    Node* findNode(TreeNode* root){
        if(root==nullptr)return new Node(0,0);//只要保证height足够小就可以
        if(root->left==nullptr && root->right==nullptr)return new Node(1,root->val);//到达叶子结点
        Node* leftNode=findNode(root->left);//左子树的左下角
        Node* rightNode=findNode(root->right);//右子树的左下角
        if(leftNode->height>=rightNode->height){//如果左子树的深度>=右子树的深度，则取左子树最底层最左边结点的值作为当前树的最底层最左边结点
            return new Node(leftNode->height+1,leftNode->value);
        }
        else{//如果子树的深度<右子树的深度，则取右子树最底层最左边结点的值作为当前树的最底层最左边结点
            return new Node(rightNode->height+1,rightNode->value);
        }
        
    }
    int findBottomLeftValue(TreeNode* root) {
        return findNode(root)->value;
    }
};

if(root==nullptr)return new Node(0,0)这个条件也可以不加，同样也需要加判断，感觉这个好理解，终止条件就是叶子结点

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    struct Node{
        int height;
        int val;
        Node(int height,int val):height(height),val(val){}
    };
    Node* travel(TreeNode* root){
        if(root->left==nullptr && root->right==nullptr){//叶子结点直接返回root
            return new Node(1,root->val);
        }
        else if(root->left!=nullptr && root->right==nullptr){//左不空右空
            Node* left=travel(root->left);
            return new Node(left->height+1,left->val);
        }
        else if(root->left==nullptr && root->right!=nullptr){
            Node* right=travel(root->right);
            return new Node(right->height+1,right->val);
        }
        Node* left=travel(root->left);
        Node* right=travel(root->right);
        if(left->height>=right->height){//注意是大于等于
            return new Node(left->height+1,left->val);
        }
        else{
            return new Node(right->height+1,right->val);
        }


    }
    int findBottomLeftValue(TreeNode* root) {
        return travel(root)->val;
    }
};

112. 路径总和

递归：

参数和返回值：参数是根结点，计数值：每次减对应结点的值，初始值等于targetsum-root->val。
返回值是bool。
终止条件：如果该结点是叶子结点且count==0，则找到符合的路径，返回true；如果该结点是叶子结点且count！=0，则返回false。
本层递归：先找左结点到叶子结点是否符合，此时更新count的值，若符合，则返回true，若不符合，回溯则再找右结点到叶子结点是否符合，若符合，则返回true，否则返回false。(找到一个符合的就返回)

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool travel(TreeNode* root,int count){
        if(root->left==nullptr && root->right==nullptr && count==0){
            return true;
        }
        else if(root->left==nullptr && root->right==nullptr && count!=0){
            return false;
        }

        if(root->left!=nullptr){
            count-=root->left->val;
            if(travel(root->left,count)){
                return true;
            }
            count+=root->left->val;//回溯
        }
        if(root->right!=nullptr){
            count-=root->right->val;
            if(travel(root->right,count)){
                return true;
            }
            count+=root->right->val;
        }
        return false;
    }
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(root==nullptr)return false;
        return travel(root,targetSum-root->val);
    }
};

迭代
用栈模拟递归，由于要判断路径之和是否满足条件，所以栈中放pair<TreeNode*,int>，第一个表示结点，第二个表示当前路径之和。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        stack<pair<TreeNode*,int>>st;
        if(root==nullptr)return false;
        st.push(pair(root,root->val));
        while(!st.empty()){
            pair<TreeNode*,int> node=st.top();
            st.pop();
            if(node.first->left==nullptr && node.first->right==nullptr && node.second==targetSum){
                return true;
            }
            if(node.first->right!=nullptr){
                st.push(pair(node.first->right,node.second+node.first->right->val));
            }
            if(node.first->left!=nullptr){
                st.push(pair(node.first->left,node.second+node.first->left->val));
            }
        }
        return false;
    }
};

113. 路径总和 II

和上一个题差不多，这个是要找所有符合条件的路径，所以要遍历整棵树，因此不需要返回值，上一个则不需要遍历整棵树。
递归：1. 参数：根结点，计数值，当前的路径，存放所有的路径。不需要返回值
2. 终止条件：到达根结点且计数值为0，更新re，如果到达根结点但计数值不为空，不更新。
3. 本层递归：由于终止条件是叶子结点，所以避免空节点进入递归。先更新count，paths，然后递归左结点，然后回溯继续更新count，paths，调用右结点。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void travel(TreeNode* root,int count,vector<int> paths,vector<vector<int>>&re){
        if(root->left==nullptr && root->right==nullptr && count==0){
            re.push_back(paths);
            return ;
        }
        if(root->left==nullptr && root->right==nullptr && count!=0){
            
            return ;
        }

        if(root->left!=nullptr){
            count-=root->left->val;
            paths.push_back(root->left->val);
            travel(root->left,count,paths,re);
            paths.pop_back();
            count+=root->left->val;
        }
        if(root->right!=nullptr){
            count-=root->right->val;
            paths.push_back(root->right->val);
            travel(root->right,count,paths,re);
            paths.pop_back();
            count+=root->right->val;
        }
    }
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        vector<int>paths;
        vector<vector<int>> re;
        if(root==nullptr)return re;
        paths.push_back(root->val);
        travel(root,targetSum-root->val,paths,re);
        return re;
    }
};

106. 从中序与后序遍历序列构造二叉树

中序：左中右
后序：左右中
都剔除中间结点正好对应，所以划分后中序和后序长度依然相等
后序遍历的最后元素是中间结点，所以根据后序数组的最后一个元素将中序数组划分为左右两部分（不包括最后一个元素），然后根据划分后的中序数组来划分后序数组（同样也不包括最后一个元素即分割点）

递归：确定参数和返回值：参数：中序数组和后序数组，返回值：TreeNode*
终止条件：如果中序数组或者后序数组的元素为空（中序数组的尺寸和后序数组的尺寸一定相等），返回null；如果中序数组只要一个元素，说明该元素是叶子结点。
本层递归：找分割点在中序数组的位置，然后划分为左右两部分，然后划分后序数组，然后递归调用左右数组。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* travel(vector<int>& inorder,vector<int>& postorder){
        if(inorder.size()==0 || postorder.size()==0)return nullptr;
        int rootValue=postorder[postorder.size()-1];
        TreeNode* root=new TreeNode(rootValue);
        if(inorder.size()==1){//叶子结点
            return root;
        }
        int delimiterIndex;
        for(delimiterIndex=0;delimiterIndex<inorder.size();delimiterIndex++){//找中序数组的分割点
            if(inorder[delimiterIndex]==rootValue){
                break;
            }
        }
        //左闭右开区间划分中序数组
        vector<int> leftInorder(inorder.begin(),inorder.begin()+delimiterIndex);
        vector<int> rightInorder(inorder.begin()+delimiterIndex+1,inorder.end());//去除分割点
        postorder.resize(postorder.size()-1);//剔除后序数组最后一个元素，也就是中间结点的值
        //左闭右开区间以中序数组的尺寸划分后序数组
        vector<int> leftPostorder(postorder.begin(),postorder.begin()+leftInorder.size());
        vector<int> rightPostorder(postorder.begin()+leftInorder.size(),postorder.end());
        root->left=travel(leftInorder,leftPostorder);
        root->right=travel(rightInorder,rightPostorder);
        return root;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if(inorder.size()==0 || postorder.size()==0){
            return nullptr;
        }
        return travel(inorder,postorder);
    }
};

优化
由于第一种解法每次递归都要开辟4个vector，既费时间又费空间，其实只要明确数组的开始位置和结束位置就可，因此用下标表示即可。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* travel(vector<int>& inorder,int inorderBegin,int inorderEnd,vector<int>& postorder,int postorderBegin,int postorderEnd){//[inorderBegin,inorderEnd)，[postorderBegin,postorderEnd)
        if(inorderBegin==inorderEnd || postorderBegin==postorderEnd){
            return nullptr;
        }
        int rootValue=postorder[postorderEnd-1];
        TreeNode* root=new TreeNode(rootValue);
        if(inorderEnd-inorderBegin==1){//只有一个元素
            return root;
        }
        int delimiterIndex;
        for(delimiterIndex=inorderBegin;delimiterIndex<inorderEnd;delimiterIndex++){
            if(inorder[delimiterIndex]==rootValue){
                break;
            }
        }
        postorderEnd--;//剔除最后一个元素
        int leftInorderSize=delimiterIndex-inorderBegin;//划分后左中序数组的长度
        //左闭右开区间
        root->left=travel(inorder,inorderBegin,delimiterIndex,postorder,postorderBegin,postorderBegin+leftInorderSize);
        root->right=travel(inorder,delimiterIndex+1,inorderEnd,postorder,postorderBegin+leftInorderSize,postorderEnd);
        return root;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if(inorder.size()==0 || postorder.size()==0){
            return nullptr;
        }
        return travel(inorder,0,inorder.size(),postorder,0,postorder.size());
    }
};

左闭右开看着不得劲，再来个左闭右闭的

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* travel(vector<int>& inorder, int inBg,int inEg,vector<int>& postorder,int poBg,int poEg){
        if(inBg>inEg){
            return nullptr;
        }
        int rootVal=postorder[poEg];
        TreeNode* root=new TreeNode(rootVal);
        int dileIndex;
        for(int i=inBg;i<=inEg;i++){
            if(inorder[i]==rootVal){
                dileIndex=i;
                break;
            }
        }
        int left=dileIndex-inBg;
        root->left=travel(inorder,inBg,dileIndex-1,postorder,poBg,poBg+left-1);
        root->right=travel(inorder,dileIndex+1,inEg,postorder,poBg+left,poEg-1);
        return root;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        return travel(inorder,0,inorder.size()-1,postorder,0,postorder.size()-1);
    }
};

105. 从前序与中序遍历序列构造二叉树

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* travel(vector<int>& preorder,int preorderBegin,int preorderEnd,vector<int>& inorder,int inorderBegin,int inorderEnd){
        if(preorderBegin==preorderEnd || inorderBegin==inorderEnd){
            return nullptr;
        }
        int rootValue=preorder[preorderBegin];
        TreeNode* root=new TreeNode(rootValue);
        if(inorderEnd-inorderBegin==1){
            return root;
        }
        int delimiterIndex;
        for(delimiterIndex=inorderBegin;delimiterIndex<inorderEnd;delimiterIndex++){
            if(inorder[delimiterIndex]==rootValue)
            break;
        }
        preorderBegin++;
        int leftInorderSize=delimiterIndex-inorderBegin;
        root->left=travel(preorder,preorderBegin,preorderBegin+leftInorderSize,inorder,inorderBegin,delimiterIndex);
        root->right=travel(preorder,preorderBegin+leftInorderSize,preorderEnd,inorder,delimiterIndex+1,inorderEnd);
        return root;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if(preorder.size()==0 || inorder.size()==0){
            return nullptr;
        }
        return travel(preorder,0,preorder.size(),inorder,0,inorder.size());
    }
};

总结：
已知前序序列和中序序列或者已知后序序列和中序序列可以唯一确定一棵树。
但是已知前序序列和后序序列不能唯一确定一棵树，因为没有中序序列无法确定左右结点。

654. 最大二叉树

和上一题差不多，都是选择分裂位置，划分构造左右子树。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* travel(vector<int>& nums,int begin,int end){//左闭右闭区间   
        if(begin>end){
            return nullptr;
        }
        int delimiterIndex=begin;//分裂的下标
        int maxValue=nums[begin];//分裂值
        for(int i=begin;i<=end;i++){//找最大值
            if(nums[i]>maxValue){
                maxValue=nums[i];
                delimiterIndex=i;
            }                     
        }
        TreeNode* root=new TreeNode(maxValue);
        if(begin==end){//叶子结点
            return root;
        }
        root->left=travel(nums,begin,delimiterIndex-1);
        root->right=travel(nums,delimiterIndex+1,end);
        return root;
    }

    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        if(nums.size()<=0){
            return nullptr;
        }
        return travel(nums,0,nums.size()-1);
    }
};

617. 合并二叉树

明白了构造的规则就知道分4种情况：

都为空，根结点为空
root1 为空，root2 不为空，根结点为root2.
root1 不为空，root2 为空，根结点为空root1
都不为空，构造的根结点的值为两个根结点值之和，继续构造左右子树
递归：1. 参数：root1，root2 ，返回值：根结点
终止条件：对应前3中情况
本层递归：构造根结点，构造左子树，构造右子树

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if(root1==nullptr && root2==nullptr){//都为空
            return nullptr;
        }
       else if(root1==nullptr && root2!=nullptr){//左空右不空
           return root2;
       }
       else if(root1!=nullptr && root2==nullptr){//左不空右空
           return root1;
       }

       TreeNode* root=new TreeNode(root1->val+root2->val);//构造根结点
       root->left=mergeTrees(root1->left,root2->left);//构造左子树
       root->right=mergeTrees(root1->right,root2->right);//构造右子树
       return root;
    }
};

700. 二叉搜索树中的搜索

暴力搜索前序遍历，相等就返回

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        stack<TreeNode*> st;
        if(root==nullptr)return nullptr;
        st.push(root);
        while(!st.empty()){
            TreeNode* node=st.top();
            st.pop();
            if(node->val==val){
                return node;
            }
            if(node->right!=nullptr){
                st.push(node->right);
            }
            if(node->left!=nullptr){
                st.push(node->left);
            }
        }
        return nullptr;
    }
};

利用二叉搜索树的性质：

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
递归解法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if(root==nullptr)return nullptr;
        if(root->val==val)return root;
        if(root->val>val){
            return searchBST(root->left,val);
        }
        else{
            return searchBST(root->right,val);
        }
    }
};

迭代解法
由于二叉搜索的特殊性，不需要借助栈或者队列，如果当前根结点的值小于目标值，就去右子树找，如果当前根结点的值大于目标值，就去左子树找。直接用一个循环就可以。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        while(root!=nullptr){
            if(root->val==val)
            return root;
            else if(root->val>val)
            root=root->left;
            else 
            root=root->right;
        }
        return root;
        
    }
};

98. 验证二叉搜索树

二叉搜索树：根结点比左边的结点都要大，比右边的结点都要小，并且左右子树都为二叉搜索树
空树肯定是二叉搜索树，除去空树还有4种情况：

左右子树都空，即为叶子结点
左子树不空，右子树空
左子树空，右子树不空
左右子树都不空
因为要判断根结点比左边的所有结点都要大，因此需要保存左子树的最大值，只要保证根结点比左子树的最大值都要大即可；同样根结点比右边的所有结点都要小，因此还需要保存右子树的最小值，只要保证根结点比右子树的最小值还有小即可。
通过以上分析，可以建一个类Node，类中包含最大值，最小值，是否为二叉搜索树

接下来通过递归来解决

参数：根结点，返回值：Node*
终止条件:如果为叶子结点,直接返回Node，最大值最小值都为当前结点的值，当然是二叉搜索树
对后三种情况进行讨论：
这三种情况开始都要先判断左右子树是否为二叉搜索树，如果不是就直接返回

左子树不为空，右子树为空，判断根结点是否比左子树的最大值还要大，然后返回并更新最大值
左子树为空，右子树不为空，判断根结点是否比右子树的最小值还要小，然后返回并更新最小值
左右子树都不空，判断根结点是否比左子树的最大值大，比右子树的最小值小，然后返回更新最大值最小值。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    class Node{
        public:
        bool isBST;
        int max;
        int min;
        Node(bool isBST,int max,int min):isBST(isBST),max(max),min(min){}
         
    };
    Node* travel(TreeNode* root){
        if(root->left==nullptr && root->right==nullptr){//到达叶子结点
            return new Node(true,root->val,root->val);
        }
        else if(root->left!=nullptr && root->right==nullptr){//左不空右空，左边的结点比root都要小，所以root的最小值不变，最大值就是root
            Node* leftTree=travel(root->left);
            if(root->val > leftTree->max && leftTree->isBST){
                return new Node(true,root->val,leftTree->min);
            }
            else{
                return new Node(false,0,0);//只要isBST为false，max，min就没有意义了
            }
        }
         
        else if(root->left==nullptr &&root->right!=nullptr){//左空右不空，右边的结点比root都要大，所以root的最大值不变，最小值为root
            Node* rightTree=travel(root->right);
            if(root->val<rightTree->min && rightTree->isBST){
                return new Node(true,rightTree->max,root->val);
            }
            else{
                return new Node(false,0,0);
            }
        }
        Node* leftTree=travel(root->left);
        Node* rightTree=travel(root->right);
         if(root->val > leftTree->max && root->val < rightTree->min && leftTree->isBST && rightTree->isBST) {
            return new Node(true,rightTree->max,leftTree->min);
            
        }
        else{
            return new Node(false,0,0);
        }

    }
    bool isValidBST(TreeNode* root) {
        if(root==nullptr)return true;
        return travel(root)->isBST;
    }
};

上述解法确实做麻烦了，辛苦写下来的就当纪念吧！
简便做法，二叉搜索树中序遍历一定是递增排列的，所以可以中序遍历加判断
最小值初始化为LONG_MIN

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    long long maxVal = LONG_MIN;//long long 的最小值
    bool isValidBST(TreeNode* root) {
        if(root==nullptr)return true;
        bool leftTree=isValidBST(root->left);
        if(root->val <= maxVal || !leftTree){//不符合递增，或者左子树不为二叉搜索树
            return false;
        }
        maxVal=root->val;//更新最大值
        bool rightTree=isValidBST(root->right);
        return leftTree && rightTree; 

    }
};

迭代法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isValidBST(TreeNode* root) {
        stack<TreeNode*> st;
        long long maxVal=LONG_MIN;
        if(root==nullptr)return true;
        st.push(root);
        while(!st.empty()){
            TreeNode* node=st.top();
            st.pop();
            if(node!=nullptr){
                if(node->right!=nullptr)st.push(node->right);
                st.push(node);
                st.push(nullptr);
                if(node->left!=nullptr)st.push(node->left);
            }
            else{
                node=st.top();
                st.pop();
                if(node->val <= maxVal){
                    return false;
                }
                maxVal=node->val;
            }
        }
        return true;
    }
};

利用前后结点判断
中序遍历，并判断root的值是否比pre大

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* pre=nullptr;
    bool isValidBST(TreeNode* root) {
        if(root==nullptr)return true;
        if(!isValidBST(root->left)){//左子树不是二叉搜索树
            return false;
        }
        if(pre!=nullptr){
            if(root->val<=pre->val){//判断是否递增
                return false;
            }
        }
        pre=root;
        if(!isValidBST(root->right)){//右子树不是二叉搜索树
            return false;
        }
        return true;
    }
};

783. 二叉搜索树节点最小距离

遇到二叉搜索树求差值、最值就可以转化为数组上求最值。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int>re;
    void travel(TreeNode* root){//中序遍历，并将结点值保存在re
        if(root==nullptr){
            return ;
        }
        travel(root->left);
        re.push_back(root->val);
        travel(root->right);
    }
    int minDiffInBST(TreeNode* root) {
        travel(root);
        int minValue=re[1]-re[0];
        for(int i=2;i<re.size();i++){//遍历数组求得最小差值
            minValue=minValue<abs(re[i]-re[i-1])?minValue:abs(re[i]-re[i-1]);
        }
        return minValue;
    }
};

递归在遍历中求
中序遍历，需要保存当前结点的上一个结点，用来计算差值

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minValue=INT_MAX;
    TreeNode* pre=nullptr;//pre先初始化为空，只有不为空时才能计算差值
    void travle(TreeNode* root){
        if(root==nullptr)return ;
        travle(root->left);
        if(pre!=nullptr){
            minValue=minValue < root->val - pre->val?minValue:root->val - pre->val;
        }
        pre=root;
        travle(root->right);
    }
    int minDiffInBST(TreeNode* root) {
        travle(root);
        return minValue;
    }
};

迭代写法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDiffInBST(TreeNode* root) {
        stack<TreeNode*>st;
        int minValue=INT_MAX;
        st.push(root);
        TreeNode* pre=nullptr;
        while(!st.empty()){
            TreeNode* node=st.top();
            st.pop();
            if(node!=nullptr){
                if(node->right!=nullptr){
                    st.push(node->right);
                }
                st.push(node);
                st.push(nullptr);
                if(node->left!=nullptr){
                    st.push(node->left);
                }
            }
            else{
                node=st.top();
                st.pop();
                if(pre!=nullptr){
                     minValue=minValue<node->val-pre->val?minValue:node->val-pre->val;
                }
                pre=node;
            }
        }
        return minValue;
    }
};

501. 二叉搜索树中的众数

解1，使用于任何二叉树，先遍历整棵树统计元素的频率，然后输出频率最高的元素

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    typedef pair<int,int> P;
    unordered_map<int ,int>umap;//<元素，频率>
    vector<int>re;
    bool static compare(P p1,P p2){
        return p1.second>p2.second;//value值从大到小排列
    }  
    void travel(TreeNode* root){//前序遍历统计元素的频率
        if(root==nullptr){
            return ;
        }
        umap[root->val]++;
        travel(root->left);
        travel(root->right);
    }
    vector<int> findMode(TreeNode* root) {
        travel(root);
        vector<P>v1(umap.begin(),umap.end());
        sort(v1.begin(),v1.end(),compare);//按频率从大到小排序
        re.push_back(v1[0].first);//第一个一定是众数
        for(int i=1;i<v1.size();i++){
            if(v1[i].second==v1[0].second){
                re.push_back(v1[i].first);
            }
        }
    return re;
    }
};

解2利用二叉搜索树的性质：相同的元素一定是相邻的，每次比较相邻的两元素即可。
如果是有序数组统计元素的频率：从前往后遍历，每次比较当前元素与前一个元素是否相等，若相等count++，若不相等count=1.
如果是二叉搜索树，中序遍历，也是比较当前结点的值与前一结点的值，若相等，count++，若不相等，count=1。
和上一题一样设一个前结点pre，初始化为nullptr，若pre==nullptr，说明cur是最左下角的结点。
本题统计最大频率的元素（不止一个），最终要放在一个集合里
因此设两个变量，count元素的频率，maxCount最大频率，re存放结果
当count>maxCount，清空re，更新maxCount，然后将当前结点的值放入re
如果count==maxCount，将当前结点的值放入re
最终返回re即可。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int>re;
    int count=0;//元素频率
    int maxCount=0;//最大频率
    TreeNode* pre=nullptr;
    void travle(TreeNode* cur){
        if(cur==nullptr)return ;
        travle(cur->left);
        if(pre==nullptr){//最左下角的数
            count=1;
        }
        else if(cur->val==pre->val){
            count++;
        }
        else if(cur->val!=pre->val){
            count=1;
        }
        
        if(count==maxCount){
            re.push_back(cur->val);
        }
        if(count>maxCount){
            re.clear();//一定要记得清空之前的元素，之前的元素不再是频率最大的元素了
            maxCount=count;
            re.push_back(cur->val);
        }
        pre=cur;
        travle(cur->right);
    }
    vector<int> findMode(TreeNode* root) {
        travle(root);
        return re;
    }
};

解3 迭代写法和递归逻辑一样

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
	int count = 0;
	int maxCount = 0;
	vector<int>re;
	TreeNode* pre = nullptr;
	vector<int> findMode(TreeNode* root) {
        stack<TreeNode*>st;
		st.push(root);
		while (!st.empty()) {
			TreeNode* node = st.top();
			st.pop();
			if (node != nullptr) {
				if (node->right != nullptr) {
					st.push(node->right);
				}
				st.push(node);
				st.push(nullptr);
				if (node->left != nullptr) {
					st.push(node->left);
				}
			}
            else {
                node=st.top();
                st.pop();
                if(pre==nullptr){
                    count=1;
                }
                else if(node->val==pre->val){
                    count++;
                }
                else if(node->val!=pre->val){
                    count=1;
                }
                pre=node;
                if(count==maxCount){
                    re.push_back(node->val);
                }
                if(count>maxCount){
                    re.clear();
                    maxCount=count;
                    re.push_back(node->val);
                }
            }

		}
    return re;
	}
};

236. 二叉树的最近公共祖先

找最近的公共祖先自然要从底往上找，也就是后序遍历
如果某结点的左子树存在p，右子树存放q或者左子树存放q，右子树存在p，说明该结点为最近公共祖先。
接下来递归解决

参数：root，p，q
返回值：TreeNode* 当前树是否有p或者q结点，如果有则返回p或q结点，没有则返回空。
终止条件：当树为空时，返回null
当root等于p或者q，因为要找p q的公共祖先就没必要再往下找了，所以返回root
本层递归：先递归得到左子树的返回值和右子树的返回值，
如果left==NULL && right==NULL，说明没有p和q的公共祖先
如果left==NULL && right!=NULL,说明右子树有p或者q，直接返回right
如果left!=NULL && right==NULL，说明左子树有q或者p，直接返回left
如果都不为空，说明左子树有p，右子树有q或者左子树有q，右子树有p，返回root

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==NULL || root==q || root==p){
            return root;
        }
        TreeNode* left=lowestCommonAncestor(root->left,p,q);
        TreeNode* right=lowestCommonAncestor(root->right,p,q);
        if(left==NULL && right==NULL){
            return NULL;
        }
        else if(left==NULL && right!=NULL){
            return right;
        }
        else if(left!=NULL && right==NULL){
            return left;
        }
        else {
            return root;
        }

    }
};

235. 二叉搜索树的最近公共祖先

本题直接用上一题的代码就能通过但没啥意义嘛
考虑二叉搜索树的有序性，公共祖先应该是介于p和q之间，所以如果当前结点比pq都小，往右找，如果当前结点比pq都大，往左找，剩下的情况就是介于pq之间，此时root就是最近公共祖先。
这道题和上一题的区别是，本题不需要遍历整棵树，只需要根据比较结果找就可以了。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==NULL || root==q ||root==p){
            return root;
        }
        if(p->val <root->val && q->val<root->val){//pq都比root小，往左找
            return lowestCommonAncestor(root->left,p,q);
        }
        else if(p->val >root->val && q->val>root->val){//qp都比root大，往右找
            return lowestCommonAncestor(root->right,p,q);
        }
        else {//一大一小的情况，root就是最大公共祖先
            return root;
        }
    }
};

迭代写法，和递归逻辑一样

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */

class Solution {
public:
	TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
		while (root != NULL) {
			if (root == NULL || root == p || root == q) {
				return root;
			}
			else if (p->val < root->val && q->val < root->val) {
				root = root->left;
			}
			else if (p->val > root->val && q->val > root->val) {
				root = root->right;
			}
			else {
				return root;
			}
		}

		return root;
	}
};

701. 二叉搜索树中的插入操作

如果val>root->val,往右走，如果val< root->val.往左走，直到叶子结点
这里先用递归解决

参数：root，val，
返回值：TreeNode*,插入后的头结点
终止条件：当root为空值，返回new TreeNode(val)
本层递归：如果val>root->val，用一个变量接住右子树的返回值，然后root->right = right;.如果val < root->val,一个变量接住左子树的返回值，然后`root->left= left;

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
	TreeNode* insertIntoBST(TreeNode* root, int val) {
		if (root == nullptr) {
			return new TreeNode(val);
		}
		if (val > root->val) {//向右走
            TreeNode* right=insertIntoBST(root->right,val);//添加val后的右子树
            root->right=right;//考虑到原来右子树为空，添加了val的情况

		}
		else if (val < root->val) {//向左走
			TreeNode* left=insertIntoBST(root->left,val);
            root->left=left;
		}
		return root;
	}
};

迭代写法1，完全是按照递归逻辑写的，其实迭代写法还是比较容易理解的

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
	TreeNode* insertIntoBST(TreeNode* root, int val) {
        if (root == nullptr) {
			return new TreeNode(val);
		}
		TreeNode* node = root;
		while (1) {
			if (val > node->val) {//往右走
				if (node->right != nullptr) {//不为空，说明还有往右走的路
					node = node->right;
				}
				else {//为空，说明到了该插入的位置了
					node->right = new TreeNode(val);
                    break;//此时插入结束，退出循环
				}
			}
			else if (val < node->val) {
				if (node->left != nullptr) {
					node = node->left;
				}
				else {
					node->left = new TreeNode(val);
                    break;
				}

			}
		}
		return root;
	}
};

迭代写法2 ，循环找到插入的位置，用pre记录它的父节点
左右子树赋值的操作写在了循环外面，整体逻辑还是没变。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
	TreeNode* insertIntoBST(TreeNode* root, int val) {
		if (root == nullptr) {
			return new TreeNode(val);
		}
		TreeNode* node = root;
		TreeNode* pre = nullptr;//父节点
		while (node != nullptr) {
			if (val > node->val) {//往右走
				pre = node;
				node = node->right;
			}
			else if (val < node->val) {
				pre = node;
				node = node->left;
			}
		}
		if (pre != nullptr && val > pre->val) {//在pre右边插入
			pre->right = new TreeNode(val);
		}
		else if (pre != nullptr && val < pre->val) {//在pre左边插入
			pre->left = new TreeNode(val);
		}
		return root;
	}
};

450. 删除二叉搜索树中的节点

删除结点有点麻烦，要考虑到各种情况

空树删除后的根结点当然还是空树
如果删除的结点是叶子结点，删除后的根结点也是空树
如果删除的结点左子树不为空，右子树为空，删除后的根结点是删除结点的左结点
如果删除的结点左子树为空，右子树不为空，删除后的根结点是删除结点的右结点
如果删除结点的左右子树都不为空，这种情况比较复杂，画图来看一下
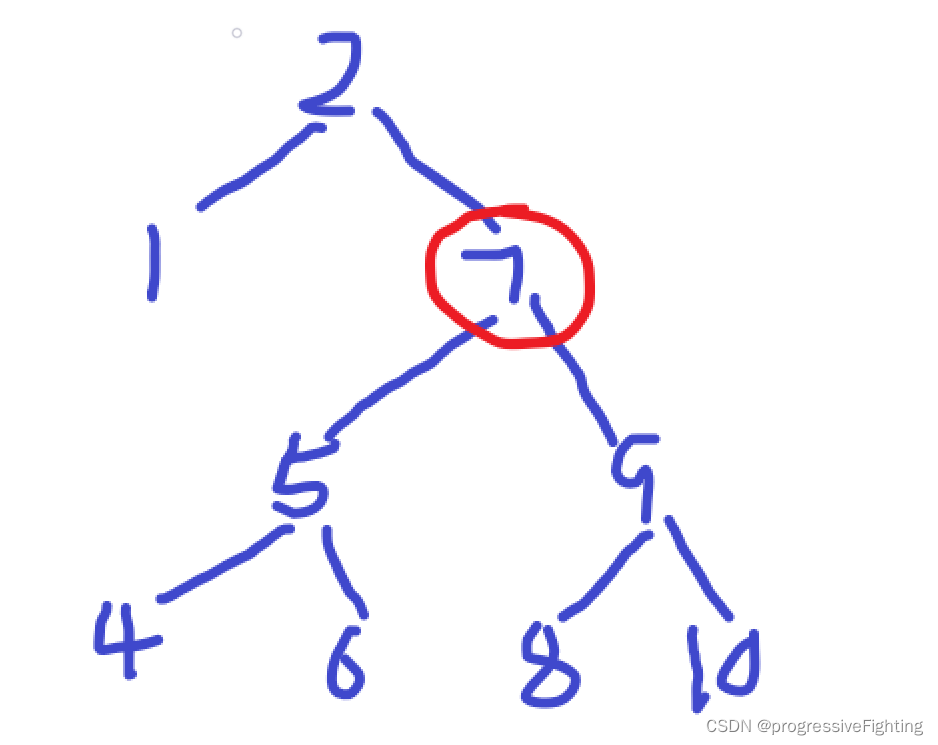
给出如下的树，要删除结点7

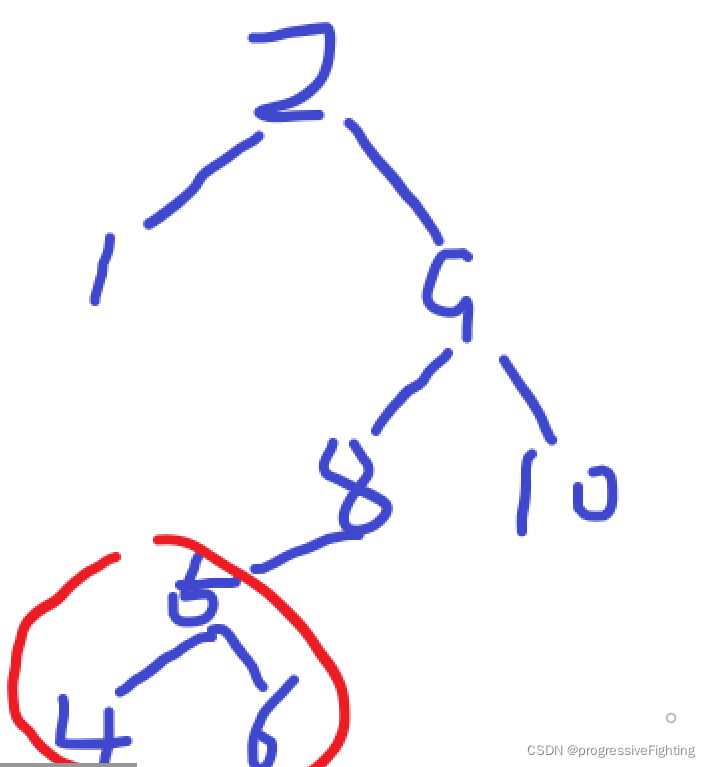
删除后的树

可以看到删除后的根结点是7的右结点，而7的左子树移动到了8的左子树上
知道了这些情况就好写递归了

参数：root，key
返回值：删除后的根结点
终止条件：空树返回空
本层递归：如果key > root->val，说明删除结点在root的右子树上，然后接住右子树删除后的根结点，然后更新root->right的值
同理如果key < root->val，说明删除结点在root的左子树上，然后接住左子树删除后的根结点，然后更新root->left的
如果key == root->val，说明找到了要删除的结点，判断是上面的哪一种情况，最后返回删除后的根结点

这道题可以说是训练递归的好题了，只有考虑到各种情况才可以跑通。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if (root == nullptr) {
            return nullptr;
        }

        if (key > root->val) {//删除点在root的右子树上
            TreeNode* newRoot = deleteNode(root->right, key);//接住删除后根结点
            root->right = newRoot;//root指向新的右子树
            return root;
        }
        else if (key < root->val) {//删除点在root的左子树上

            TreeNode* newRoot = deleteNode(root->left, key);
            root->left = newRoot;
            return root;
        }
        else {//root就是要删除的结点
            if (root->left == nullptr && root->right == nullptr) {//root是叶子结点

                delete root;//释放root
                return nullptr;//返回删除后的根结点
            }
            else if (root->left != nullptr && root->right == nullptr) {//root左子树不空，右子树为空，删除后的根结点就是root->left
                TreeNode* newRoot = root->left;//临时保存一下删除后的根结点
                delete root;
                return newRoot;
            }
            else if (root->left == nullptr && root->right != nullptr) {//root左子树为空，右子树不为空，删除后的根结点就是root->right
                TreeNode* newRoot = root->right;
                delete root;
                return newRoot;
            }
            else {//root左右子树都不空
                TreeNode* cur = root->right;
                while (cur->left != nullptr) {//找到root的右子树中最左边的叶子结点，这个叶子结点的左结点就是root的左结点，删除后的根结点就是root->right
                    cur = cur->left;
                }
                cur->left = root->left;//root的左子树转移到root的右子树中最左边的叶子结点的左结点上


                TreeNode* newRoot = root->right;
                delete root;
                return newRoot;
            }
        }

    }
};

669. 修剪二叉搜索树

要搜索整棵树，但也是有条件的搜索，如果当前点的值小于low，那么左子树的全部要剪掉，只能在右子树找第一个符合条件的点，这个点就是当前树的根结点。如果当前点的值大于high，那么右子树全部剪掉，只能在左子树找第一个符合条件的点。

参数：root，low，high
返回值：修剪后的根结点
终止条件：root为空直接返回空
本层递归：如果当前点的值小于low，往右子树找符合条件的点，这个点就是当前树修剪后的根结点，然后直接返回
如果当前点的值大于high，往左子树找符合条件的点，这个点就是当前树修剪后的根结点，然后直接返回。
如果当前点符合条件，就分别左右遍历树，然后接住左右子树的返回值来更新当前树的left和right。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
	TreeNode* trimBST(TreeNode* root, int low, int high) {
		if (root == nullptr)return nullptr;
		if (root->val < low) {//往右子树找符合条件的第一个结点
			TreeNode* right = trimBST(root->right, low, high);//root小于low，所以左子树的所有点也都小于low，可能符合条件的点只能在右子树上

			return right;
		}
		if (root->val > high) {//往左子树找符合条件的第一个结点
			TreeNode* left = trimBST(root->left, low, high);
			return left;
		}
		root->left = trimBST(root->left, low, high);
		root->right = trimBST(root->right, low, high);
		return root;
	}
};

108. 将有序数组转换为二叉搜索树

这道题和之前做过的构造二叉树还挺像的
每次选择中间的元素构造根结点保证了平衡二叉树
数组是有序的并且是递增排序的，中间元素的左边都小，右边都大，正好符合搜索二叉树的性质。
按这种规则构造出的二叉树一定是二叉平衡搜索树。
需要注意的是如果数组大小为偶数，中间的两个元素选哪个都是对的，所以才会产生多个答案。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* travel(vector<int>& nums,int l,int r){
        if(l>r){
            return nullptr;
        }
        int mid=l+(r-l)/2;//每次选中间的元素，可以保证平衡二叉树，又因为数组是有序的，所以也能保证平衡二叉树
        TreeNode* root=new TreeNode(nums[mid]);
        root->left=travel(nums,l,mid-1);
        root->right=travel(nums,mid+1,r);
        return root;
    }
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return travel(nums,0,nums.size()-1);
    }
};

538. 把二叉搜索树转换为累加树

其实右中左遍历就好了，最右边的叶子结点一定是最大的，他的值还是他本身，然后他的父节点就是他的右结点的值+他的值。
准备一个变量存累计的值，遍历中改变结点的值

参数：根结点
不需要返回值
终止条件：root为空终止
本层递归：先搜索右边的数，处理中间结点，在搜索左边的数

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int val=0;//累计值
    void travel(TreeNode* root){
        if(root==nullptr)return ;
        travel(root->right);
        val+=root->val;
        root->val=val;
        travel(root->left);
        
    }
    TreeNode* convertBST(TreeNode* root) {
        travel(root);
        return root;
    }
};

前指针写法

class Solution {
public:
    TreeNode* pre=nullptr;//前指针
    void travel(TreeNode* root){
        if(root==nullptr)return ;
        travel(root->right);
        if(pre!=nullptr){//如果为空，说明root是最右边的叶子结点，因为pre初始就是nullptr嘛
            root->val+=pre->val;
        }
        pre=root;
        travel(root->left);
        
    }
    TreeNode* convertBST(TreeNode* root) {
        travel(root);
        return root;
    }
};

迭代写法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* convertBST(TreeNode* root) {
        stack<TreeNode*>st;
        int val=0;//累加值
        if(root==nullptr)return root;
        st.push(root);
        while(!st.empty()){
            TreeNode* node=st.top();
            st.pop();
            if(node!=nullptr){
                if(node->left!=nullptr)st.push(node->left);
                st.push(node);
                st.push(nullptr);
                if(node->right!=nullptr)st.push(node->right);
            }
            else{
                node=st.top();
                st.pop();
                node->val+=val;
                val=node->val;//更新累加值
            }
        }
        return root;
    }
};

总结

二叉树相关的题目确实很多，但刷完这些基础题目确定收获挺多，总结一下吧！

二叉树的核心就是几大遍历方式，既有递归形式的又有迭代形式的。像翻转二叉树就是层序遍历的应用。
二叉树的题目基本上可以通过递归解决，因为二叉树的结构是符合递归的结构的。二叉树递归的参数不一定总是root，像对称二叉树就是要左子树的根结点和右子树的根结点，需要具体情况具体分析。
刷掉了对称二叉树，另一棵树的子树也可以用对称二叉树的套路来做，不是子树嘛，子树要么是他本身（判相等），要么是左子树的子树或者右子树的子树（递归），其实是两个递归。
求完全二叉树结点个数可不要忘了满二叉树的性质，从第一层到此底层就是满二叉树，人家是有专门公式来算结点个数的，不要傻乎乎的遍历整棵树了，别看了，说的就是我。左移一位是2的平和。
在判断平衡二叉树那里提出重要思想即需要什么造什么。
如果要搜索整棵树，其实是不需要返回值的，但也有例外，比如找最近公共祖先要在整棵树上找，由于要根据左右子树的返回值来判断，所以依然需要返回值。递归的终止条件不一定是root为空，就比如搜索树的路径，其实找到叶子结点就应该结束了。如果终止条件不是root为空，递归中要避免空节点出现。总结一下就是和路径有关的终止条件定为叶子结点就可以了。
一般求什么，返回值就是什么。特殊情况就需要造了，比如判断平衡二叉树、找最下角的值。
判断叶子结点可以通过左右孩子来判别，那么判断左叶子呢？只能通过他的父节点来判，见左叶子之和。
计算二叉搜索树的众数、最值想到前结点pre法。

【算法笔记】二叉树应用

前言

例题

总结

悦读