The Hopfield net as a distribution
The Helmholtz Free Energy of a System
-
At any time, the probability of finding the system in state s s s at temperature T T T is P T ( s ) P_T(s) PT(s)
-
At each state it has a potential energy E s E_s Es
-
The internal energy of the system, representing its capacity to do work, is the average
- U T = ∑ S P T ( s ) E S U_{T}=\sum_{S} P_{T}(s) E_{S} UT=S∑PT(s)ES
-
The capacity to do work is counteracted by the internal disorder of the system, i.e. its entropy
- H T = − ∑ S P T ( s ) log P T ( s ) H_{T}=-\sum_{S} P_{T}(s) \log P_{T}(s) HT=−S∑PT(s)logPT(s)
-
The Helmholtz free energy of the system measures the useful work derivable from it and combines the two terms
- F T = U T + k T H T F_{T}=U_{T}+k T H_{T} FT=UT+kTHT
- = ∑ S P T ( s ) E S − k T ∑ S P T ( s ) log P T ( s ) =\sum_{S} P_{T}(s) E_{S}-k T \sum_{S} P_{T}(s) \log P_{T}(s) =S∑PT(s)ES−kTS∑PT(s)logPT(s)
-
The probability distribution of the states at steady state is known as the Boltzmann distribution
-
Minimizing this w.r.t P T ( s ) P_T(s) PT(s), we get
-
P T ( s ) = 1 Z exp ( − E S k T ) P_{T}(s)=\frac{1}{Z} \exp \left(\frac{-E_{S}}{k T}\right) PT(s)=Z1exp(kT−ES)
-
Z Z Z is a normalizing constant
-
Hopfield net as a distribution
- E ( S ) = − ∑ i < j w i j s i s j − b i s i E(S)=-\sum_{i<j} w_{i j} s_{i} s_{j}-b_{i} s_{i} E(S)=−∑i<jwijsisj−bisi
- P ( S ) = exp ( − E ( S ) ) ∑ S ′ exp ( − E ( S ′ ) ) P(S)=\frac{\exp (-E(S))}{\sum_{S^{\prime}} \exp \left(-E\left(S^{\prime}\right)\right)} P(S)=∑S′exp(−E(S′))exp(−E(S))
- The stochastic Hopfield network models a probability distribution over states
- It is a generative model: generates states according to P ( S ) P(S) P(S)
The field at a single node
-
Let’s take one node as example
-
Let S S S and S ′ S^\prime S′ be the states with the +1 and -1 states
- P ( S ) = P ( s i = 1 ∣ s j ≠ i ) P ( s j ≠ i ) P(S)=P\left(s_{i}=1 \mid s_{j \neq i}\right) P\left(s_{j \neq i}\right) P(S)=P(si=1∣sj=i)P(sj=i)
- P ( S ′ ) = P ( s i = − 1 ∣ s j ≠ i ) P ( s j ≠ i ) P\left(S^{\prime}\right)=P\left(s_{i}=-1 \mid s_{j \neq i}\right) P\left(s_{j \neq i}\right) P(S′)=P(si=−1∣sj=i)P(sj=i)
- log P ( S ) − log P ( S ′ ) = log P ( s i = 1 ∣ s j ≠ i ) − log P ( s i = − 1 ∣ s j ≠ i ) \log P(S)-\log P\left(S^{\prime}\right)=\log P\left(s_{i}=1 \mid s_{j \neq i}\right)-\log P\left(s_{i}=-1 \mid s_{j \neq i}\right) logP(S)−logP(S′)=logP(si=1∣sj=i)−logP(si=−1∣sj=i)
- log P ( S ) − log P ( S ′ ) = log P ( s i = 1 ∣ s j ≠ i ) 1 − P ( s i = 1 ∣ s j ≠ i ) \log P(S)-\log P\left(S^{\prime}\right)=\log \frac{P\left(s_{i}=1 \mid s_{j \neq i}\right)}{1-P\left(s_{i}=1 \mid s_{j \neq i}\right)} logP(S)−logP(S′)=log1−P(si=1∣sj=i)P(si=1∣sj=i)
-
log P ( S ) = − E ( S ) + C \log P(S)=-E(S)+C logP(S)=−E(S)+C
- E ( S ) = − 1 2 ( E not i + ∑ j ≠ i w i j s j + b i ) E(S)=-\frac{1}{2}\left(E_{\text {not } i}+\sum_{j \neq i} w_{i j} s_{j}+b_{i}\right) E(S)=−21(Enot i+∑j=iwijsj+bi)
- E ( S ′ ) = − 1 2 ( E not i − ∑ j ≠ i w i j s j − b i ) E\left(S^{\prime}\right)=-\frac{1}{2}\left(E_{\text {not } i}-\sum_{j \neq i} w_{i j} s_{j}-b_{i}\right) E(S′)=−21(Enot i−∑j=iwijsj−bi)
-
log P ( S ) − log P ( S ′ ) = E ( S ′ ) − E ( S ) = ∑ j ≠ i w i j S j + b i \log P(S)-\log P\left(S^{\prime}\right)=E\left(S^{\prime}\right)-E(S)=\sum_{j \neq i} w_{i j} S_{j}+b_{i} logP(S)−logP(S′)=E(S′)−E(S)=∑j=iwijSj+bi
-
log ( P ( s i = 1 ∣ s j ≠ i ) 1 − P ( s i = 1 ∣ s j ≠ i ) ) = ∑ j ≠ i w i j s j + b i \log \left(\frac{P\left(s_{i}=1 \mid s_{j \neq i}\right)}{1-P\left(s_{i}=1 \mid s_{j \neq i}\right)}\right)=\sum_{j \neq i} w_{i j} s_{j}+b_{i} log(1−P(si=1∣sj=i)P(si=1∣sj=i))=∑j=iwijsj+bi
-
P ( s i = 1 ∣ s j ≠ i ) = 1 1 + e − ( ∑ j ≠ i w i j s j + b i ) P\left(s_{i}=1 \mid s_{j \neq i}\right)=\frac{1}{1+e^{-\left(\sum_{j \neq i} w_{i j} s_{j}+b_{i}\right)}} P(si=1∣sj=i)=1+e−(∑j=iwijsj+bi)1
-
-
The probability of any node taking value 1 given other node values is a logistic
Redefining the network
- Redefine a regular Hopfield net as a stochastic system
- Each neuron is now a stochastic unit with a binary state
s
i
s_i
si, which can take value 0 or 1 with a probability that depends on the local field
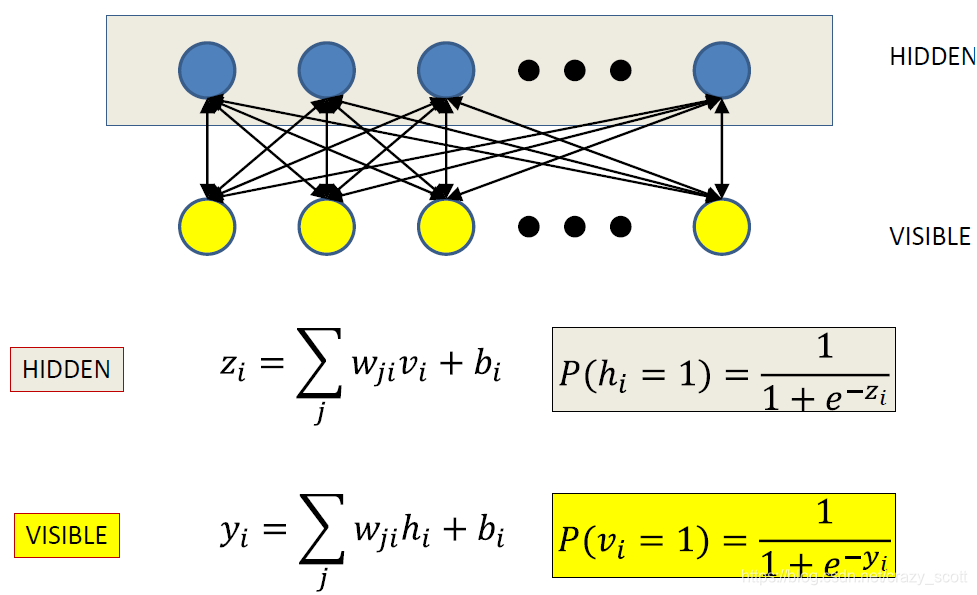
- z i = ∑ j w i j s j + b i z_{i}=\sum_{j} w_{i j} s_{j}+b_{i} zi=∑jwijsj+bi
- P ( s i = 1 ∣ s j ≠ i ) = 1 1 + e − z i P\left(s_{i}=1 \mid s_{j \neq i}\right)=\frac{1}{1+e^{-z_{i}}} P(si=1∣sj=i)=1+e−zi1
- Note
- The Hopfield net is a probability distribution over binary sequences (Boltzmann distribution)
- The conditional distribution of individual bits in the sequence is a logistic
- The evolution of the Hopfield net can be made stochastic
- Instead of deterministically responding to the sign of the local field, each neuron responds probabilistically
- Recall patterns
The Boltzmann Machine
- The entire model can be viewed as a generative model
- Has a probability of producing any binary vector
y
y
y
- E ( y ) = − 1 2 y T W y E(\mathbf{y})=-\frac{1}{2} \mathbf{y}^{T} \mathbf{W} \mathbf{y} E(y)=−21yTWy
- P ( y ) = Cexp ( − E ( y ) T ) P(\mathbf{y})=\operatorname{Cexp}\left(-\frac{E(\mathbf{y})}{T}\right) P(y)=Cexp(−TE(y))
- Training a Hopfield net: Must learn weights to “remember” target states and “dislike” other states
- Must learn weights to assign a desired probability distribution to states
- Just maximize likelihood
Maximum Likelihood Training
-
log ( P ( S ) ) = ( ∑ i < j w i j s i s j ) − log ( ∑ S ′ exp ( ∑ i < j w i j s i ′ s j ′ ) ) \log (P(S))=\left(\sum_{i<j} w_{i j} s_{i} s_{j}\right)-\log \left(\sum_{S^{\prime}} \exp \left(\sum_{i<j} w_{i j} s_{i}^{\prime} s_{j}^{\prime}\right)\right) log(P(S))=(∑i<jwijsisj)−log(∑S′exp(∑i<jwijsi′sj′))
-
L = 1 N ∑ S ∈ S log ( P ( S ) ) = 1 N ∑ S ( ∑ i < j w i j s i s j ) − log ( ∑ S ′ exp ( ∑ i < j w i j s i ′ s j ′ ) ) \mathcal{L}=\frac{1}{N} \sum_{S \in \mathbf{S}} \log (P(S)) =\frac{1}{N} \sum_{S}\left(\sum_{i<j} w_{i j} s_{i} s_{j}\right)-\log \left(\sum_{S^{\prime}} \exp \left(\sum_{i<j} w_{i j} s_{i}^{\prime} s_{j}^{\prime}\right)\right) L=N1∑S∈Slog(P(S))=N1∑S(∑i<jwijsisj)−log(∑S′exp(∑i<jwijsi′sj′))
-
Second term derivation
- d log ( ∑ S ′ exp ( ∑ i < j w i j s i ′ s j ′ ) ) d w i j = ∑ S ′ exp ( ∑ i < j w i j s i ′ s j ′ ) ∑ S ′ exp ( ∑ i < j w i j s i ′ ′ s j ′ ) s i ′ s j ′ \frac{d \log \left(\sum_{S^{\prime}} \exp \left(\sum_{i<j} w_{i j} s_{i}^{\prime} s_{j}^{\prime}\right)\right)}{d w_{i j}}=\sum_{S^{\prime}} \frac{\exp \left(\sum_{i<j} w_{i j} s_{i}^{\prime} s_{j}^{\prime}\right)}{\sum_{S^{\prime}} \exp \left(\sum_{i<j} w_{i j} s_{i}^{\prime \prime} s_{j}^{\prime}\right)} s_{i}^{\prime} s_{j}^{\prime} dwijdlog(∑S′exp(∑i<jwijsi′sj′))=∑S′∑S′exp(∑i<jwijsi′′sj′)exp(∑i<jwijsi′sj′)si′sj′
- d log ( ∑ S ′ exp ( ∑ i < j w i j s i ′ s j ′ ) ) d w i j = ∑ S ′ P ( S ′ ) s i ′ s j ′ \frac{d \log \left(\sum_{S^{\prime}} \exp \left(\sum_{i<j} w_{i j} s_{i}^{\prime} s_{j}^{\prime}\right)\right)}{d w_{i j}}=\sum_{S_{\prime}} P\left(S^{\prime}\right) s_{i}^{\prime} s_{j}^{\prime} dwijdlog(∑S′exp(∑i<jwijsi′sj′))=∑S′P(S′)si′sj′
- The second term is simply the expected value of s i S j s_iS_j siSj, over all possible values of the state
- We cannot compute it exhaustively, but we can compute it by sampling!
-
Overall gradient ascent rule
- w i j = w i j + η d ⟨ log ( P ( S ) ) ⟩ d w i j w_{i j}=w_{i j}+\eta \frac{d\langle\log (P(\mathbf{S}))\rangle}{d w_{i j}} wij=wij+ηdwijd⟨log(P(S))⟩
-
Overall Training
- Initialize weights
- Let the network run to obtain simulated state samples
- Compute gradient and update weights
- Iterate
-
Note the similarity to the update rule for the Hopfield network
- The only difference is how we got the samples
Adding Capacity
-
Visible neurons
- The neurons that store the actual patterns of interest
-
Hidden neurons
- The neurons that only serve to increase the capacity but whose actual values are not important
-
We could have multiple hidden patterns coupled with any visible pattern
- These would be multiple stored patterns that all give the same visible output
-
We are interested in the marginal probabilities over visible bits
- S = ( V , H ) S=(V,H) S=(V,H)
- P ( S ) = exp ( − E ( S ) ) ∑ S ′ exp ( − E ( S ′ ) ) P(S)=\frac{\exp (-E(S))}{\sum_{S^{\prime}} \exp \left(-E\left(S^{\prime}\right)\right)} P(S)=∑S′exp(−E(S′))exp(−E(S))
- P ( S ) = P ( V , H ) P(S) = P(V,H) P(S)=P(V,H)
- P ( V ) = ∑ H P ( S ) P(V)=\sum_{H} P(S) P(V)=∑HP(S)
-
Train to maximize probability of desired patterns of visible bits
- E ( S ) = − ∑ i < j w i j s i s j E(S)=-\sum_{i<j} w_{i j} s_{i} s_{j} E(S)=−∑i<jwijsisj
- P ( S ) = exp ( ∑ i < j w i j s i s j ) ∑ S ′ exp ( ∑ i < j w i j s i ′ s j ′ ) P(S)=\frac{\exp \left(\sum_{i<j} w_{i j} s_{i} s_{j}\right)}{\sum_{S^{\prime}} \exp \left(\sum_{i<j} w_{i j} s_{i}^{\prime} s_{j}^{\prime}\right)} P(S)=∑S′exp(∑i<jwijsi′sj′)exp(∑i<jwijsisj)
- P ( V ) = ∑ H exp ( ∑ i < j w i j s i s j ) ∑ S ′ exp ( ∑ i < j w i j s i ′ s j ′ ) P(V)=\sum_{H} \frac{\exp \left(\sum_{i<j} w_{i j} s_{i} s_{j}\right)}{\sum_{S^{\prime}} \exp \left(\sum_{i<j} w_{i j} s_{i}^{\prime} s_{j}^{\prime}\right)} P(V)=∑H∑S′exp(∑i<jwijsi′sj′)exp(∑i<jwijsisj)
-
Maximum Likelihood Training
log ( P ( V ) ) = log ( ∑ H exp ( ∑ i < j w i j s i s j ) ) − log ( ∑ S ′ exp ( ∑ i < j w i j s i ′ s j ′ ) ) \log (P(V))=\log \left(\sum_{H} \exp \left(\sum_{i<j} w_{i j} s_{i} s_{j}\right)\right)-\log \left(\sum_{S_{\prime}} \exp \left(\sum_{i<j} w_{i j} s_{i}^{\prime} s_{j}^{\prime}\right)\right) log(P(V))=log(H∑exp(i<j∑wijsisj))−log(S′∑exp(i<j∑wijsi′sj′))
L = 1 N ∑ V ∈ V log ( P ( V ) ) \mathcal{L}=\frac{1}{N} \sum_{V \in \mathbf{V}} \log (P(V)) L=N1V∈V∑log(P(V))
d L d w i j = 1 N ∑ V ∈ V ∑ H P ( S ∣ V ) s i s j − ∑ S ! P ( S ′ ) s i ′ s j ′ \frac{d \mathcal{L}}{d w_{i j}}=\frac{1}{N} \sum_{V \in \mathbf{V}} \sum_{H} P(S \mid V) s_{i} s_{j}-\sum_{S !} P\left(S^{\prime}\right) s_{i}^{\prime} s_{j}^{\prime} dwijdL=N1V∈V∑H∑P(S∣V)sisj−S!∑P(S′)si′sj′ -
∑ H P ( S ∣ V ) s i s j ≈ 1 K ∑ H ∈ H s i m u l s i S j \sum_{H} P(S \mid V) s_{i} s_{j} \approx \frac{1}{K} \sum_{H \in \mathbf{H}_{s i m u l}} s_{i} S_{j} ∑HP(S∣V)sisj≈K1∑H∈HsimulsiSj
-
Computed as the average sampled hidden state with the visible bits fixed
-
∑ S ′ P ( S ′ ) s i ′ s j ′ ≈ 1 M ∑ S i ∈ S s i m u l s i ′ S j ′ \sum_{S^{\prime}} P\left(S^{\prime}\right) s_{i}^{\prime} s_{j}^{\prime} \approx \frac{1}{M} \sum_{S_{i} \in \mathbf{S}_{s i m u l}} s_{i}^{\prime} S_{j}^{\prime} ∑S′P(S′)si′sj′≈M1∑Si∈Ssimulsi′Sj′
- Computed as the average of sampled states when the network is running “freely”
Training
Step1
- For each training pattern
V
i
V_i
Vi
- Fix the visible units to V i V_i Vi
- Let the hidden neurons evolve from a random initial point to generate H i H_i Hi
- Generate S i = [ V i , H i ] S_i = [V_i,H_i] Si=[Vi,Hi]
- Repeat K times to generate synthetic training
S = { S 1 , 1 , S 1 , 2 , … , S 1 K , S 2 , 1 , … , S N , K } \mathbf{S}=\{S_{1,1}, S_{1,2}, \ldots, S_{1 K}, S_{2,1}, \ldots, S_{N, K}\} S={S1,1,S1,2,…,S1K,S2,1,…,SN,K}
Step2
- Now unclamp the visible units and let the entire network evolve several times to generate
S s i m u l = S _ s i m u l , 1 , S _ s i m u l , 2 , … , S _ s i m u l , M \mathbf{S}_{simul}=S\_{simul, 1}, S\_{simul, 2}, \ldots, S\_{simul, M} Ssimul=S_simul,1,S_simul,2,…,S_simul,M
Gradients
d
⟨
log
(
P
(
S
)
)
⟩
d
w
i
j
=
1
N
K
∑
S
s
i
s
j
−
1
M
∑
S
i
∈
S
simul
s
i
′
s
j
′
\frac{d\langle\log (P(\mathbf{S}))\rangle}{d w_{i j}}=\frac{1}{N K} \sum_{\boldsymbol{S}} s_{i} s_{j}-\frac{1}{M} \sum_{S_{i} \in \mathbf{S}_{\text {simul }}} s_{i}^{\prime} s_{j}^{\prime}
dwijd⟨log(P(S))⟩=NK1S∑sisj−M1Si∈Ssimul ∑si′sj′
w i j = w i j − η d ⟨ log ( P ( S ) ) ⟩ d w i j w_{i j}=w_{i j}-\eta \frac{d\langle\log (P(\mathbf{S}))\rangle}{d w_{i j}} wij=wij−ηdwijd⟨log(P(S))⟩
- Gradients are computed as before, except that the first term is now computed over the expanded training data
Issues
- Training takes for ever
- Doesn’t really work for large problems
- A small number of training instances over a small number of bits
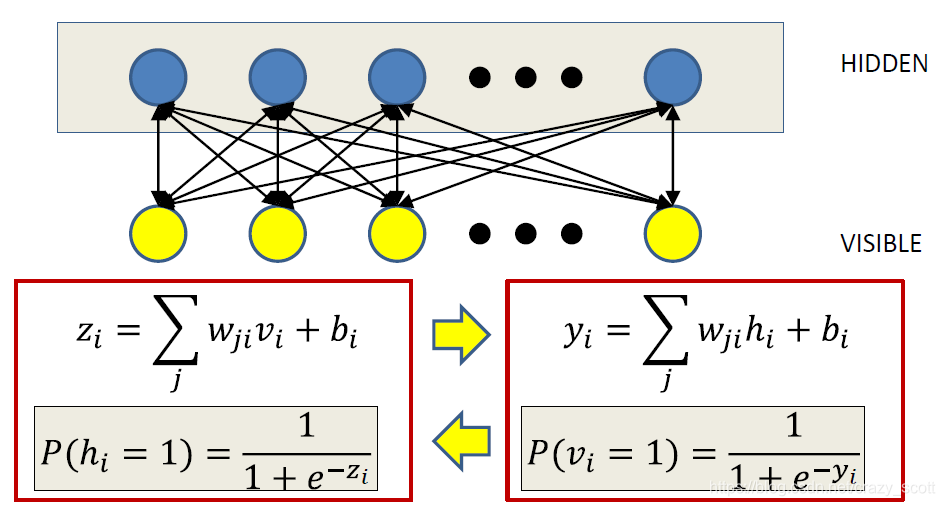
Restricted Boltzmann Machines
- Partition visible and hidden units
- Visible units ONLY talk to hidden units
- Hidden units ONLY talk to visible units
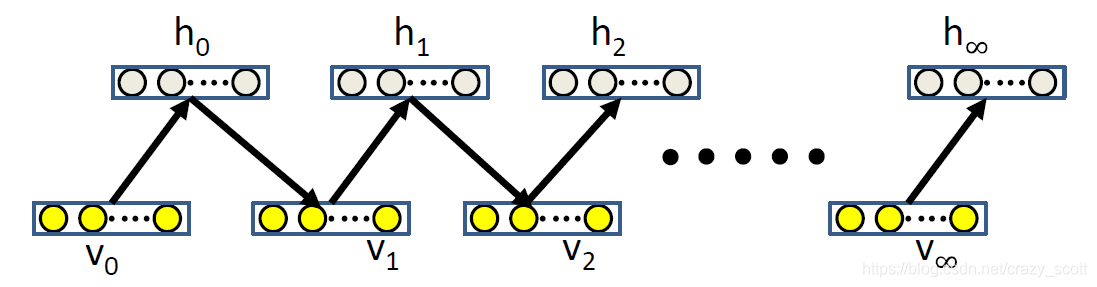
Training
Step1
- For each sample
- Anchor visible units
- Sample from hidden units
- No looping!!
Step2
- Now unclamp the visible units and let the entire network evolve several times to generate
S s i m u l = S _ s i m u l , 1 , S _ s i m u l , 2 , … , S _ s i m u l , M \mathbf{S}_{simul}=S\_{simul, 1}, S\_{simul, 2}, \ldots, S\_{simul, M} Ssimul=S_simul,1,S_simul,2,…,S_simul,M
- For each sample
- Initialize V 0 V_0 V0 (visible) to training instance value
- Iteratively generate hidden and visible units
- Gradient
∂ log p ( v ) ∂ w i j = < v i h j > 0 − < v i h j > ∞ \frac{\partial \log p(v)}{\partial w_{i j}}=<v_{i} h_{j}>^{0}-<v_{i} h_{j}>^{\infty} ∂wij∂logp(v)=<vihj>0−<vihj>∞
A Shortcut: Contrastive Divergence
- Recall: Raise the neighborhood of each target memory
- Sufficient to run one iteration to give a good estimate of the gradient
∂ log p ( v ) ∂ w i j = < v i h j > 0 − < v i h j > 1 \frac{\partial \log p(v)}{\partial w_{i j}}=< v_{i} h_{j}>^{0}-<v_{i} h_{j}>^{1} ∂wij∂logp(v)=<vihj>0−<vihj>1