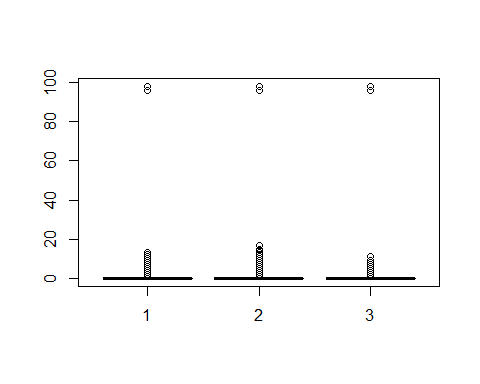信用评分
2016年1月10日
本文详细的介绍了信用评分卡的开发流程,开发语言为R语言,python版本请见:一行代码搞定信用评分模型(python)
python版实例和数据请见我的github:https://github.com/chengsong990020186/CreditScoreModel,如觉得实用就点下star,欢迎大家一起学习交流进步。
一、数据准备
1、 问题的准备
• 目标:要完成一个评分卡,通过预测某人在未来两年内将会经历财务危机的可能性来提高信用评分的效果,帮助贷款人做出最好的决策。
• 背景:
– 银行在市场经济中起到至关重要的作用。他们决定谁在什么条件下可以得到融资,并且可以创造或打破投资决策。而市场、社会,以及个人和企业都需要获得贷款。
– 信用评分算法,对默认可能性进行猜测,这是银行用来判断贷款是否应该被授予的方法。
• 准备:
– 首先是基于个人借贷的场景,确定“违约”的定义: 根据新的Basel II Capital Accord(巴塞尔二资本协议),一般逾期90天算作违约。
– 在判别指标上,选择使用历史最大违约天数。
2、数据的获取与整合
• 数据来源:数据来自Kaggle,cs-training.csv是有15万条的样本数据,下图可以看到这份数据的大致情况。下载地址 为:https://www.kaggle.com/c/GiveMeSomeCredit/data
如果下载出现问题,可以在此下载数据:http://download.csdn.net/download/csqazwsxedc/10228999
• 数据描述:数据属于个人消费类贷款,只考虑评分卡最终实施时能够使用到的数据应从如下一些方面获取数据:
– 基本属性:包括了借款人当时的年龄。
– 偿债能力:包括了借款人的月收入、负债比率。
– 信用往来:两年内35-59天逾期次数、两年内60-89天逾期次数、两年内90天或高于90天逾期的次数。
– 财产状况:包括了开放式信贷和贷款数量、不动产贷款或额度数量。
– 贷款属性:暂无。
– 其他因素:包括了借款人的家属数量(不包括本人在内)。
• 原始变量:
| 变量名 |
变量类型 |
变量描述 |
| SeriousDlqin2yrs |
Y/N |
超过90天或更糟的逾期拖欠 |
| RevolvingUtilizationOf UnsecuredLines |
percentage |
无担保放款的循环利用:除了不动产和像车贷那样除以信用额度总和的无分期付款债务的信用卡和个人信用额度总额 |
| age |
integer |
借款人当时的年龄 |
| NumberOfTime30-59DaysPastDueNotWorse |
integer |
35-59天逾期但不糟糕次数 |
| DebtRatio |
percentage |
负债比率 |
| MonthlyIncome |
real |
月收入 |
| NumberOf OpenCreditLinesAndLoans |
integer |
开放式信贷和贷款数量,开放式贷款(分期付款如汽车贷款或抵押贷款)和信贷(如信用卡)的数量 |
| NumberOfTimes90DaysLate |
integer |
90天逾期次数:借款者有90天或更高逾期的次数 |
| NumberRealEstateLoans OrLines |
integer |
不动产贷款或额度数量:抵押贷款和不动产放款包括房屋净值信贷额度 |
| NumberOfTime60-89DaysPastDueNotWorse |
integer |
60-89天逾期但不糟糕次数:借款人在在过去两年内有60-89天逾期还款但不糟糕的次数 |
| NumberOfDependents |
integer |
家属数量:不包括本人在内的家属数量 |
• 时间窗口:自变量的观察窗口为过去两年,因变量表现窗口为未来两年。
二、数据处理
首先去掉原数据中的顺序变量,即第一列的id变量。由于要预测的是SeriousDlqin2yrs变量,因此将其设为响应变量y,其他分别设为x1~x10变量。
1、缺失值分析及处理
在得到数据集后,我们需要观察数据的分布情况,因为很多的模型对缺失值敏感,因此观察是否有缺失值是其中很重要的一个步骤。在正式分析前,我们先通过图形进行对观测字段的缺失情况有一个直观的感受。
matrixplot(traindata)
md.pattern(traindata)## y x1 x2 x3 x4 x6 x7 x8 x9 x10 x5
## 120269 1 1 1 1 1 1 1 1 1 1 1 0
## 25807 1 1 1 1 1 1 1 1 1 1 0 1
## 3924 1 1 1 1 1 1 1 1 1 0 0 2
## 0 0 0 0 0 0 0 0 0 3924 29731 33655
利用matrixplot函数对缺失值部分进行可视化展示,上图中浅色表示值小,深色表示值大,而默认缺失值为红色。因此可以看到x5变量和x10变量,即MonthlyIncome变量和NumberOfDependents两个变量存在缺失值,具体确实情况可以见上表,monthlyincome列共有缺失值29731个,numberofdependents有3924个。
对于缺失值的处理方法非常多,例如基于聚类的方法,基于回归的方法,基于均值的方法,其中最简单的方法是直接移除,但是在本文中因为缺失值所占比例较高,直接移除会损失大量观测,因此并不是最合适的方法。在这里,我们使用KNN方法对缺失值进行填补。
traindata<-knnImputation(traindata,k=10,meth = "weighAvg")
2、异常值分析及处理
关于异常值的检测,这里简单介绍以下一些检测方法:
• 单变量异常值检测:在R语言中使用函数boxplot.stats()可以实现单变量检测,该函数根据返回的统计数据生成箱线图。在上述函数的返回结果中,有一个参数out,它是由异常值组成的列表。更明确的说就是里面列出了箱线图中箱须线外面的数据点。比如我们可以查看月收入分布,第一幅图为没有删除异常值的箱线图。第二幅箱线图删除异常值后,可以发现月收入主要集中分布在3000-8000之间。但是在这份分析报告中,因为我们对业务尚不熟悉,不好将大于8000的数据直接归为异常值,因此对该变量未做处理。
• 使用LOF(局部异常因子)检测异常值:LOF(局部异常因子)是一种基于密度识别异常值的算法。算法实现是:将一个点的局部密度与分布在它周围的点的密度相比较,如果前者明显的比后者小,那么这个点相对于周围的点来说就处于一个相对比较稀疏的区域,这就表明该点事一个异常值。LOF算法的缺点是它只对数值型数据有效。包‘DMwR’和包‘dprep’中的lofactor()可以计算LOF算法中的局部异常因子。
• 通过聚类检测异常值:检测异常值的另外一种方式就是聚类。先把数据聚成不同的类,选择不属于任何类的数据作为异常值。例如,基于密度的聚类DBSCAN算法的实现就是将与数据稠密区域紧密相连的数据对象划分为一个类,因此与其他对象分离的数据就会作为异常值。也可以使用K均值算法实现异常值的检测。首先通过把数据划分为k组,划分方式是选择距离各自簇中心最近的点为一组;然后计算每个对象和对应的簇中心的距离(或者相似度),并挑出拥有最大的距离的点作为异常值。
首先对于x2变量,即客户的年龄,我们可以定量分析,发现有以下值:
unique(traindata$x2)## [1] 45 40 38 30 49 74 57 39 27 51 46 76 64 78 53 43 25
## [18] 32 58 50 69 24 28 62 42 75 26 52 41 81 31 68 70 73
## [35] 29 55 35 72 60 67 36 56 37 66 83 34 44 48 61 80 47
## [52] 59 77 63 54 33 79 65 86 92 23 87 71 22 90 97 84 82
## [69] 91 89 85 88 21 93 96 99 94 95 101 98 103 102 107 105 0
## [86] 109
可以看到年龄中存在0值,显然是异常值,予以剔除。
traindata<-traindata[-which(traindata$x2==0),]
而对于x3,x7,x9三个变量,由下面的箱线图可以看出,均存在异常值,且由unique函数可以得知均存在96、98两个异常值,因此予以剔除。同时会发现剔除其中一个变量的96、98值,其他变量的96、98两个值也会相应被剔除
## [1] 2 0 1 3 4 5 7 10 6 98 12 8 9 96 13 11## [1] 0 1 3 2 5 4 98 10 9 6 7 8 15 96 11 13 14 17 12## [1] 0 1 2 5 3 98 4 6 7 8 96 11 9
其它变量占不作处理。
三、变量分析
1、单变量分析
我们可以简单地看下部分变量的分布,比如对于age变量,如下图:
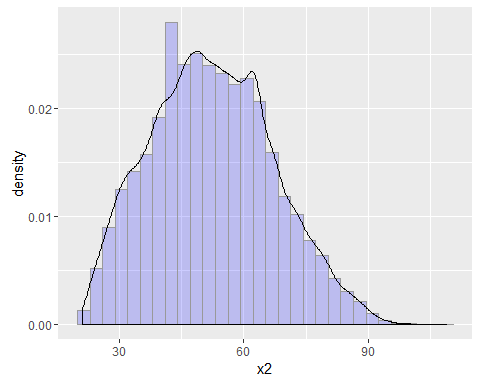
ggplot(traindata, aes(x = x2, y = ..density..)) + geom_histogram(fill = "blue", colour = "grey60", size = 0.2, alpha = 0.2) + geom_density()
可以看到年龄变量大致呈正态分布,符合统计分析的假设。再比如月收入变量,也可以做图观察观察,如下:
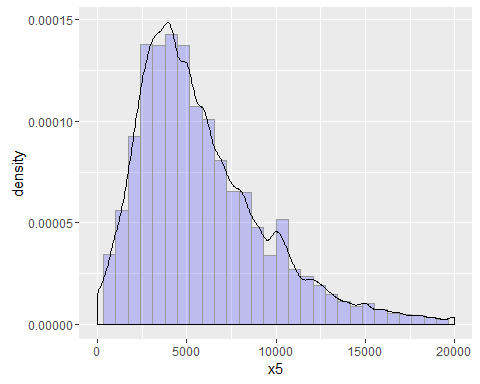
ggplot(traindata, aes(x = x5, y = ..density..)) + geom_histogram(fill = "blue", colour = "grey60", size = 0.2, alpha = 0.2) + geom_density() + xlim(1, 20000)
月收入也大致呈正态分布,符合统计分析的需要。
2、变量之间的相关性
建模之前首先得检验变量之间的相关性,如果变量之间相关性显著,会影响模型的预测效果。下面通过corrplot函数,画出各变量之间,包括响应变量与自变量的相关性。
cor1<-cor(traindata[,1:11])
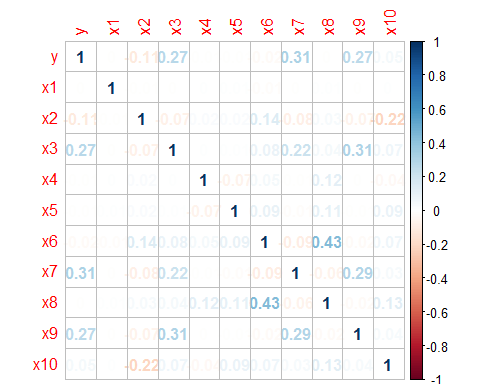
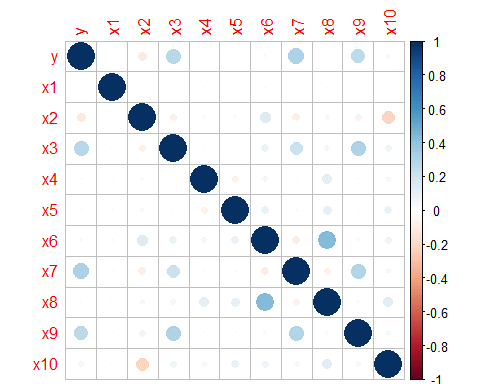
corrplot(cor1)
corrplot(cor1,method = "number")
由上图可以看出,各变量之间的相关性是非常小的。其实Logistic回归同样需要检验多重共线性问题,不过此处由于各变量之间的相关性较小,可以初步判断不存在多重共线性问题,当然我们在建模后还可以用VIF(方差膨胀因子)来检验多重共线性问题。如果存在多重共线性,即有可能存在两个变量高度相关,需要降维或剔除处理。
四、切分数据集
table(traindata$y)##
## 0 1
## 139851 9879
由上表看出,对于响应变量SeriousDlqin2yrs,存在明显的类失衡问题,SeriousDlqin2yrs等于1的观测为9879,仅为所有观测值的6.6%。因此我们需要对非平衡数据进行处理,在这里可以采用SMOTE算法,用R对稀有事件进行超级采样。
我们利用caret包中的createDataPartition(数据分割功能)函数将数据随机分成相同的两份。
set.seed(1234)
splitIndex<-createDataPartition(traindata$y,time=1,p=0.5,list=FALSE)
train<-traindata[splitIndex,]
test<-traindata[-splitIndex,]
对于分割后的训练集和测试集均有74865个数据,分类结果的平衡性如下:
prop.table(table(train$y))
##
## 0 1
## 0.93314633 0.06685367
prop.table(table(test$y)) ##
## 0 1
## 0.93489615 0.06510385
两者的分类结果是平衡的,仍然有6.6%左右的代表,我们仍然处于良好的水平。因此可以采用这份切割的数据进行建模及预测。
五、Logistic回归
Logistic回归在信用评分卡开发中起到核心作用。由于其特点,以及对自变量进行了证据权重转换(WOE),Logistic回归的结果可以直接转换为一个汇总表,即所谓的标准评分卡格式。
2、建立模型
首先利用glm函数对所有变量进行Logistic回归建模,模型如下
fit<-glm(y~.,train,family = "binomial")
summary(fit)##
## Call:
## glm(formula = y ~ ., family = "binomial", data = train)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -4.6144 -0.3399 -0.2772 -0.2240 3.6997
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.812e+00 6.