一、题目
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 1:
输入:heights = [2,1,5,6,2,3] 输出:10 解释:最大的矩形为图中红色区域,面积为 10
示例 2:
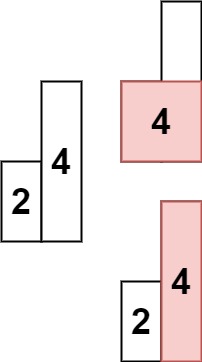
输入: heights = [2,4] 输出: 4
提示:
1 <= heights.length <=1050 <= heights[i] <= 104
二、代码
class Solution {
public int largestRectangleArea(int[] heights) {
// 过滤无效参数
if (heights == null || heights.length == 0) {
return 0;
}
int n = heights.length;
// 创建单调栈
int[] stack = new int [n];
int top = -1;
int max = Integer.MIN_VALUE;
// 遍历数组,将每个数组添加进单调栈中
// 找到每个位置左右能扩大的最大范围,就是距离当前位置的长方形最近的并且高度小于它的长方形,在这两个高度小于它的长方形之间的全部长方形,都是可以扩张到形成大长方形的
for (int i = 0; i < n; i++) {
while (top != -1 && heights[stack[top]] >= heights[i]) {
int index = stack[top--];
// 形成的长方形高度都是固定的,都是heights[index],也就是从栈中弹出的高度
max = Math.max(max, top == -1 ? heights[index] * i : heights[index] * (i - stack[top] - 1));
}
stack[++top] = i;
}
// 单独处理单调栈中剩下的长方形
while (top != -1) {
int index = stack[top--];
max = Math.max(max, top == -1 ? heights[index] * n : heights[index] * (n - stack[top] - 1));
}
return max;
}
}三、解题思路
最终求的长方形,一定以某一个值为高,然后能扩出最大的宽度来(扩张到离自己最近的并且高度比自己小的直方图为止)。这样能求出来以每一个高度能扩出来的最大宽度是多少,然后就去从这些结果里面取一个面子最大的(宽 * 高)即可。整个题和之前写的那道题基本是一样的,这里就能看到模型转换的重要性,我们把一个看似不相干的题目转换成了从某个点开始向左右扩,按照某种规则扩到最大,然后在所有结果中求最值的题目,这样就可以用单调栈来求解了。