4、Vanilla Graph Neural Networks（原始图神经网络）

在本节中，我们描述了Scarselli et al. [2009] 文章中提出的Vanilla GNN。此外，我们同时列出了Vanilla GNN在表示能力和训练效率方面的局限性。在本章之后，我们将讨论Vanilla GNN的集中变体。

4.1、 Introduction

GNN的概念最早是Gori et al. [2005], Scarselli et al. [2004, 2009]. 中提出的。为了简单起见，我们将讨论Scarselli et al. [2004, 2009]. 中提出的模型，该模型旨在扩展现有的神经网络来处理图结构数据。

一个节点自然由其特征及图中相关的节点定义。GNN的目标是为每一个节点学习一个状态embedding ${\mathbf{h}}_v\in {\mathbb{R}}^s$，该状态对领域的信息进行了嵌入编码。状态embedding ${\mathbf{h}}_v$用于产生一个输出${\mathbf{o}}_v$，如预测节点标签的分布。

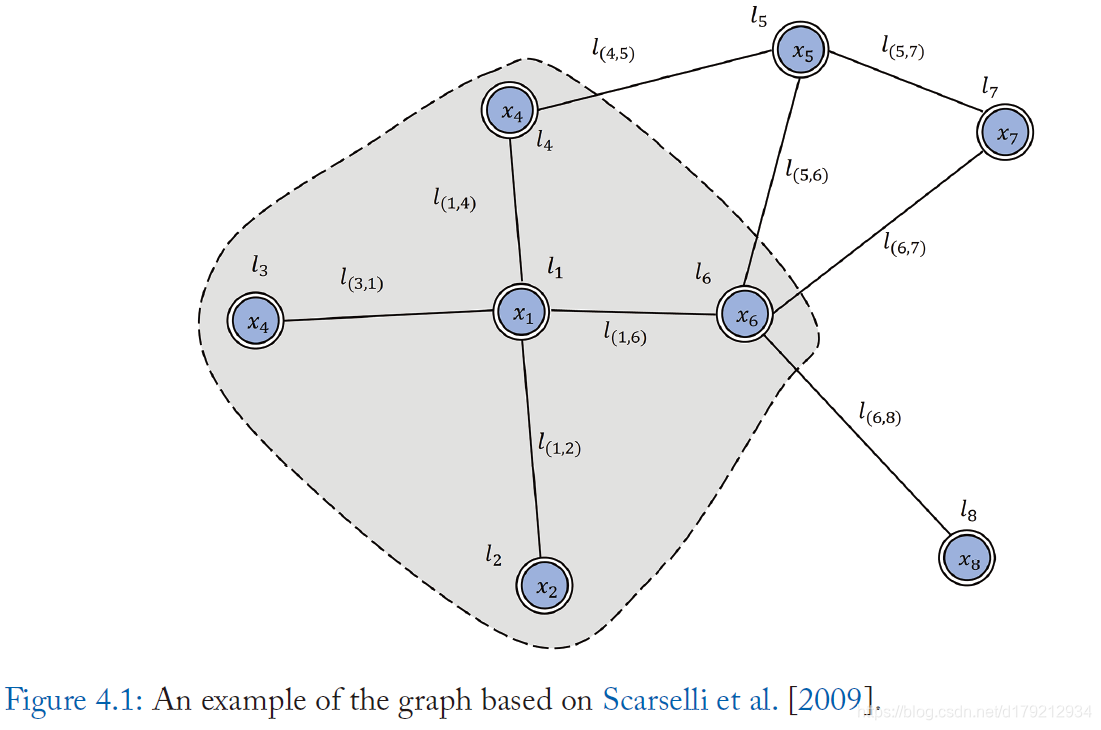
在Scarselli et al. [2009] 中，图4.1展示了一个典型的图结构，Vanilla GNN模型处理的是无向同构图，图中的每个节点都有其输入特征${\mathbf{x}}_v$，每个边同样有可能有自己的特征。文章中使用$co[v]$和$ne[v]$表示节点$v$边和领节点的集合。对于处理更加复杂的图如异构图，可以在后面的章节中找到GNN相应的变体。

4.2 Model

给定了节点和边的输入特征，接下来我们就讨论模型如何获得节点embedding ${\mathbf{h}}_v$和输出embedding ${\mathbf{o}}_v$。

为了根据输入领域更新节点状态，有一个参数函数$f$，称之为局部过渡函数，其所有节点共享。为了产生节点的输出，有一个参数函数$g$，称之为局部输出函数，那么，${\mathbf{h}}_v$和${\mathbf{o}}_v$的定义如下：
h v = f ( x v , x c o [ v ] , h n e [ v ] , x n e [ v ] ) (4.1) \mathbf{h}_v=f(\mathbf{x}_v,\mathbf{x}_{co[v]},\mathbf{h}_{ne[v]},\mathbf{x}_{ne[v]}) \tag{4.1} h<