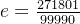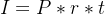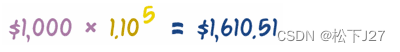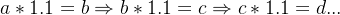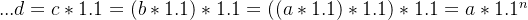自然指数函数e^x与欧拉数e (下)

自然指数函数e^x与欧拉数e

Part I: 从幂级数到欧拉数e

上一篇文章停在了“应该存在一个b，使得指数函数b^x在x=0处的导数为1。且该指数函数在任意一处的导数都等于当前位置的函数值”。根据前面所知道的，可以用数学公式列出以下一些已知条件：

$f(x)=b^{x}$ （式1：表示原函数）

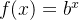
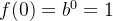
$f(0)=b^{0}=1$ （式2：表示任何指数函数的0次幂为1）

f(0)'=1 （式3：表示函数在x=0处的导数为1）

f(x)'=f(x) （式4：表示函数在任意处的导数等于y）

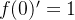
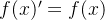
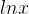
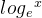
这样看来我们只需根据(式4)求解微分方程即可，但这样一来就会直接引出 lnx ，即，以e为底的对数函数 $log{_{e}}^{x}$ 。但实际上这个时候我并不知道e，这让我很苦恼。因为，我所看到的数学书里面基本上都是先讲对数，再讲 lnx ，然后再讲对数函数的反函数，一直到引出e^x和e。所以，我在这里试图改用另一种方法来给出e。

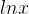
已知我要求的目标函数是f(x)=b^x，现在要基于上面的所有已知条件去构建该函数，使得b的是我们要找的那个数，他能够满足上面四个等式。

第一步：

根据(式2)，

f(0)=1

又因为(式4)，

$f(x)'=f(x)\Rightarrow f(0)'=f(0)$

第一步最终得到，

原函数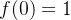
导数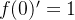

第二步：

观察第一步的结果，根据求导法则，明显，常数f(0)=1的导数f(0)'应当为0。要想让f(0)的导数f(0)'等于1，f(0)'还应该补上一个x。使得1+x的导数等于1，即：

原函数
导数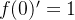

第三步：

根据(式4)导数f(0)'应该等于f(0)，因此，我们要对第二步的结果进行再一次改写，如下：

原函数
导数

第四步：

再次根据函数的求导法则，要想让导数f(0)'等于1+x，f(0)不应是1+x，而是1+x+(x^2)/2。

原函数	$f(0)=1+x+x^{2}/2$
导数

第五步：

再次根据(式4)导数f(0)'应该等于f(0)，重写导数。

原函数	$f(0)=1+x+x^{2}/2$
导数	$f(0)'=1+x+x^{2}/2$

依此类推，反复的修改原函数与导数，最终我们会得到如下的结果：

原函数	$f(0)=1+x+x^{2}/2+x^{3}/(2*3)$
导数	$f(0)'=1+x+x^{2}/2+x^{3}/(2*3)$

原函数	$f(0)=1+x+x^{2}/2+x^{3}/(23)+x^{4}/(23*4)$
导数	$f(0)'=1+x+x^{2}/2+x^{3}/(23)+x^{4}/(23*4)$

原函数	$f(0)=1+x+x^{2}/2+x^{3}/(23)+...x^{n}/(23*...n)+...$
导数	$f(0)'=1+x+x^{2}/2+x^{3}/(23)+...x^{n}/(23*...n)+...$

用阶乘符号可简化成：

原函数	$f(0)=1+x+x^{2}/2+x^{3}/(2*3)+...x^{n}/n!+...$
导数	$f(0)'=1+x+x^{2}/2+x^{3}/(2*3)+...x^{n}/n!+...$

最终我们完成了目标函数f(x)=b^x的构造，得到：

$b^{x}=1+x+x^{2}/2+x^{3}/(2*3)+...x^{n}/n!+...$

当x=0时，b^x=1，这和上面的公式吻合：

$b^{0}=1+0+0+0+...0+...=1$

但当x=1时，我们就能求出b：

$b^{1}=b=1+1+1^{2}/2+1^{3}/(2*3)+...1^{n}/n!+...$

=1+1+1/2+1/(2*3)+1/(2*3*4)+1/(2*3*4*5)+...1/n!+...

	前n项	第n项	前n项和
1	1	1	1
2	1+1	1	2
3	1+1+1/2	0.5	2.5
4	1+1+1/2+1/6	0.1666667	2.666667
5	1+1+1/2+1/6+1/24	0.0416667	2.70833333
6	1+1+1/2+1/6+1/24+1/120	0.0083333	2.716666667
7	1+1+1/2+1/6+1/24+1/120+1/720	0.0013888	2.718055556
8	1+1+1/2+1/6+1/24+1/120+1/720+1/5040	0.0001984127	2.718253968
9	1+1+1/2+1/6+1/24+1/120+1/720+1/5040+1/40320	0.0000248015873	2.718278769
	。。。	。。。	。。。
n	1+1+1/2+1/6+1/24+1/120+1/720+1/5040+1/40320+...	0.0000000000001	2.718281828

最终能够求得这个非常特别的b的近似值，他是一个无限不循环小数。以瑞士数学家欧拉(Euler)命名，被称为欧拉数，并取其名字的首字母e来特指这一数。至此，我们就得到了自然指数函数，他不在被写作b^x，而是用e^x来特指这一函数，叫做自然指数函数(在有些地方会直接称之为指数函数)：

$f(x)=b^{x}\Rightarrow f(x)=e^{x}$

至此，我们得到了自然指数函数的幂级数(power series)表示形式：

$e^{x}=\sum_{n=0}^{\infty }\frac{x^{n}}{n!}=1+x/1!+x^{2}/2!+x^{3}/3!+...$

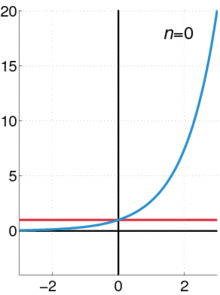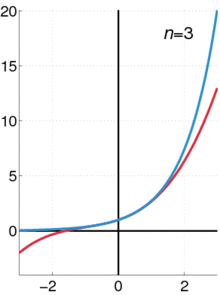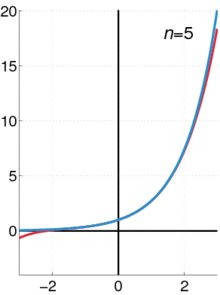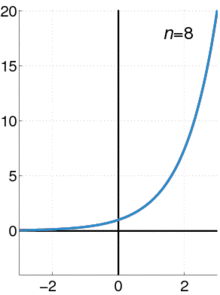
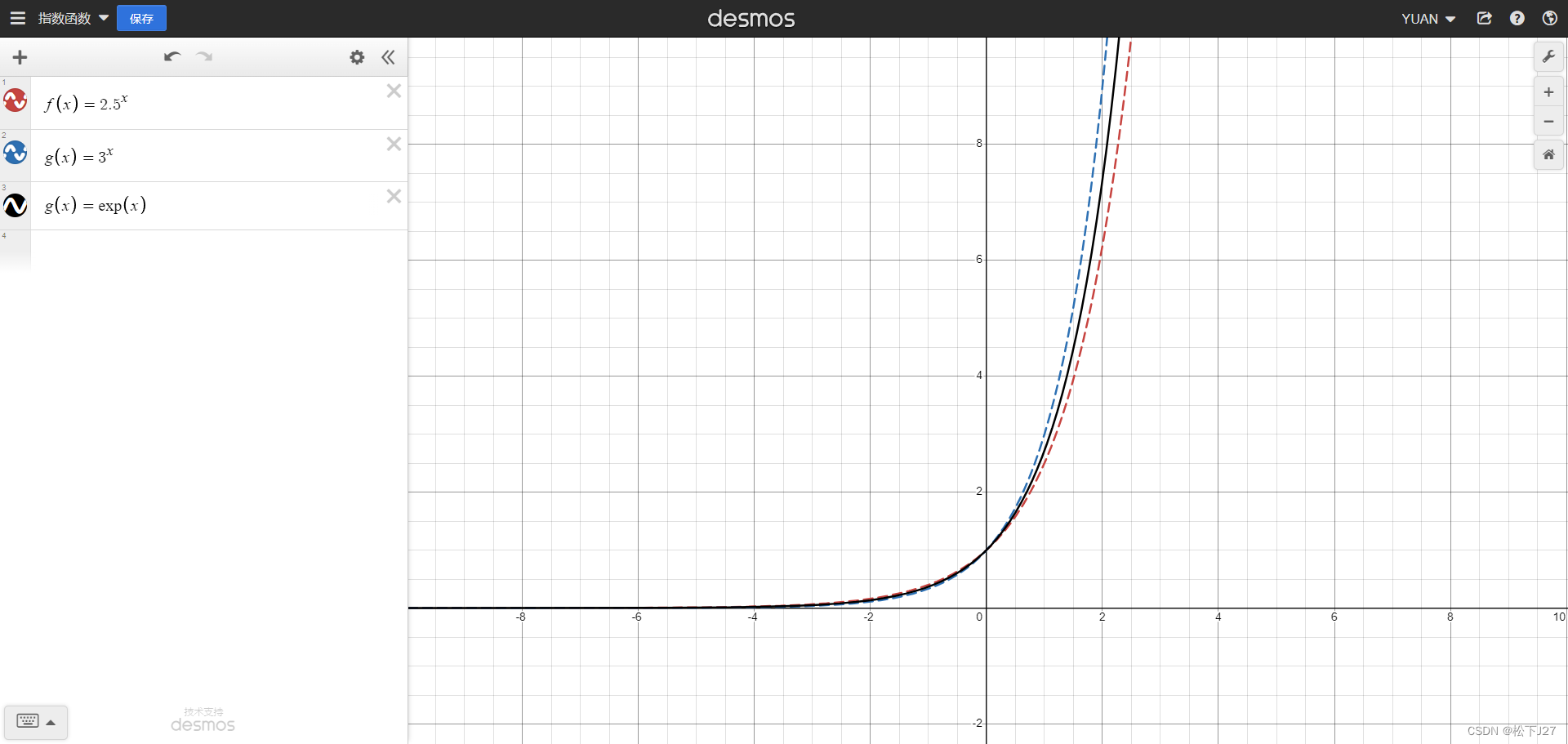
下图展示了随着项数n的增加，自然指数函数的变化过程，图中蓝线为自然指数函数的曲线。

e的近似值可以用一个有理数来表示：

$e=\frac{271801}{99990}$

下图为b=e=2.71828...时自然指数函数的图像，他正好位于b=2.5和b=3之间。

此外，自然指数函数的导数图像和原函数的图像是一样的：

Part II: 复利(compound interest)---欧拉数e的另一种计算方式

先从利息（Interest）谈起！

单利，simple interest

假设我(松下J27)想从银行借1000块钱，借的这1000块钱叫本金(Principal)。银行说，借钱可以，但我不能白借给你。等你还钱的时候，你不光要还1000块钱的本金，你还要付一点利息。如果一年的利息/利率(interest)是10%。那就是说，我借了这1000块钱，一年以后我要偿还的利息是：

连本带利我总共要还给银行的是1100元。其中1000叫本金(Principal),100是利息(interest)。

如果是借5年呢：

连本带利总共要还1500元。

上面说的这种计算利息的方式叫做单利(simple interest)，这是一种按照固定本金的计算方式。

单利的计算方式为(连本带利)：

T=P+P*r*t=P*(1+r*t)

其中：

T=total，表示连本带利总共需要还款的金额

P=Pincipal，表示本金

r=Interest rate，表示利息/利率(就上面的那个例子而言表示"年利率"）

t=Time，表示总的借款时间(就上面的那个例子而言表示"年")

单利的计算方式为(只计算利息)：

I=P*r*t

其中：

I=Interest，表示连本带利总共需要还款的金额

P=Pincipal，表示本金

r=Interest rate，表示利息/利率(就上面的那个例子而言表示"年利率"）

t=Time，表示总的借款时间(就上面的那个例子而言表示"年")

复利，compound interest(年利率)

要是事情就这么简单的继续下去就好了。遗憾的是，银行往往都不会用这种方式来计算利息，而是用复利(Compound Interest)。所谓复利，就是旧社会高利贷的一种计算方式，是人们口里常说的“驴打滚，利滚利”，是一种剥削人民的手段。

还是接着上面的那个例子说，如果我想从银行借1000块钱，第一年的利息依然是100，但改成用复利的计算方式后，从第二年开始利息就变了。第二次计算利息时，需要把前面的利息并入本金一同计算利息，得到110。依此类推，如下图所示：

注意：每次计算时本金的改变

这样算下来，同样贷款5年连本带利总共要还1610.51元。比用单利的计算利息整整多出来了1610.51-1500=110.51元。

单从计算的角度看，10%的利息相当于是用本金乘以1.1就能得到计算结果。因此，为了计算方便，我们可以把上述计算过程改写成如下方式：

更进一步，如果我们把上面的式子用代数来表示可得：

$a*1.1=b\Rightarrow b*1.1=c\Rightarrow c*1.1=d...$

现在我们对上式改写，得到：

$...d=c*1.1=(b*1.1)*1.1=((a*1.1)*1.1)*1.1=a*1.1^{n}$

本例是5年，代入金额后得到：

复利的计算方式为(连本带利)：

$T=P*(1+r)^{t}$

其中：

T=total，表示连本带利总共需要还款的金额

P=Pincipal，表示本金

r=Interest rate，表示利息/利率(就上面的那个例子而言表示"年利率"）

t=Time，表示总的借款时间(就上面的那个例子而言表示"年")

复利的计算方式为(只计算利息)：

$T=P*((1+r)^{t}-1)$

其中：

T=total，表示连本带利总共需要还款的金额

P=Pincipal，表示本金

r=Interest rate，表示利息/利率(就上面的那个例子而言表示"年利率"）

t=Time，表示总的借款时间(就上面的那个例子而言表示"年")

一年内分多期计算复利

注意，到目前为止计算复利都是按年利率计算，也就是给你年利率并按照年来计息。但如果把年利率掰成多次来算呢，换句话说就是在一年内按照多次来计息，还款利息又会发生什么变化？

例如：

把10%的年利率按照两个半年来计算复利，也就是一年内计息两次，每次计息时的本金都要加上上一次的利息。

首先，如果是每半年计算一次复利，需要把年利率除2得到半年的利息。

上半年的利息是：5%

下半年的利息是：5%

按照5%的利率算，一年后连本带利要还1102.5，比原来的计息方式多了1102.5-1100=2.5。

奇怪，明明是10%的年利率，一年分两期来计算后，利息居然变成了10.25%！这个新的年利率 $r_{valid}$ 被称之为有效年利率(Effective Annual Rate)。

如何计算和使用有效年利率( $r_{valid}$ )呢？我们只需把上面的计算过程用数学公式重写一遍就能理清思路了。

首先，年利率r分两期计算复利，得到分期利息：

0.1/2=0.05

齐次，先算上半年的利息，得到：

1000*0.05

加上本金后：

1000+1000*0.05

再算下半年利息：

(1000+1000*0.05)*0.05

再加上之前的本金，得到最终连本带利要还的钱：

1000+1000*0.05+(1000+1000*0.05)*0.05

合并同类项：

1000+1000*0.05+(1000+1000*0.05)*0.05

=(1000+1000*0.05)*(1+0.05)

=1000*(1+0.05)*(1+0.05)

=1000*(1+0.05)^2

=1000*(1+0.1/2)^2

其中“0.1”是原始的年利率10%，“2”是一年内分期的次数，共分2期。如果把上面的计算过程用代数来表示的话，我们就能推导出一年内分多期计算复利的公式。

一年内分期计算复利的计算方式为(连本带利)：

$T=P*(1+r/n)^{n}$

（注意:这个公式只适用于计算一年的利息）

其中：

T=total，表示连本带利总共需要还款的金额

P=Pincipal，表示本金

r=Interest rate，表示年利率

n，表示一年内总共分几期计算复利

此外，在上面的计算结果的基础上减去原始本金1000：

1000*(1+0.1/2)^2-1000

合并同类项：

1000*(1+0.1/2)^2-1000

=1000*((1+0.1/2)^2-1)

其中“0.1”是原始的年利率10%，“2”是一年内分期的次数，共分2期，“1000”是本金。把式子的后部分单独拎出来，这就是新的年利率：

((1+0.1/2)^2-1)=0.1025，即10.25%

同样，把上面的计算过程用代数来表示，就得到了有效年利率的计算公式。

有效年利率的计算方式为：

$r_{valid}=(1+r/n)^{n}-1$

其中：

$r_{valid}$ =Effective Annual Interest rate，表示有效年利率，也就是经过计算后得到的新的年利率

r=Interest rate they mentioned，表示原始年利率，也就是最开始提出的年利率

n，表示一年内分多少期计算复利

知道了怎么计算有效年利率(也就是实际年利率)后，我们就可以直接用有效年利率去计算存款n年后的利息了。

基于有效年利率计算复利的方式为(连本带利)：

$T=P*(1+r_{valid})^{t}$

其中：

$r_{valid}$ =Effective Annual Interest rate，表示有效年利率，也就是经过计算后得到的新的年利率

T=total，表示连本带利总共需要还款的金额

P=Pincipal，表示本金

r=Interest rate，表示年利率

n，表示一年内总共分几期计算复利

现在拿前面的例子做个实验，按照半年计算复利，年利率10%，共存5年。

首先计算有效年利率：

$r_{valid}=(1+r/n)^{n}-1=(1+0.1/2)^{2}-1=0.1025$

接下来用新公式计算本息：

$T=P*(1+r_{valid})^{t}=1000*(1+0.1025)^{5}=1628.89$

注意：如果按年来计算复利的结果是1610.51。

一年之内分期的次数越来越多会怎么样？

现在我们知道了如何利用有效年利率计算n年之后的复利，让我们回过头来看看一年以内按不同方式来分期计算复利的情况。前面我们只讨论了一年内分上半年和下半年分两期来计算复利的方式。现在我们可以试着分更多期计算复利，并观察利息的变化。

如果每年分四个季度来计算复利，n=4，有效年利率为：

$r_{valid}=(1+r/n)^{n}-1=(1+0.1/4)^{4}-1=0.1038$

t=5，连本带利总共要还：

$T=P*(1+r_{valid})^{t}=1000*(1+0.1038)^{5}=1638.62$

如果按月来计算复利，n=12，则有：

$r_{valid}=(1+r/n)^{n}-1=(1+0.1/12)^{12}-1=0.1047$

$T=P*(1+r_{valid})^{t}=1000*(1+0.1047)^{5}=1645.31$

如果是按天算呢，n=365：

$r_{valid}=(1+r/n)^{n}-1=(1+0.1/365)^{365}-1=0.1052$

$T=P*(1+r_{valid})^{t}=1000*(1+0.1052)^{5}=1648.61$

可见，随着分期计息方式的方式的改变，准确的说是随着把按年计算复利的方式改成一年内分越来越多次计算复利后，我们总共要还的钱变得越来越多！如果把年利率再继续分下去呢？比如说按半天，按小时，按分钟，等等。我们要还的钱会一直涨下去吗？

不会，他会趋近于一个常数，或者说是无限的趋近于一个极限，且这个极限和e息息相关。

我们把计算有效年利率的计算公式做一些调整:

令

x=n/r

则

$r/n\Rightarrow 1/x$

$n\Rightarrow x*r$

使得

$r_{valid}=(1+r/n)^{n}-1=(1+1/x)^{x*r}-1=((1+1/x)^{x})^{r}-1$

Tips:

$(x^{a})b=x^{a*b}$

现在把焦点放到调整后的公式的这一部分：

因为，x=n/r中r是固定的，但n一直在涨(n是分期的次数)，当n趋近于分无穷多份计算利息的话。x就会趋向于无穷大。这时，上图红色部分的就会无限的趋近于一个定值：

	$(1+1/x)^{x}$
1	2
2	2.25
5	2.48832
10	2.59374
100	2.70481
1000	2.71692
10000	2.71815
100000	2.71827
...	...

这个趋近于稳定的一个数，是一个无限不循环的数，也就是欧拉数e。

$\mathbf{e=2.71828...}$

至此，我们终于通过一年内分多期去计算复利的思路求出了欧拉数e。同时，也得出了计算连续复利的公式。即，当n趋近于无穷大时，有效年利率得公式变成：

$r_{valid}=((1+1/x)^{x})^{r}-1=e^{r}-1$

基于连续复利，求有效年利率的方式为：

$r_{contious\: valid}=e^{r}-1$

其中：

e，表示欧拉数

$r_{contious\: valid}$ ，表示按照一年内分无穷多期计算复利的方式所求得的有效年利率，这里暂且称之为连续复利有效年利率

基于连续复利算出的有效年利率，计算复利的方式为(连本带利)：

$T=P*(1+r_{contious\: valid})^{t}$

其中：

T=total，表示连本带利总共需要还款的金额

P=Pincipal，表示本金

$r_{contious\: valid}$ ，表示按照一年内分无穷多期计算复利的方式所求得的有效年利率，这里暂且称之为连续复利有效年利率

t，以年为单位，表示总共要存多少年

例如：本金1000块，年利率为10%，按照连续复利计算共存5年。

先求连续复利有效年利率：

$r_{contious\: valid}=e^{0.1}-1\approx 0.105171$

$T=P*(1+r_{contious\: valid})^{t}=1000*(1+0.105171)^{5}=1648.722$

这比之前n=365(即按365天分期计算复利)算出来的1648.61又多出来了0.112元。

（全文完）

作者 --- 松下J27

格言摘抄：

命运是对手，永不低头！

参考文献(鸣谢)：

1，指数

2，指数、根和对数

3，指数函数参考

4，https://en.wikipedia.org/wiki/Exponentiation

5，Thomas' calculus(12th edition), page 41

6，calculus-James Stewart(2015), page 413

7，[oCourse][中英][微积分重点][MIT][Strang]4_指数函数_哔哩哔哩_bilibili

8，e――欧拉数

9，复利――定期复利

10，Compound Interest - Periodic Compounding

（配图与本文无关）