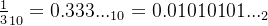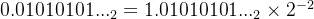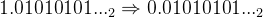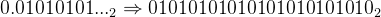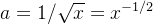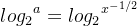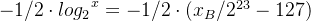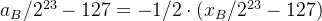平方根倒数快速算法(中) --- 向Greg Walsh致敬!
在前面的介绍中,我们已经知道了这段代码的作者Greg Walsh在函数的最后使用了NR-iteration,且只用了一次NR-iteration就能达到比较理想的精度。这样一来,选择正确的初值就显得尤为重要了。而选择初始值的关键又在于充分的利用浮点数x在计算机中的表示/编码方式。
1,计算机浮点数的二进制表示IEEE-754
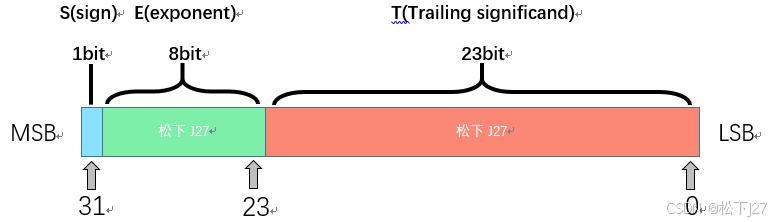
在code中函数的输入number为一个float型的浮点数(注意:代码中的number就是我文中的x)。则根据标准IEEE 754,x的二进制浮点数表示如下(准确的说应该叫normal number的表示标准),其中,S表示符号位,E表示指数,T表示有效数字的尾数:
对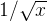
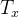
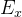
在IEEE-754标准中,对于单精度float而言,精度p=24,指数部分的偏移量b=127,则:
,(式1)
2,二进制浮点数x的对数表达式 --- log2(x)
我们对x的二进制浮点数表示(式1)取以2为底的对数,得到:
,(式2)
使用整体替换,令:
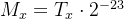
把(式3)中的整体替换代入(式2),则(式2)变为:
得到:
,(式4)
3,log2(1+M)的近似
根据IEEE-754的标准,T字段所保存的是trailing significand,即,放大一定精度后的有效数字的尾数或者说是放大一定精度后的有效数字的小数部分(不保存整数部位的1)。计算机在保存T时,是先把小数点右移了23位,即,乘以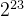

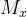
为了更好的理解M,这里插播一个例子。比如说,数1/3是如何被保存成二进制浮点数的?
计算机使用二进制浮点数表示小数时,采用的是IEEE 754浮点数标准。1/3是一个无限循环小数,计算机在保存他的时候不能都存下来,所以计算机只能保存到一定精度。
1. 十进制转二进制
在十进制下,1/3=0.33333...是一个循环小数。转换到二进制后为:
也是一个二进制的循环小数,但由于计算机只能只能保存有限的位数,这个循环小数在保存时会被截断,得到一个近似值。
2. IEEE 754 浮点数表示
在 IEEE 754 单精度浮点数标准中,32位浮点数的表示结构如下:
- 1 位符号位:表示正数或负数
- 8 位指数:存储实际指数的偏移量(偏移 127)
- 23 位尾数(有效数字):存储归一化的尾数,隐含首位为 1 的小数部分
对于1/3,计算机会先将其转换为二进制表示,然后使用以下步骤:
1,标准化二进制小数:将二进制小数表示成规范形式。规范形式要求小数点左侧只能有一位,且必须是1,因此:
2,计算指数E:指数部分需要加上偏移量(127)。所以,计算机所保存的指数E等于上面的实际指数−2加上127。−2+127=125,再转换为二进制后为 01111101。
3,有效数字的尾数T:有效数字尾数的精度共 23 位,因此我们在保存小数部分时,去掉整数部分的1不保存:
然后再把小数点右移23位,得到:
4,最终的存储形式:将符号位(0,正数)、指数(125 的二进制表示01111101)和有效数字的尾数组合起来,得到:
这就是1/3在IEEE 754标准下的单精度二进制浮点数表示。
由于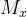
Matlab code:
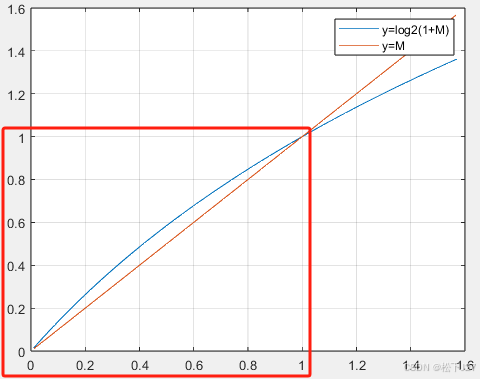
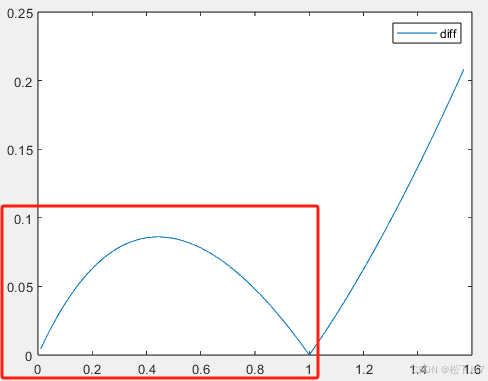
close all clear all M=0.01:0.01:pi/2; f1=log2(1+M); f2=M; plot(M,f1,M,f2); grid on; legend("y=log2(1+M)","y=M") diff=abs(f1-f2); figure plot(M,diff) legend("diff")
基于上面二者的微弱差异,我们暂且认为在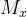
,(式5)
基于(式5)的近似,(式4)变为:
,(式6)
若再把之前的整体替换(式3)代回到(式6)中,则:
得到:
,(式7)
又因为(式7)括号中的,正好是浮点数x在计算机中的存储形式(我们这里用
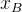

这里,我们再补充说明一下。如果还是以上面插播的1/3为例的话。我文章中的x就是十进制的1/3,而
就是上面那个例子中最终保存的
。他们是同一个数,只不过一个是平常看到的十进制数,一个是这个十进制数在计算机中保存的样子。
4,二进制浮点数x对数表达式的通式
如此一来,我们利用浮点数x在计算机中默认的二进制存储方式(也就是(式8)),再度改写了浮点数x的对数表达式(式7)(最初的对数表达式为(式4)):
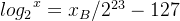
5,神秘数字 --- “5f3759df”
现在我们再回到计算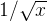
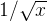
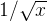
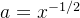
对(式10)两边同时取以2为底的对数,得到:
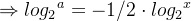
根据前面推导出的log2(x)的表示方式(式9),则(式11)的左右两边分别变为:(注意前面推导出(式9)的是一个通式,即可以表示log2(x),也可以表示log2(a),log2(b),log2(c)。。。等)
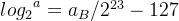
最终(式11)变为:
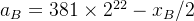
此处的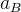
(式12)中的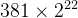
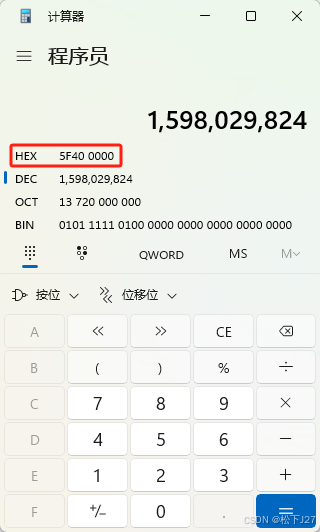
则(式12)可改写为:

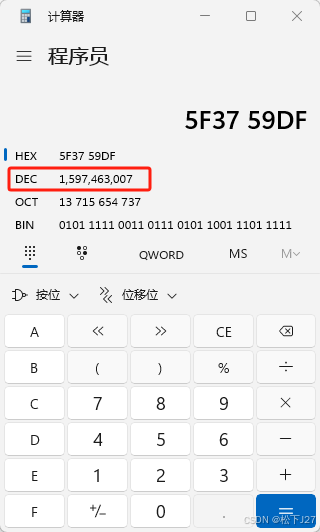
这里的十六进制数“5f400000”和code中的那个神秘数字“5f3759df”已经比较接近了,而5f3759df表示成十进制是1597463007。
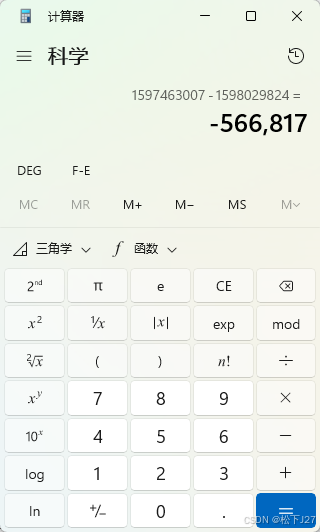
两者在十进制上相差了566817。
6,锐评"what the fuck?"的上下两句在干啥?
这里,我们暂时先不讨论这两个十六进制常数的差异,先看看(式13)究竟表示什么意思:

首先,我们知道a就是我们要求的十进制数x的平方根倒数,而我们又知道不论十进制数a或x是多少,他在计算机中都要以二进制浮点数的方式被保存为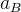
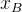
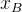
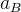
而要想求得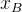
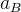
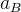
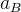
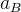
现在让我们再回到原代码,请注意,被评论为WTF的上下两句所做的,正是我上文中描述的过程。所不同的是代码中的y是我文中的x,代码中的i是我文中的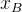
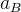
现在,我们有了能够快速求出较为精确的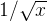
。至此,我们基本上复现了平方根倒数快速算法的全部过程,且和原始code一致(除了magic number之外)。
7,小试牛刀
我们来试试我们现有的快速算法,看看他的效果究竟怎么样,还是以x=1为例,求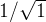
C code:
# include <stdio.h> # include <math.h> float Q_rsqrt(float number) { long i; float x2, y; const float threehalfs = 1.5F; x2 = number * 0.5F; y = number; i = *(long*)&y; // evil floating point bit level hacking i = 0x5f3759df - (i >> 1); // what the fuck? y = *(float*)&i; y = y * (threehalfs - (x2 * y * y)); // 1st iteration // y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed return y; } float myQ_rsqrt(float number) { long i; float x2, y; const float threehalfs = 1.5F; x2 = number * 0.5F; y = number; i = *(long*)&y; // evil floating point bit level hacking i = 0x5f400000 - (i >> 1); y = *(float*)&i; y = y * (threehalfs - (x2 * y * y)); // 1st iteration // y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed return y; } int main() { float x = 4.0f; float y = 0,yy=0; y=Q_rsqrt(x); yy = myQ_rsqrt(x); printf("input x=%f\n", x); printf("ideal result=%f\n", 1/sqrt(x)); printf("calc with 5f3759df=%f\n", y); printf("calc with 5f400000=%f\n", yy); return 0; }
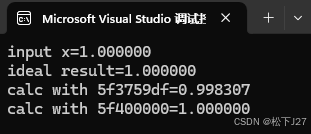
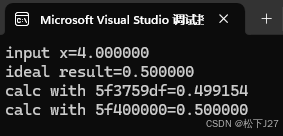
code相应的输出为:
就本例而言,二者的计算结果都非常接近准确值1。5f400000的精度更高,几乎没有精度误差,5f3759df的误差约为0.002。
如果以x=4为例,参考准确值为0.5,再看看二者的表现:
结果还是5f400000的准确性更高,同样是几乎等于标准答案。但5f3759df的误差约为0.0009。上面的两个例子都是平方根的结果正好是整数的情况,例如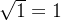
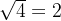
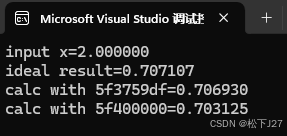
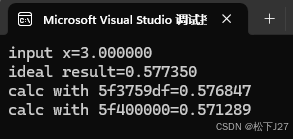
如果碰到平方根为无理数的情况呢?我们分别试试x=2和x=3的情况。
有趣的是,在这两个例子中基于5f3759df的计算结果要比5f400000的精度高。其中,对于x=2而言,5f400000的误差约为0.004 > 5f3759df的误差约为0.0002。 对于x=3而言,5f400000的误差约为0.006 > 5f3759df的误差约为0.0005。
这样看来,不论是采取哪种常数去估算初值,基本上都已经能够得到较为准确的结果。如果还需要得到更精确的结果,可用牛顿拉夫逊法再迭代一次即可。关于平方根倒数快速算法code的分析至此就全部写完了,后续我会再写一些关于神秘数---5f3759df的思考。
(全文完)
--- 作者,松下J27
参考文献(鸣谢):
1,https://en.wikipedia.org/wiki/Newton%27s_method#Examples
2,什么代码让程序员之神感叹“卧槽”?改变游戏行业的平方根倒数算法_哔哩哔哩_bilibili
3,[算法] 平方根倒数速算法中的魔数0x5f3759df的来源 | GeT Left
4,https://i.hsfzxjy.site/uncover-the-secret-of-fast-inverse-square-root-algorithm/
5,https://www.youtube.com/watch?v=p8u_k2LIZyo
8,Beyond3D - Origin of Quake3's Fast InvSqrt()
9,Beyond3D - Origin of Quake3's Fast InvSqrt() - Part Two
10,The Fast Inverse Square Root
11,How Fast Inverse Square Root actually works
版权声明:所有的笔记,可能来自很多不同的网站和说明,在此没法一一列出,如有侵权,请告知,立即删除。欢迎大家转载,但是,如果有人引用或者COPY我的文章,必须在你的文章中注明你所使用的图片或者文字来自于我的文章,否则,侵权必究。 ----松下J27