一、前言
数据结构在逻辑结构上分为线性和非线性,例如链表、顺序表、串、数组都是线性的,他们的特点就是一对一,而非线性结构比如图和二叉树,他们的对应关系是一对多、多对多,这里介绍线性表的顺序表和链表、循环链表和双向链表,还有双向循环链表。链表尤其重要,很多结构都是以链表作为基础的,比如栈和队列。
两个基本特征:
1.线性表中所有元素所占的存储结构空间是连续的
2.线性表中各数据元素在存储空间中按逻辑顺序存放
二、顺序表——顺序存储结构
顺序表的特点概念
顺序表所开辟的内存是固定的,不能自动调整所分配的内存大小,在内存上是连续分布的,存在一对一的关系。

2.在类中的功能实现
1.结点定义
2.初始化顺序表
3.查找算法
4.删除算法
5.插入算法
6.返回长度
C++代码实现
先写头文件,然后是功能实现的cpp
#ifndef TABLE_H_
#define TABLE_H_
#include<iostream>
#include<cstdlib>
using namespace std;
const int SIZE = 100;
typedef int Elemtype;
class Linear_list
{
private:
Elemtype elem[SIZE];
int length;
public:
Linear_list();
Linear_list(Elemtype value[],int n);
~Linear_list();
void ListInsert(int i,Elemtype e);
int ListDelete(int i);
Elemtype ListLocate(Elemtype e);
void PrintList();
Elemtype Getlength();
};
#endif#include"table.h"
#include<cstdlib>
Linear_list::Linear_list()
{
length = 0;
}
Linear_list::Linear_list(Elemtype value[],int n)
{
if(n > SIZE)
{
cout <<"illeagal"<<endl;
return ;
}
for(int i = 0;i < n;i++)
{
elem[i] = value[i];
}
length = n;
}
Linear_list::~Linear_list()
{
}
void Linear_list::ListInsert(int i,Elemtype e)
{
if(i < 1 || i > length + 1)
{
cout <<"More than the litertable's content"<<endl;
exit(0);
}
if(length > SIZE)
{
cout <<"wrong"<<endl;
return ;
}
for(int j = length;j >= i; j--)
{
elem[j] = elem[j-1];
}
elem[i - 1] = e;
length++;
}
int Linear_list::ListDelete(int i)
{
int x;
x = elem[i - 1];
for(int j = i;j < length;j++)
{
elem[j - 1] = elem[j];
}
length--;
return x;
}
void Linear_list::PrintList()
{
for(int i = 0;i < length;i++)
{
cout << elem[i] <<" ";
}
cout << endl;
}
Elemtype Linear_list::ListLocate(Elemtype e)
{
for(int i = 0;i < length;i++)
{
if(elem[i] == e)
{
cout <<"exit the 'e' in table,it locate "<<i + 1<<endl;
return elem[i];
}
}
}
Elemtype Linear_list::Getlength()
{
return length;
}三、链表——链式存储结构
链表的特点概念
链表是一种逻辑上连续,内存上分散的线性表数据结构,其基本单位为结点,每个结点分数据区和指针区。链表有单向链表、双向链表、循环链表。
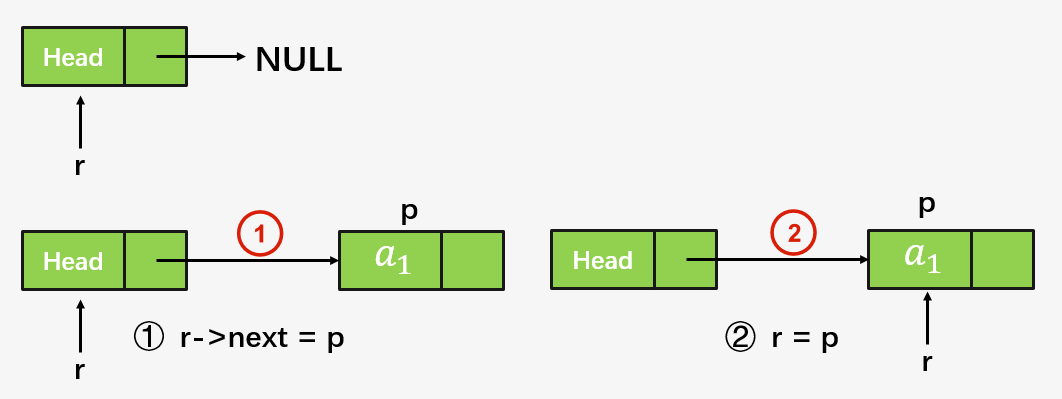
功能实现
1.结点定义
2.初始化顺序表
3.查找算法
4.删除算法
5.插入算法
6.合并算法
7.返回长度
C++代码实现
#include<iostream>
using namespace std;
typedef int Elemtype;
struct Node
{
Elemtype data;
struct Node* next;
};
typedef Node* LineLink;
//初始化
bool Init(LineLink &L)
{
L = new Node;
L->next = nullptr;
return true;
}
//尾插法创建链表
void createList(LineLink &L,int n)
{
Node* r = L;
for(int i = 0; i < n;i++)
{
Node* p = new Node;
cout <<"Please enter the data: ";
cin >> p -> data;
cout <<endl;
p->next = nullptr;
r->next = p;
r = r->next;
}
}
//头插法创建链表
void createList_r(LineLink &L,int n)
{
for(int i = 0;i < n;i++)
{
Node *p = new Node;
cout<<"Please ebter the data: ";
cin >> p->data;
cout<<endl;
p->next = L ->next;
L->next = p;
}
}
//查找算法
bool Search(LineLink &L,int i,Elemtype &e)
{
Node* p = L->next;int j = 1;
while( p && j < i)
{
p = p->next;
++j;
}
if(!p || j>i)
return false;
e = p->data;
return true;
}
//销毁算法
bool DestoryLink(LineLink &L)
{
Node* p;
while(L)
{
p = L;
L = L->next;
delete p;
}
return true;
}
//获得链表长度
int getlength(LineLink &L)
{
Node* p = L->next;
int count = 0;
while(p)
{
p = p->next;
count++;
}
return count;
}
//插入算法
bool LineInsert(LineLink &L,int i,Elemtype e)
{
Node* p = L->next; int j;
while(p && j < i -1)
{
p = p->next;
j++;
}
if(!p || j > i-1)
return false;
Node *s = new Node;
s->data = e;
s->next = p->next;
p->next = s;
return true;
}
//删除算法
bool LineDelete(LineLink &L,int i,Elemtype &e)
{
Node* p = L;;int j = 0;
while(p && j < i -1)
{
p = p->next;
j++;
}
if(!p || j > i-1)
return false;
Node *q = new Node;
q = p->next;
e = q->data;
p->next = q->next;
delete q;
return true;
}
//两个链表合并
void MergeList(LineLink &La,LineLink &Lb,LineLink &Lc)
{
Node *pa = La->next;
Node *pb = Lb->next;
Lc = La;
Node *pc = Lc;
while(pa && pb)
{
if(pa->data <= pb->data)
{
pc->next = pa;
pc = pc->next;
pa = pa->next;
}
else
{
pc->next = pb;
pb = pb->next;
pc = pc->next;
}
}
pc->next = (pa ? pa : pb);
delete Lb;
cout <<"Having Merged"<<endl;
}
//遍历链表
void PrintList(LineLink &L)
{
Node *p = L->next;
while(p)
{
cout <<p->data<<" ";
p = p->next;
}
cout <<endl;
}
int main()
{
LineLink L1;
LineLink L2;
LineLink L3;
Init(L1);
Init(L2);
Init(L3);
createList(L1,3);
createList(L2,3);
MergeList(L1,L2,L3);
PrintList(L3);
return 0;
}#模板类方式实现
#ifndef LISTNODE_H_
#define LISTNODE_H_
#include<iostream>
using namespace std;
typedef int Elemtype;
template<class T>
class ListNode
{
public:
T data;
ListNode<T>* next;
};
template<class T>
class LinkList:public ListNode<T>
{
public:
ListNode<T>* head;
public:
LinkList();
void CreateLinkList(int n);
void ListInsert(int i,T e);
void ListDelete(int i,T &e);
void MergeList(LinkList &La,LinkList &Lb);
int Getlength();
void Print();
};
template<class T>
LinkList<T>::LinkList()
{
this->head = new ListNode<T>;
if(!this->head)
std::cout<<"error"<<std::endl;
this->head->next = nullptr;
}
template<class T>
void LinkList<T>::CreateLinkList(int n)
{
ListNode<T>* r = this->head;
for(int i = 0;i < n;i++)
{
ListNode<T>* p = new ListNode<T>;
cin >> p->data;
p->next = nullptr;
r->next = p;
r = r->next;
}
}
template<class T>
int LinkList<T>::Getlength()
{
int x = 0;
ListNode<T>* p = this->head->next;
while(p)
{
x++;
p = p->next;
}
return x;
}
template<class T>
void LinkList<T>::ListInsert(int i,T e)
{
ListNode<T>* p = head->next;int j = 1;
while(p && j < i-1)
{
p = p->next;
j++;
}
ListNode<T>* r = new ListNode<T>;
r->data = e;
r->next = p->next;
p->next = r;
}
template<class T>
void LinkList<T>::ListDelete(int i,T &e)
{
ListNode<T>* p = head->next;int j = 1;
while(p && j < i-1)
{
p = p->next;
j++;
}
ListNode<T>* q = p->next;
p->next = p->next->next;
delete q;
}
template<class T>
void LinkList<T>::MergeList(LinkList &La,LinkList &Lb)
{
ListNode<T>* pa = La.head->next;
ListNode<T>* pb = Lb.head->next;
int la,lb;
la = La.Getlength();
lb = Lb.Getlength();
ListNode<T>* pc = new ListNode<T>[la+lb];
while(pa && pb)
{
if(pa->data < pb->data)
{
pc->next = pa;
pa = pa->next;
pc = pc->next;
}
else
{
pc->next = pb;
pb = pb->next;
pc = pc->next;
}
}
if(pa!= nullptr)
{
pc->next = pa;
}
if(pb!= nullptr)
{
pc->next = pb;
}
}
template<class T>
void LinkList<T>::Print()
{
ListNode<T>* p = this->head->next;
while(p)
{
cout << p->data;
p = p->next;
}
cout <<endl;
}
#endif四、循环链表
循环链表的定义
typedef structCLnode
{
ElemType data;
CLnode *next;
}*CircList;循环链表的初始化
voidInitList(CircList &L)
{
L = new CLnode;
L->next = L;
}注意!
·循环链表的基本操作和单链表基本上相同,唯一不同的是,由于循环链表的最后一个结点的next不再是空指针,而是指向头结点,因此,循环中的结束条件要发生变化==
单链表--------------循环链表
while(p)--------->while(p!=L)
while(p->next)--->while(p->next!=L)
五、双向链表
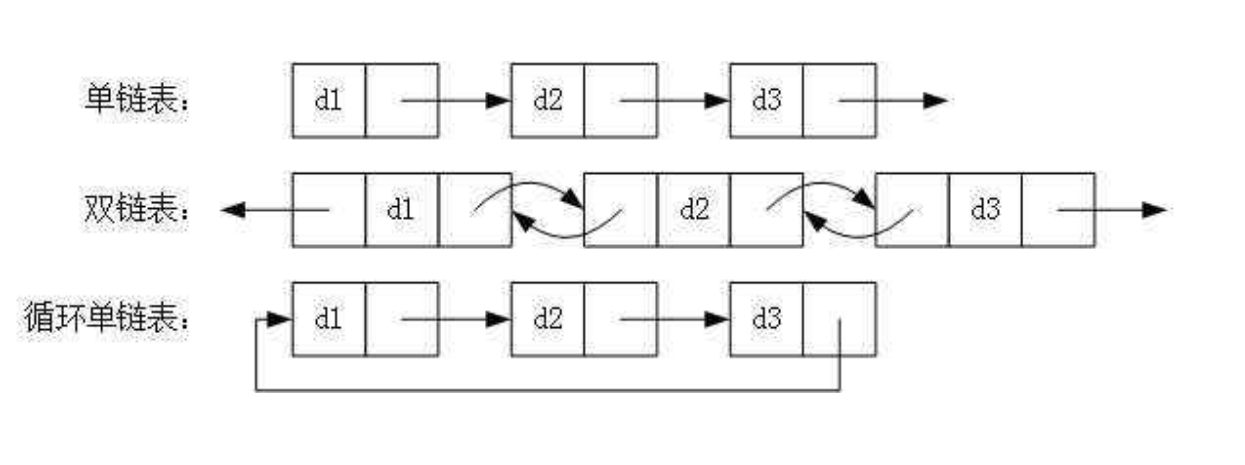
双向链表的定义
typedef int Elemtype;
struct Node
{
Elemtype data;
struct Node *prior;
struct Node *next;
};
typedef Node* LinkList;代码实现
#include<iostream>
using namespace std;
typedef int Elemtype;
struct Node
{
Elemtype data;
struct Node *prior;
struct Node *next;
};
typedef Node* LinkList;
bool Init(LinkList &L)
{
L = new Node;
L->prior = nullptr;
L->next = nullptr;
return true;
}
void CreateListTail(LinkList &L,const int n)
{
Node* r = L;
for(int i = 0;i < n;i++)
{
Node* p = new Node;
cout <<"输入内容:"<<endl;
cin >> p->data;
p->prior = r;
p->next = r->next;
r->next = p;
r = p;
}
}
int Getlength(LinkList &L)
{
Node* p = L->next;
int cnt = 0;
while(p)
{
p = p->next;
cnt++;
}
return cnt;
}
Node* GetElem(LinkList &L,int i)
{
Node *p = L->next; int j = 1;
while(p && j < i)
{
p = p->next;
++j;
}
if(!p || j > i)
cout <<"Error"<<endl ;
return p;
}
bool LinkInsert(LinkList &L,const int i,Elemtype e)
{
Node *p;
if(!(p = GetElem(L,i)))
return false;
Node *s = new Node;
s->data = e;
s->prior = p->prior;
p->prior->next = s;
s->next = p;
p->prior = s;
return true;
}
bool LinkDelete(LinkList &L,const int i,Elemtype &e)
{
Node *p;
if(!(p = GetElem(L,i)))
return false;
e = p->data;
p->prior->next = p->next;
p->next->prior = p->prior;
delete p;
return true;
}
int main(void)
{
LinkList L;
Init(L);
CreateListTail(L,3);
LinkInsert(L,1,3);
Elemtype e;
LinkDelete(L,3,e);
cout << Getlength(L) <<endl;
return 0;
}六、顺序表和链表的比较
链式存储结构的优点和缺点:
优点:结点空间可以动态申请和释放
是用指针相连,可以不移动的删除和插入元素。
缺点:
存储密度小,指针域需要额外的空间,当数据比较庞大时,可想而知。
顺序存储结构的优点和缺点:
优点:
随机存取,取数据的时候不像链表一样,从头开始查找。存储密度比较高。
缺点:
插入删除元素时,需要移动元素,时间复杂度为O(n),有可能造成溢出。

图片出自:王卓老师
七、单向链表、循环链表、双向链表的比较
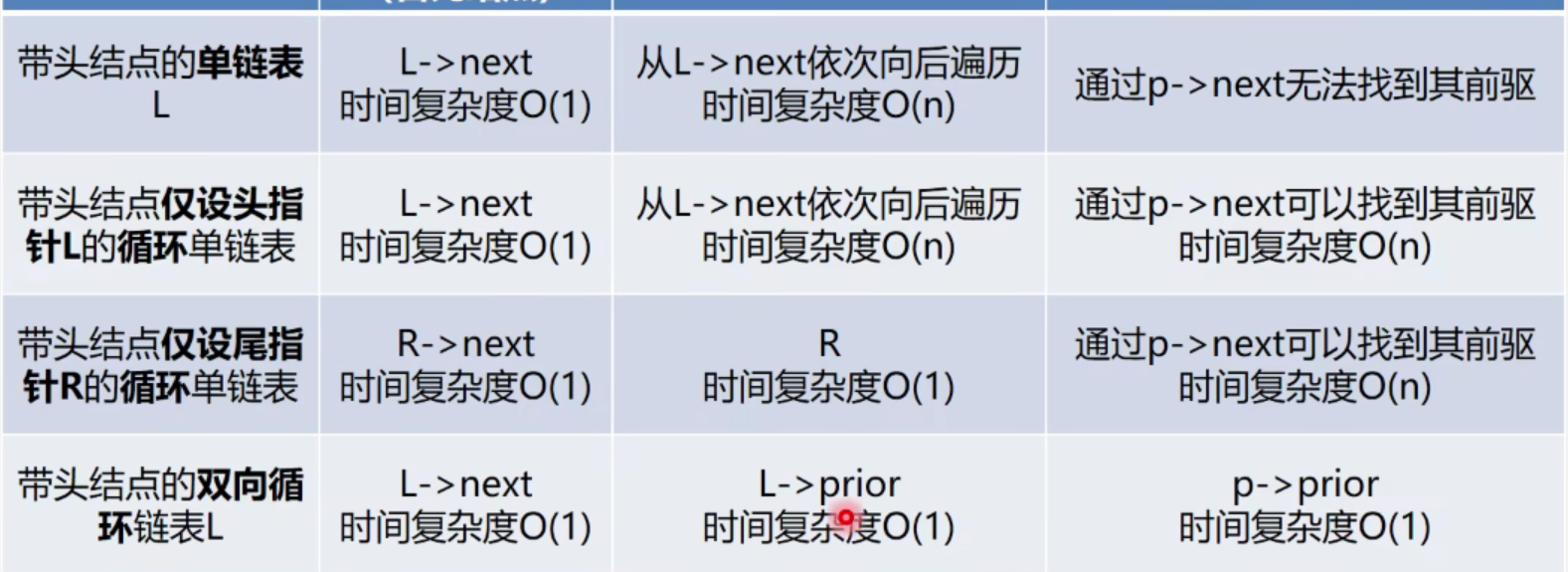
图片出自:王卓老师
八、结束语
代码是我反复测试敲过的,正确性是比较高的,如果有不足之处希望多多指教,本来全部想使用类的方法实现,但考虑到一些原因,同时也有一些问题需要改善,只有顺序表使用了类的方法,还望包涵。希望与大家继续努力。