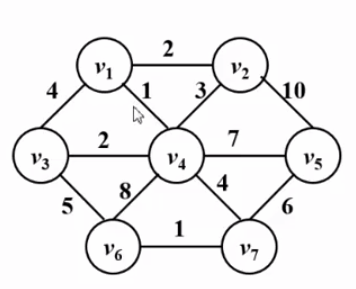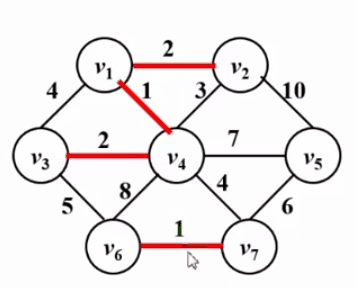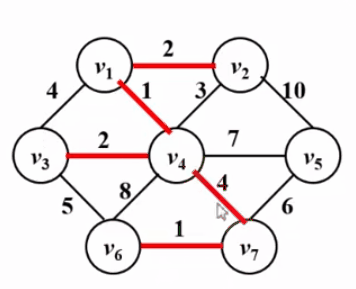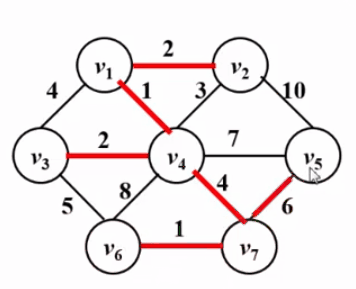
什么是图

1.定义

线性表：一对一
树：多对一
图：多对多（线性表和树是图的特殊情况）

包含：

1. 一组顶点：通常用V (Vertex) 表示顶点集合
2. 一组边：通常用E (Edge) 表示边的集合

2.抽象数据类型定义

类型名称：图（Graph）
数据对象集：$G(V,E)$由一个非空的有限顶点集合V和一个有限边集合E组成。
操作集：对于任意图$G\in Graph$，以及$v\in V$, $e\in E$
Graph Create()：建立并返回空图；
Graph InsertVertex(Graph G, Vertex v)：将v插入G；
Graph InsertEdge(Graph G, Edge e)：将e插入G；
void DFS(Graph G, Vertex v)：从顶点v出发深度优先遍历图G；
void BFS(Graph G, Vertex v)：从顶点v出发宽度优先遍历图G；
void ShortestPath(Graph G, Vertex v, int Dist[])：计算图G中顶点v到任意其他顶点的最短距离；
void MST(Graph G)：计算图G的最小生成树；

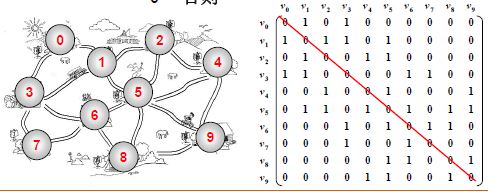
3.在程序中表示

邻接矩阵$G[N][N]$——N个顶点从0到N-1编号

$$G[i][j]=\{\begin{array}{ll}1& \text{若<vi,vj>是G中的边}\\ 0& \text{否则}\end{array}$$

对于无向图的存储，怎样可以省一半空间？

• 用一个长度为N(N+1)/2的1维数组A存储{G₀₀,G₁₀,G₁₁,……,G~n-1 0_,…,Gn-1~ _n-1}，则Gij在A中对应的下标是：$(i\ast (i+1)/2+j)$

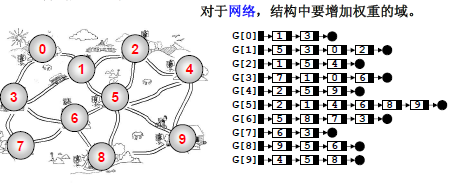
邻接表

G[N]为指针数组，对应矩阵每行一个链表，只存非0元素

图的遍历

1.深度优先搜索(Depth First Search, DFS)

类似于树的先序遍历

void DFS ( Vertex V )
{ visited[ V ] = true;
		for ( V 的每个邻接点W )
			if ( !visited[ W ] )
				DFS( W );
}

2.广度优先搜索(Breadth First Search, BFS)

void BFS ( Vertex V )
{ visited[V] = true;
	Enqueue(V, Q);   //将图V用队列存储  进
	while(!IsEmpty(Q)){
		V = Dequeue(Q);   //出
		for ( V 的每个邻接点W )
			if ( !visited[W] ) {
				visited[W] = true;
				Enqueue(W, Q);
		}
	}
}

3.连通

连通：如果从V到W存在一条**（无向）路径**，则称VW连通
路径：V到W的路径是一系列顶点{V, v₁, v₂, …,v_n, W}的集合，（任一对相邻的顶点都有图中的边）。
路径的长度是路径中的边数（如果带权，则是所有边的权重和）。
如果V到W之间的所有顶点都不同，则称简单路径
回路：起点等于终点的路径，属于复杂路径
连通图：图中任意两顶点均连通
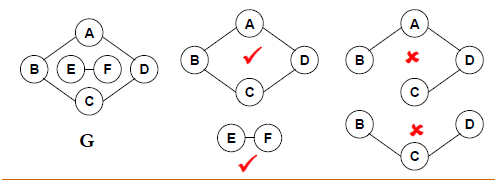
连通分量：无向图的极大连通子图

1. 极大顶点数：再加1个顶点就不连通了
2. 极大边数：包含子图中所有顶点相连的所有边

强连通： 有向图中顶点V和W之间存在双向路径，则称V和W是强连通的
强连通图： 有向图中任意两顶点均强连通
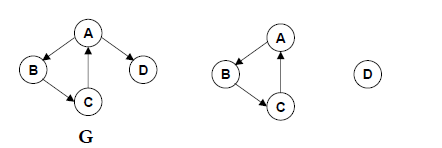
强连通分量：有向图的极大强连通子图

最短路径问题

1.定义

在网络中，两个不同顶点的所有路径中，边的权值之和最小的那一条路径，为最短路径
第一个顶点为源点（Source）
最后一个顶点为终点（Destination）

2.问题分类

单源：从某固定源点出发，求其到所有其他顶点的最短路径

• （有向）无权图
• （有向）有权图

多源：求任意两顶点间的最短路径

3.无权图的单源最短路算法

算法解析

//s到w的最短路径问题
void Unweighted ( Vertex S )
{ Enqueue(S, Q); //将源点压入
	while(!IsEmpty(Q)){
		V = Dequeue(Q); //当顶点被弹出时，表示v到源点的最短路径已被找到 
		for ( V 的每个邻接点W )
			if ( dist[W]==-1 ) {  //初始化距离为-1，表示w未被访问过
				dist[W] = dist[V]+1; //w最短距离=v的距离+1
				path[W] = V; //s 到 w 的必经顶点就是前一个顶点 v
				Enqueue(W, Q);
			  }
	}
}

4.有权图的单源最短路算法

Dijkstra 算法

算法解析

void Dijkstra( Vertex s )
{ while (1) {
	V = 未收录顶点中dist最小者;
	if ( 这样的V不存在)
		break;
	collected[V] = true;
	for ( V 的每个邻接点W )
		if ( collected[W] == false )
			if ( dist[V]+E<V,W> < dist[W] ) {
				dist[W] = dist[V] + E<V,W> ;
				path[W] = V;
				}
	}
} /* 不能解决有负边的情况*/

5.多源最短路算法

Floyd 算法

算法描述：

void Floyd()
{ for ( i = 0; i < N; i++ )
	for( j = 0; j < N; j++ ) {
		D[i][j] = G[i][j];
		path[i][j] = -1;
		}
	for( k = 0; k < N; k++ )
		for( i = 0; i < N; i++ )
			for( j = 0; j < N; j++ )
				if( D[i][k] + D[k][j] < D[i][j] ) {
					D[i][j] = D[i][k] + D[k][j];
					path[i][j] = k;
					}
}

最小生成树问题

1.定义

1. 是一棵树
   无回路
   |V|个顶点一定有|V|-1条边
2. 是生成树
   包含全部顶点
   |V|-1条边都在图里
3. 边的权重和最小
   tip：向生成树中任加一条边都一定构成回路
   最小生成树存在↔ 图连通
   

2.贪心算法

约束：

• 只能用图里有的边
• 只能正好用掉|V|-1条边
• 不能有回路

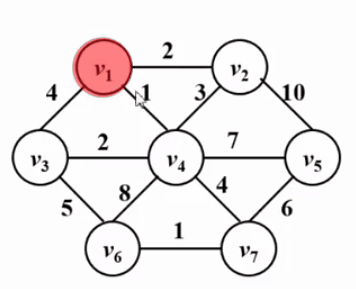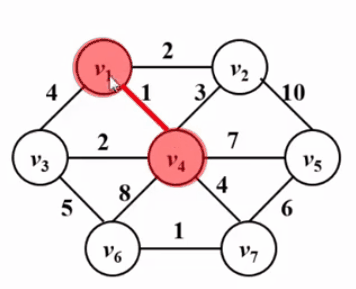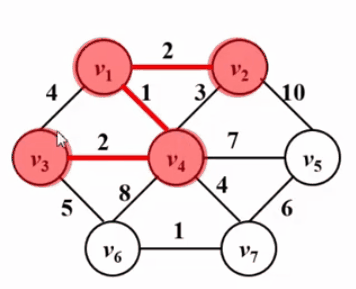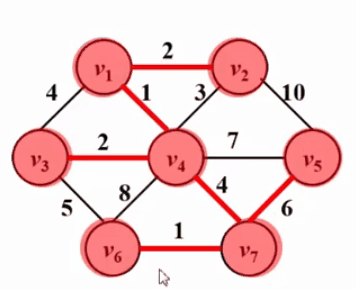
Prim算法 — 让一棵小树长大

//tip:初始化
//dist[V] = E(s,V)（已被收录）或正无穷(未被收录)；  parent[s] = -1（根结点）
void Prim()
{ MST = {s};
	while (1) {
		V = 未收录顶点中dist最小者;//dist顶点V到生成树（所有收录进去的顶点）的最小距离
		if ( 这样的V不存在)
			break;
		将V收录进MST: dist[V] = 0;
		for ( V 的每个邻接点W )
			if ( W未被收录)//即dist[W]!=0
				if ( E(V,W) < dist[W] ){
					dist[W] = E(V,W) ;
					parent[W] = V;//每个顶点储存的是父结点的编号
				}
	}
	if ( MST中收的顶点不到|V|个)
		Error ( “生成树不存在/图不连通” );
}

时间复杂度：T = O($|V{|}^2$) —— 稠密图合算

Kruskal算法— 将森林合并成树

将每个顶点都看成一棵树

void Kruskal ( Graph G )
{ MST = { } ;//收集的是边
	while ( MST 中不到|V|-1 条边&& E中还有边) {
		从E 中取一条权重最小的边E(v,w) ;//最小堆
		将E(v,w)从E 中删除;
		if ( E(V,W)不在MST中构成回路)//并查集：每个节点看成树，若两个结点在一棵树里面，则E（V,W）加入必构成回路
			将E(V,W) 加入MST;
		else
			彻底无视E(V,W);
	}
	if ( MST 中不到|V|-1 条边)
		Error ( “生成树不存在” );
}

T = O( |E| log |E| )

拓扑排序

0.背景例题：专业排课

1.定义

拓扑序：图中从V到W有一条有向路径，则V排在W之前.满足此条件的顶点序列称为一个拓扑序

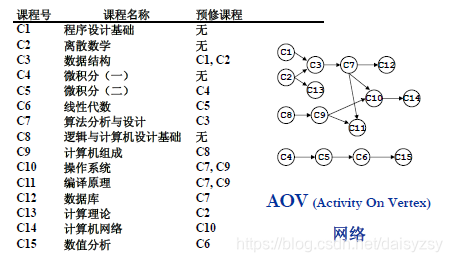
2.AOV网络

AOV（activity on vertex）：用图的顶点来代替一项工作的网络，又称顶点活动网络
如果有合理的拓扑序，则必定是有向无环图（否则v必须在v开始前结束矛盾❌）

void TopSort()
{ for ( cnt = 0; cnt < |V|; cnt++ ) {
		V = 未输出的入度为0的顶点;
		if ( 这样的V不存在) {
			Error ( “图中有回路” );
			break;
		}
		输出V，或者记录V的输出序号;
		for ( V 的每个邻接点W )
			Indegree[W]––;
		}
}

随时将入度变为0的顶点放到一个容器里

void TopSort()
{ for ( 图中每个顶点V )
	if ( Indegree[V]==0 )
		Enqueue( V, Q );
	while ( !IsEmpty(Q) ) {
		V = Dequeue( Q );
		输出V，或者记录V的输出序号; cnt++;
		for ( V 的每个邻接点W )
			if ( ––Indegree[W]==0 )
				Enqueue( W, Q );
	}
	if ( cnt != |V| )
		Error( “图中有回路” );
}

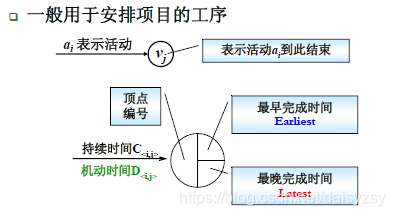
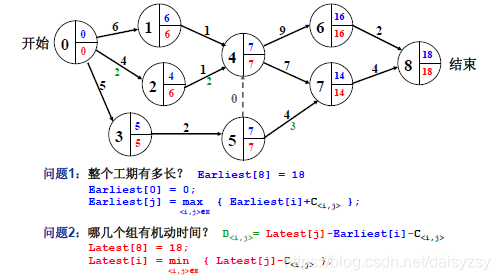
3.AOE网络

AOE（activity on edge)：用边来代替一项工作的网络

关键路径问题:由绝对不允许延误的活动组成的路径