算法力扣刷题记录五【59.螺旋矩阵II】

前言

第五篇，继续。
力扣【59】：螺旋矩阵II
（Hint: 我认为blog记录得到最终代码的过程，所以有些代码片是逻辑错误（会标明“有错”），体现改进，所以阅读时请不要错位，或复制错误代码。）

一、题目阅读和理解

题目阅读

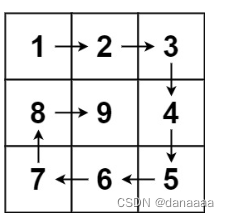
给你一个正整数 n ，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：
在这里插入图片描述

输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]

提示：

1 <= n <= 20

二、第一次尝试

思路：阅读时可以画图更明白

（1）不成功；

我首先画n <= 5的顺时针过程，第一步发现：行列交错填充数组。所以：

定义一个bool=0（初始值）;
if(bool=0)，操作行，结束时bool=1；

else，操作列。在一个for循环内。

  过程如下：
  for(int k = 0; k < xxx;k++){		//xxx代表还没确定范围，需要根据n找规律。
  	if(!bool){
  		//操作行
  	}else
  		//操作列
  }

行不通，原因，循环条件不统一：

1. 在操作行/列，for循环变量i一会向右，i++;一会向左，i--；
2. 另外for循环变量i的初始值每次也不一样，所以循环条件一直在动。

难道还要if判断什么时候++，什么时候--？那我要加的if好多，所以换思路。

（2）成功

第二步发现：

循环操作：向→；再↓；再←；再↑。4个为一组，看作一轮。所以有了大框架：

  for(int k = 0;k < (2*n-1);k++){		//为什么k < (2*n-1)，看下一点找规律
  	 switch(k % 4){
  	 	case 0:             //方向向右
  	 		//执行操作；
  	 		break;
  	 	case 1:		        //方向向下
  	 		//执行操作；
  	 		break;
  	 	case 2:             //方向向左
  	 		//执行操作；
  	 		break;
  	 	case 3:             //方向向下
  	 		//执行操作；
  	 		break;
  	 }
  	 //xxxx  后面分析还要加什么。
  }

n=2时，3步：向→；再↓；再←；
n=3时，5步：向→；再↓；再←；再↑；向→；
n=4时，7步：向→；再↓；再←；再↑；向→；再↓；再←；
n=5时，9步：向→；再↓；再←；再↑；向→；再↓；再←；再↑；再→；

所以for循环的范围是k < (2*n-1)。

接着填充每个方向内的代码，即case下的代码，完成矩阵元素填充：

以向右操作case0，作完整分析：（其余类似）

首先想到for循环：

  	int i=0；//行坐标
  	int j = 0;//列坐标
  	case 0：
  		for(;j <= line; j++) {//初始值——没有固定值，先不写；范围——line每次减1，初始值(n-1)；向右，所以j++
  			matrix[i][j] = num++;	//先赋值后++，所以num初始为1.
  		}
  		j -=1; //传给下一个case的j，for循环结束，j = n，所以要减1.
        i +=1; //因为转角元素已经填充，所以↓，不能重复操作转角元素，所以i+1.
        break;

但我想着写成while更好看，所以改变了下：

 case 0:             //方向向右
     while(j <= line){
           matrix[i][j] = num++;   //先赋值后++
            j++;
     }
     j -=1;
     i +=1;
     break;

其余同理完成case填充，每个while结束后调整i,j，都是为了递交下一棒时索引正确。最后大框架得到中间步骤1：

   //每个case内的代码操作填充完毕
   for(int k = 0;k < (2*n-1);k++){
   switch(k % 4){
       case 0:             //方向向右
           while(j <= line){
               matrix[i][j] = num++;   //先赋值后++
               j++;
           }
           j -=1;
           i +=1;
           break;
       case 1:           //方向向下
           while(i <= line){
               matrix[i][j] = num++;
               i++;
           }
           i -=1;	//传给case2，因为while结束，i = n，超出范围，所以减1
           j -=1;    // 转角元素已经操作过。
           break;
       case 2:         //方向向左
           while(j >= row){
               matrix[i][j] = num++;
               j--;
           }
           j +=1;	//while结束后,j=-1，超出下标范围
           i -=1;	//转角元素已经操作过
           break;
       case 3:           //方向向下
           while(i >= row+1){
               matrix[i][j] = num++;
               i--;
           }
           i +=1;
           j +=1;
           break;
       default: break;
   }

while控制范围的条件：line和row变量。

向→或↓步骤：每一轮到这两步时，逐步收缩下标，进入内圈，所以line一轮结束后要减1；
向←或↑步骤，每一轮到这两步时，逐步增加下标，进入内圈，所以row一轮结束后要加1；

所以大框架得到中间步骤2：

//完善for循环中：line和row变量操作—— if(k%4 == 3)

int line = n - 1;		//初始值
int row = 0;			//初始值
int num = 1;  			//填入数字,初始1，不是0
for(int k = 0;k < (2*n-1);k++){
    switch(k % 4){
        case 0:             //方向向右
            while(j <= line){
                matrix[i][j] = num++;   //先赋值后++
                j++;
            }
            j -=1;
            i +=1;
            break;
        case 1:           //方向向下
            while(i <= line){
                matrix[i][j] = num++;
                i++;
            }
            i -=1;
            j -=1;
            break;
        case 2:         //方向向左
            while(j >= row){
                matrix[i][j] = num++;
                j--;
            }
            j +=1;
            i -=1;
            break;
        case 3:           //方向向下
            while(i >= row+1){
                matrix[i][j] = num++;
                i--;
            }
            i +=1;
            j +=1;
            break;
        default: break;
    }     一步
    
    if(k%4 == 3){			//此时要开启新一轮， 下一步是→。收缩到内圈顺时针旋转。
        line--;
        row++;
    }
}

总结：再加上初始化vector二维数组的定义，得到完整代码：

//通过测试，没有问题。
class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> matrix(n,vector<int> (n,0)); //返回值：得到的矩阵
        //for(int i = 0;i < n;i++){          //怎么初始化容器的二维数组？
        //    vector<int> subrow = new int[n]];    //初始化指针，分配内存。
        //    matrix.push_back(subrow);
        //}这个是错误方式初始化。

        int i = 0;//行指针
        int  j = 0;//列指针，操作matrix坐标。

        //控制每轮的范围
        int line = n - 1;
        int row = 0;
        int num = 1;//填入数字,初始1，不是0
        for(int k = 0;k < (2*n-1);k++){
            switch(k % 4){
                case 0:             //方向向右
                    while(j <= line){
                        matrix[i][j] = num++;   //先赋值后++
                        j++;
                    }
                    j -=1;
                    i +=1;
                    break;
                case 1:           //方向向下
                    while(i <= line){
                        matrix[i][j] = num++;
                        i++;
                    }
                    i -=1;
                    j -=1;
                    break;
                case 2:         //方向向左
                    while(j >= row){
                        matrix[i][j] = num++;
                        j--;
                    }
                    j +=1;
                    i -=1;
                    break;
                case 3:           //方向向下
                    while(i >= row+1){
                        matrix[i][j] = num++;
                        i--;
                    }
                    i +=1;
                    j +=1;
                    break;
                default: break;
            }     
            if(k%4 == 3){
                line--;
                row++;
            }
        }
        return matrix;
    }
};

额外补充vector初始化：
1 初始化一维数组：
	vector<int> nums();或vector<int> nums;//创建空容器，没有元素。可以看成一维数组。
	vector<int> nums(n,0);//创建有n个元素的容器，每个元素的值，初始化为0.
2 初始化二维数组：
	vector<int> matrix(n,vector<int> (m,0));//n行m列，元素初始化为0.

三、代码随想录学习

学习内容：

循环不变量：

（1）理解：遇到循环，始终坚持一种区间处理原则，[ )或[ ]或( ]，无论哪种类型都可以，但一定要从头坚持到尾。不可以混合多个区间处理原则，一会一变，就会陷入逻辑混乱。
（2）在【记录一：二分查找】中，同理。

思路对比：

我的思路：虽然发现了循环规律，但是我把每一步单独拆开操作，for循环一次代表下一步：遇到转角元素，要改变方向。所以相对复杂；
卡哥思路：把4步看作一个整体，while循环一次代表完成一圈。更简单。

代码实现：

//靠自己按新思路写一遍,坚持左闭右开区间，即转角元素交给下一条边填充。通过测试。
class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> matrix(n,vector<int> (n,0));//返回值
        int i = 0;  //行坐标
        int j = 0;  //列坐标
        int offset = 0;//每次收缩内圈
        int num = 1;
        int k = 0;
        while(k < n/2){
            for(;j < n - 1-offset;j++){   //没有操作转角元素，留给下一个for
                matrix[i][j] = num++;
            }
            for(;i < n-1-offset;i++){
                matrix[i][j] = num++;
            }
            for(;j > offset;j--){
                matrix[i][j] = num++;
            }
            for(;i > offset;i--){
                matrix[i][j] = num++;
            }
            //收缩内圈
            i++;
            j++;
            offset++;
            k++;
        }
        //n为奇数
        if(n%2){
            matrix[i][j] = num++;
        }
        return matrix;
    }
};

对比参考代码：
1 直接用i ,j 操作元素，相当于startx和starty，所以可以不要startx和starty。
2 我用k控制循环次数，多了两行代码：int k = 0;k++;
	但参考直接loop--即可。（采纳）

另外我想再写一个区间是左开右闭，即转角元素交给当前边填充：（也就是第一次尝试的思路）

注意：第四个for没有“=”，而且第一个for开始需要特别处理起始元素。所以比左闭右开麻烦一些，需要注意边界。

//通过测试。左开右闭，即转角元素交给当前边填充。特别处理起始元素。
class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> matrix(n,vector<int> (n,0));
        int i = 0;//横坐标
        int j =0;//纵坐标
        int offset = 0;//收缩内圈
        int loop = n/2;//循环圈数
        int mid = n/2; //正中间的元素
        int num = 1;//填充元素
        while(loop--){
            matrix[i][j] = num++;   //起始元素处理
            for(j = j+1;j <= n-1-offset;j++){
                matrix[i][j] = num++;
            }
            for(i = i+1,j=j-1;i <= n-1-offset;i++){
                matrix[i][j] = num++;
            }
            for(j=j-1,i=i-1; j >= offset;j--){
                matrix[i][j] = num++;
            }
            for(i=i-1,j=j+1;i > offset;i--){    //注意没有“=”
                matrix[i][j] = num++;
            }
            i++;
            j++;
            offset++;
        }
        if(n%2){
            matrix[mid][mid] = num++;
        }
        return matrix;


    }
};

总结

反思

（1）我发现了规律，想到了循环，但是没有看作一个整体，而是一步一步的划分开。所以操作麻烦，每次都要修正i,j坐标。但是按照参考思路，每个while完成一圈就很方便。

收获

通过控制i,j，始终坚持循环不变量，遵循从一而终的区间原则，通过本文可以掌握较好。

（欢迎指正，转载标明出处）