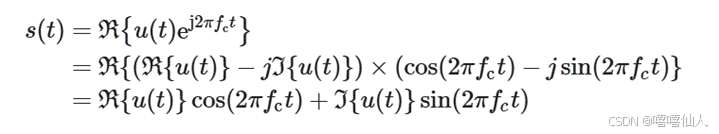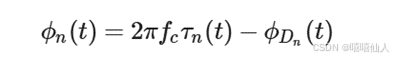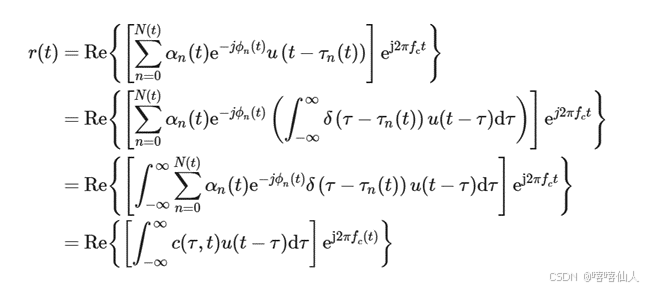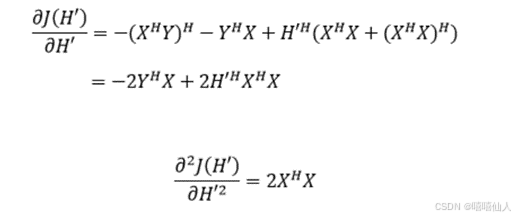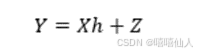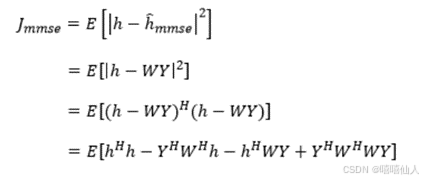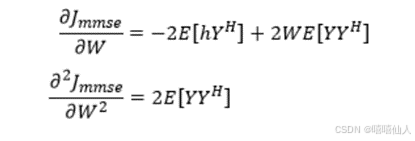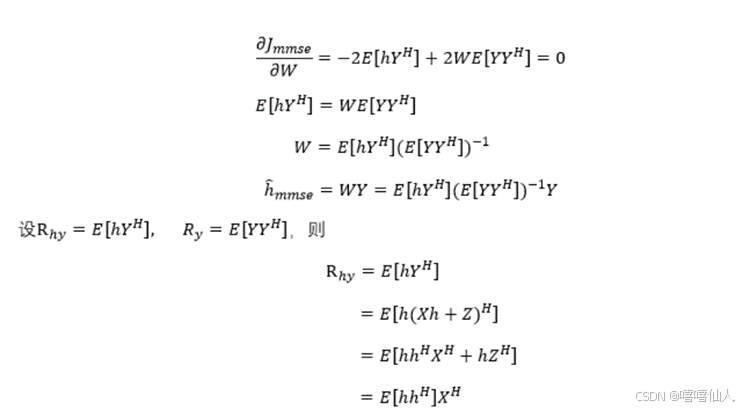本文是XDU随机信号课程的大作业,因为笔者之前只是浅显的接触过信道估计的概念,所以借此机会查阅了一些资料并进行了一些MATLAB的仿真实验加深理解。由于涉猎不深,请读者仅供参考,如有错误也欢迎各位大佬在评论区讨论指正~
一. 背景引入
在所有的通信过程中,从输入端到输出端,都要经过一定的介质(通道),当信号通过这些通道时,信号会发生衰减、相移、失真等变化,还会有噪声加入,要想在将输出的信号正确解码而且没有太多的错误,我们就需要从接收的信号中删除信道对于信号施加的影响。为此,第一步是找出信号经过的信道的特征,这就是信道估计。
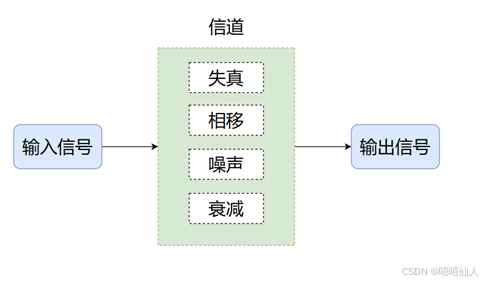
如果信道是线性的话,那么信道估计就是对系统冲激响应进行估计。需强调的是信道估计是信道对输入信号影响的一种数学表示,而“好”的信道估计则是使得某种估计误差最小化的估计算法。通过信道估计,接收机可以得到信道的冲激响应,从而为后续的相干解调提供所需的信道状态信息。一个良好的估计和均衡算法对于接收端的性能至关重要,决定了信号最终的的解出率。
二. 实验原理
1. 信道估计的基本流程如下:
(1)建立信道矩阵的模型,将输入信号和输出信号关联起来
(2)一端输入传输信号,输出端检测信号
(3)通过比较传输的信号和接收到的信号,找出信道矩阵中的元素
2. 信道估计的基本思想如下:
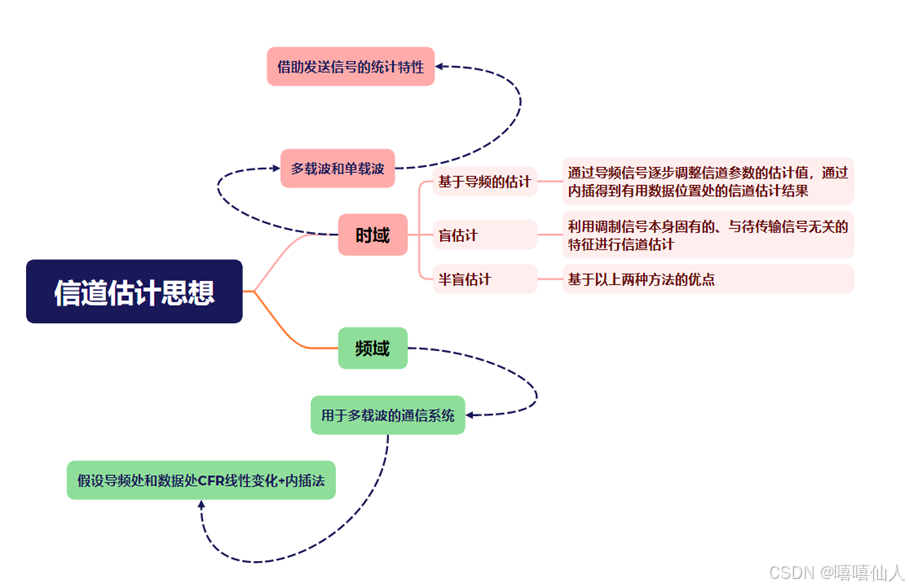
3. 多径信道的产生原理:
当通信环境比较复杂时,信号在接收端会由多个信号副本组成,假设要发送的基带信号u(t),通过将发送信号与高频载波相乘,并取结果的实部,即为发送端最终发送的信号。乘载波的过程可以表示为:
该信号的多个副本经过不同传播路径后在接收端叠加,叠加后信号可以表示为:
是不同路径信号幅度时变衰减,由路径损耗和阴影衰落确定;
是不同路径的信号路径传输时延
,
是不同路径的多谱勒相移。从上式可以看出,相比于原始信号,第
路多径信号的相位变化量为:
上式可以转换成输入信号和信道响应相互卷积的形式
直观地来理解一下上面的卷积形式的接收信号:对于任意的发射时刻都有可能对
时刻的接收信号产生贡献。但是究竟是哪几个时刻发射信号会产生贡献和产生什么样的贡献呢?
回答了这个问题,通过与
卷积,确定了发射时刻和接受时刻的时间差等于路径传输时延的信号,并赋予了幅度衰减和相位变化。
表示
时刻发出的信号,在时刻收到,此时信号对应的信道系数。
体现了时变信道的两个特点: 1. 通信时间不同(t不同),对应信道状态不同 2. 传播延时不同
不同),对应信道状态不同。在最简化的情况下,信道响应不随时间发生变化,这样一来信道响应就只与多径时延有关,即
4. 信道估计的方法
信道估计的方法有很多种,大体上可分为两类,一类是基于训练序列的信道估计,而另一类是信道的盲估计(自适应估计),其估计过程不依赖已知信息。常见通信系统的信道估计,绝大部分是基于训练序列的估计方法,这里面最最常用的两个信道估计算法就是LS算法和MMSE算法。LS是最小二乘、MMSE是最小均方误差,它们都是所谓的最优化准则,即得到最优信道估计所遵循的准则,有时也被称为代价函数。
(1)最小二乘法信道估计算法(LS)
建立如下信号关系式:
其中Y为实际接收数据,Y’为估计的接收数据,其大小均为N1X1的矩阵(N1为参与LSCE计算的数据数量),Z 为噪声也是一个N1X1的矩阵,H是真实信道矩阵,H’是估计信道矩阵,大小为N2X1(N2为估计的多径数量)。X为发送数据矩阵,是一个N1XN2的矩阵,其包含的数据为按行进行符号延迟的数据。
依据LS最优准则对上式中H’进行估计,首先给出LS准则的代价函数:
上式中的H’就是LS信道估计的结果,可见其计算过程需要对X的自相关矩阵进行求逆运算,在实际使用中,因为X矩阵是已知的,因此XHX的逆矩阵可以提前计算出来,而不用在代码实现中再进行求逆运算,从而简化计算过程。LS信道估计使用的优化准则为:实际接收数据(实际观测量)与估计的接收数据(估计观测量)之间的误差平方和最小。这就造成了估计出来的信道矩阵与实际的信道矩阵存在一定误差,而且这个误差会随着信噪比的降低越来越大,这也是为什么LS信道估计不适合应用在信噪比较低的场景中。
最小二乘法信道估计算法(LS)仿真

% 初始化参数
N = 100; % 样本数量
sigma = 0.1; % 信道噪声方差
% 生成信道h
h = sqrt(sigma) * (randn(1, N) + 1j * randn(1, N));
% 生成导频信号x
k = 1:N;
M1 = 1;
x = exp((1j * pi * M1 * k.^2) / N).';
% 生成噪声nt
nt = sqrt(sigma) * (randn(1, N) + 1j * randn(1, N));
% 构造接收信号y
y = h .* x + nt;
% LS法信道估计
h_est = y ./ x;
% 输出信号的构造
t = linspace(0, 2*pi, N);
input_signal = 8 * sin(5*t + 8);
output_signal = 3 * sin(5*t + 10);
% 下采样因子
downsample_factor = 5;
% 下采样索引
indices = 1:downsample_factor:N;
% 确保索引不超过向量长度
if indices(end) > N
indices = indices(1:end-1);
end
% 绘制结果
figure;
subplot(3, 1, 1);
plot(indices, abs(h(indices)), 'b', 'LineWidth', 2);
hold on;
plot(indices, abs(h_est(indices)), 'r--', 'LineWidth', 2);
legend('真实信道h', '估计信道h\_est');
title('信道幅度对比');
xlabel('样本点');
ylabel('幅度');
grid on;
subplot(3, 1, 2);
plot(indices, angle(h(indices)), 'b', 'LineWidth', 2);
hold on;
plot(indices, angle(h_est(indices)), 'r--', 'LineWidth', 2);
legend('真实信道h', '估计信道h\_est');
title('信道相位对比');
xlabel('样本点');
ylabel('相位');
grid on;
subplot(3, 1, 3);
plot(t(indices), input_signal(indices), 'b', 'LineWidth', 2);
hold on;
plot(t(indices), output_signal(indices), 'r--', 'LineWidth', 2);
legend('输入信号', '输出信号');
title('输入输出信号对比');
xlabel('时间');
ylabel('信号幅度');
grid on;

通过观察仿真图可知,估计信道与真实信道存在着较大的差距。这是因为在LS估计中,我们使用Y和Y‘’来进行计算,估计出的结果是H’而并非H,若估计的结果H’使得Y’与Y误差最小,则能得到的结果应该是H’与H(带三角)的误差最小,但H(带三角)也不是真实的信道矩阵,其内还包含了一个误差项Z/X,因此对于LS信道估计而言,其结果的精度是受这个误差项影响的。
当改变增大噪声的方差以此来减小信噪比,仿真结果如下:


可以发现估计信道和真实信道之间的误差更大,论证了LS信道估计法不适用于信噪比低的环境下。
(2)最小均方信道估计算法(MMSE)
LS算法使用的是实际观测量与估计观测量的误差,这并不能精确的代表估计量的真值与估计值的误差,因此在MMSE估计算法中,直接使用估计量真值与估计值的误差,作为优化的目标。这样就将噪声的影响消除掉了,因此能得到比LS估计更精确的估计值。
给出假定的信号关系式
Y为接收数据(包含多径)大小为Nx1。X为先验信息,大小为NXM。h为信道冲激响应,大小为MX1。Z为噪声,大小为NX1。MMSE信道估计的代价函数为:
MMSE信道估计的计算,用到了LS信道估计的结果,并且还需要知道信道相关矩阵Rh以及信道噪声的平均功率σ2,才能进行计算,计算式中有两个矩阵求逆运算,可见其计算量比较巨大,不太适合直接计算。信道相关矩阵Rh以及信道噪声的平均功率σ2,都可通过LS估计的结果得到。
最小均方信道估计算法(MMSE)仿真

% 初始化参数
N = 100; % 样本数量
sigma = 0.1; % 信道噪声方差
SNR = 10; % 信噪比(线性值)
% 生成信道h
h = sqrt(sigma) * (randn(1, N) + 1j * randn(1, N));
% 生成导频信号x
k = 1:N;
M1 = 1;
x = exp((1j * pi * M1 * k.^2) / N).';
% 生成噪声nt
nt = sqrt(sigma) * (randn(1, N) + 1j * randn(1, N));
% 构造接收信号y
y = h .* x + nt;
% 信号和噪声功率
P_signal = mean(abs(x).^2);
P_noise = sigma;
% MMSE法信道估计
h_mmse = (conj(x) .* y) ./ (abs(x).^2 + P_noise/P_signal);
% 输出信号的构造
t = linspace(0, 2*pi, N);
input_signal = 8 * sin(5*t + 8);
output_signal = 3 * sin(5*t + 10);
% 下采样因子
downsample_factor = 5;
% 下采样索引
indices = 1:downsample_factor:N;
% 确保索引不超过向量长度
if indices(end) > N
indices = indices(1:end-1);
end
% 绘制结果
figure;
subplot(3, 1, 1);
plot(indices, abs(h(indices)), 'b', 'LineWidth', 2);
hold on;
plot(indices, abs(h_mmse(indices)), 'r--', 'LineWidth', 2);
legend('真实信道h', '估计信道h\_mmse');
title('信道幅度对比');
xlabel('样本点');
ylabel('幅度');
grid on;
subplot(3, 1, 2);
plot(indices, angle(h(indices)), 'b', 'LineWidth', 2);
hold on;
plot(indices, angle(h_mmse(indices)), 'r--', 'LineWidth', 2);
legend('真实信道h', '估计信道h\_mmse');
title('信道相位对比');
xlabel('样本点');
ylabel('相位');
grid on;
subplot(3, 1, 3);
plot(t(indices), input_signal(indices), 'b', 'LineWidth', 2);
hold on;
plot(t(indices), output_signal(indices), 'r--', 'LineWidth', 2);
legend('输入信号', '输出信号');
title('输入输出信号对比');
xlabel('时间');
ylabel('信号幅度');
grid on;
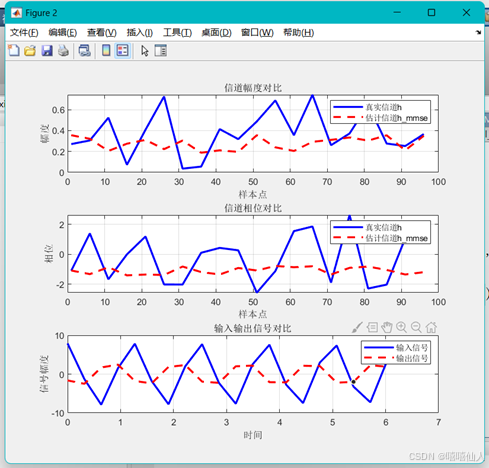
(3)LMMSE信道估计
LMMSE信道估计方法,相对于MMSE估计,它在不损失太多性能的前提下,降低了计算的复杂度,因此大部分的实际系统中,实用的就是这个估计方法。
将MMSE计算公式中的XHX用其均值来代替,即:
LMMSE估计比MMSE估计省掉了一个矩阵求逆过程,实际工程中,还是有诸如SVD分解等其他的方法来进一步降低LMMSE的计算量 。
三. 实验过程
(1)LS信道估计方法
% 参数初始化
N = 100; % 样本数
sigma = 0.5; % 噪声方差
SNR_dB = -5:5:30; % 信噪比范围,单位为dB
numSNR = length(SNR_dB); % 信噪比数量
% 生成信道 h
h = sqrt(sigma) * (randn(1, N) + 1j * randn(1, N));
% 生成导频信号 x
k = 1:N;
M1 = 1;
x = exp((1j * pi * M1 * k.^2) / N).';
% 生成噪声
nt = sqrt(sigma/2) * (randn(N, numSNR) + 1j * randn(N, numSNR));
% 初始化变量以存储结果
h_est = zeros(N, numSNR);
mean_distance = zeros(1, numSNR);
h_magnitude = zeros(N, numSNR);
h_phase = zeros(N, numSNR);
h_est_magnitude = zeros(N, numSNR);
h_est_phase = zeros(N, numSNR);
for idx = 1:numSNR
% 计算线性信噪比
SNR_linear = 10^(SNR_dB(idx) / 10);
% 计算噪声功率
noise_power = sigma / SNR_linear;
% 生成噪声
noise = sqrt(noise_power / 2) * (randn(N, 1) + 1j * randn(N, 1));
% 生成接收信号 y
y = h.' .* x + noise;
% LS 信道估计
h_est(:, idx) = y ./ x;
% 计算误差
real_diff = real(h) - real(h_est(:, idx)).';
imag_diff = imag(h) - imag(h_est(:, idx)).';
mean_distance(idx) = mean(sqrt(real_diff.^2 + imag_diff.^2));
% 幅值和相位
h_magnitude(:, idx) = abs(h);
h_phase(:, idx) = angle(h);
h_est_magnitude(:, idx) = abs(h_est(:, idx));
h_est_phase(:, idx) = angle(h_est(:, idx));
end
% 绘制平均距离与信噪比的关系
figure;
plot(SNR_dB, mean_distance, '-o');
xlabel('SNR (dB)');
ylabel('Mean Distance');
title('估计值与真实值之间的平均距离');
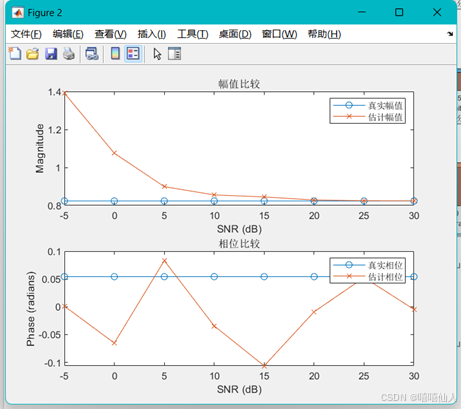
% 幅值比较
figure;
subplot(2,1,1);
plot(SNR_dB, mean(h_magnitude, 1), '-o');
hold on;
plot(SNR_dB, mean(h_est_magnitude, 1), '-x');
xlabel('SNR (dB)');
ylabel('Magnitude');
title('幅值比较');
legend('真实幅值', '估计幅值');
% 相位比较
subplot(2,1,2);
plot(SNR_dB, mean(h_phase, 1), '-o');
hold on;
plot(SNR_dB, mean(h_est_phase, 1), '-x');
xlabel('SNR (dB)');
ylabel('Phase (radians)');
title('相位比较');
legend('真实相位', '估计相位');
% 分析幅值和相位的分布
figure;
subplot(2,1,1);
histogram(h_magnitude(:), 'Normalization', 'pdf');
hold on;
histogram(h_est_magnitude(:), 'Normalization', 'pdf');
xlabel('Magnitude');
ylabel('Probability Density');
title('幅值分布');
legend('真实幅值', '估计幅值');
subplot(2,1,2);
histogram(h_phase(:), 'Normalization', 'pdf');
hold on;
histogram(h_est_phase(:), 'Normalization', 'pdf');
xlabel('Phase (radians)');
ylabel('Probability Density');
title('相位分布');
legend('真实相位', '估计相位');
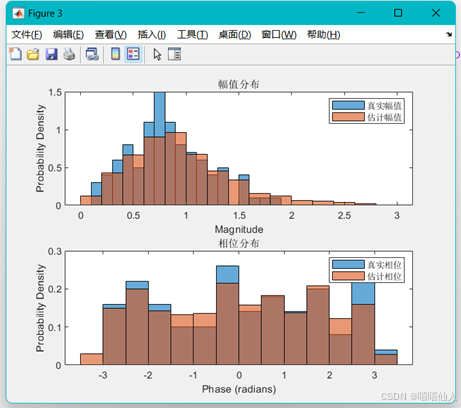

(2)MMSE信道估计
clear all
% 参数初始化
N = 100; % 样本数
sigma = 0.5; % 噪声方差
SNR_dB = -10:5:30; % 信噪比范围,单位为dB
numSNR = length(SNR_dB); % 信噪比数量
% 生成信道 h
h = sqrt(sigma) * (randn(1, N) + 1j * randn(1, N));
% 生成导频信号 x
k = 1:N;
M1 = 1;
x = exp((1j * pi * M1 * k.^2) / N).';
% 噪声生成
nt = sqrt(sigma/2) * (randn(N, numSNR) + 1j * randn(N, numSNR));
% 初始化变量以存储结果
h_est = zeros(N, numSNR);
mean_distance = zeros(1, numSNR);
h_magnitude = zeros(N, numSNR);
h_phase = zeros(N, numSNR);
h_est_magnitude = zeros(N, numSNR);
h_est_phase = zeros(N, numSNR);
% 导频信号的协方差矩阵
Rxx = x * x';
for idx = 1:numSNR
% 计算线性信噪比
SNR_linear = 10^(SNR_dB(idx) / 10);
% 计算噪声功率
noise_power = sigma / SNR_linear;
% 生成噪声
noise = sqrt(noise_power / 2) * (randn(N, 1) + 1j * randn(N, 1));
% 生成接收信号 y
y = h.' .* x + noise;
% MMSE 信道估计
Ryy = Rxx + noise_power * eye(N); % 接收信号协方差矩阵
h_est(:, idx) = (Rxx / Ryy) * y; % MMSE估计公式
% 计算误差
real_diff = real(h) - real(h_est(:, idx)).';
imag_diff = imag(h) - imag(h_est(:, idx)).';
mean_distance(idx) = mean(sqrt(real_diff.^2 + imag_diff.^2));
% 幅值和相位
h_magnitude(:, idx) = abs(h);
h_phase(:, idx) = angle(h);
h_est_magnitude(:, idx) = abs(h_est(:, idx));
h_est_phase(:, idx) = angle(h_est(:, idx));
end
% 绘制平均距离与信噪比的关系
figure;
plot(SNR_dB, mean_distance, '-o');
xlabel('SNR (dB)');
ylabel('Mean Distance');
title('估计值与真实值之间的平均距离');
% 幅值比较
figure;
subplot(2,1,1);
plot(SNR_dB, mean(h_magnitude, 1), '-o');
hold on;
plot(SNR_dB, mean(h_est_magnitude, 1), '-x');
xlabel('SNR (dB)');
ylabel('Magnitude');
title('幅值比较');
legend('真实幅值', '估计幅值');
% 相位比较
subplot(2,1,2);
plot(SNR_dB, mean(h_phase, 1), '-o');
hold on;
plot(SNR_dB, mean(h_est_phase, 1), '-x');
xlabel('SNR (dB)');
ylabel('Phase (radians)');
title('相位比较');
legend('真实相位', '估计相位');
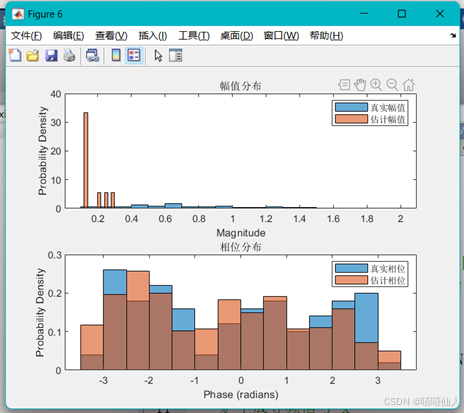
% 分析幅值和相位的分布
figure;
subplot(2,1,1);
histogram(h_magnitude(:), 'Normalization', 'pdf');
hold on;
histogram(h_est_magnitude(:), 'Normalization', 'pdf');
xlabel('Magnitude');
ylabel('Probability Density');
title('幅值分布');
legend('真实幅值', '估计幅值');
subplot(2,1,2);
histogram(h_phase(:), 'Normalization', 'pdf');
hold on;
histogram(h_est_phase(:), 'Normalization', 'pdf');
xlabel('Phase (radians)');
ylabel('Probability Density');
title('相位分布');
legend('真实相位', '估计相位');


(3)LS估计和MMSE估计的比较
clear all
% 参数初始化
N = 100; % 样本数
sigma = 0.5; % 噪声方差
SNR_dB = 20:5:60; % 信噪比范围,单位为dB
numSNR = length(SNR_dB); % 信噪比数量
% 生成信道 h
h = sqrt(sigma) * (randn(1, N) + 1j * randn(1, N));
% 生成导频信号 x
k = 1:N;
M1 = 1;
x = exp((1j * pi * M1 * k.^2) / N).';
% 噪声生成
nt = sqrt(sigma/2) * (randn(N, numSNR) + 1j * randn(N, numSNR));
% 初始化变量以存储结果
h_est_ls = zeros(N, numSNR);
h_est_mmse = zeros(N, numSNR);
mean_distance_ls = zeros(1, numSNR);
mean_distance_mmse = zeros(1, numSNR);
% 导频信号的协方差矩阵
Rxx = x * x';
for idx = 1:numSNR
% 计算线性信噪比
SNR_linear = 10^(SNR_dB(idx) / 10);
% 计算噪声功率
noise_power = sigma / SNR_linear;
% 生成噪声
noise = sqrt(noise_power / 2) * (randn(N, 1) + 1j * randn(N, 1));
% 生成接收信号 y
y = h.' .* x + noise;
% LS 信道估计
h_est_ls(:, idx) = y ./ x;
% MMSE 信道估计
Ryy = Rxx + noise_power * eye(N); % 接收信号协方差矩阵
h_est_mmse(:, idx) = (Rxx / Ryy) * y; % MMSE估计公式
% 计算LS估计误差
real_diff_ls = real(h) - real(h_est_ls(:, idx)).';
imag_diff_ls = imag(h) - imag(h_est_ls(:, idx)).';
mean_distance_ls(idx) = mean(sqrt(real_diff_ls.^2 + imag_diff_ls.^2));
% 计算MMSE估计误差
real_diff_mmse = real(h) - real(h_est_mmse(:, idx)).';
imag_diff_mmse = imag(h) - imag(h_est_mmse(:, idx)).';
mean_distance_mmse(idx) = mean(sqrt(real_diff_mmse.^2 + imag_diff_mmse.^2));
end
% 绘制平均距离与信噪比的关系
figure;
plot(SNR_dB, mean_distance_ls, '-o');
hold on;
plot(SNR_dB, mean_distance_mmse, '-x');
xlabel('SNR (dB)');
ylabel('Mean Distance');
title('估计值与真实值之间的平均距离');
legend('LS 估计', 'MMSE 估计');
% 幅值比较
figure;
subplot(2,1,1);
plot(SNR_dB, mean(abs(h)), '-o');
hold on;
plot(SNR_dB, mean(abs(h_est_ls)), '-x');
plot(SNR_dB, mean(abs(h_est_mmse)), '-^');
xlabel('SNR (dB)');
ylabel('Magnitude');
title('幅值比较');
legend('真实幅值', 'LS 估计幅值', 'MMSE 估计幅值');
% 相位比较
subplot(2,1,2);
plot(SNR_dB, mean(angle(h)), '-o');
hold on;
plot(SNR_dB, mean(angle(h_est_ls)), '-x');
plot(SNR_dB, mean(angle(h_est_mmse)), '-^');
xlabel('SNR (dB)');
ylabel('Phase (radians)');
title('相位比较');
legend('真实相位', 'LS 估计相位', 'MMSE 估计相位');
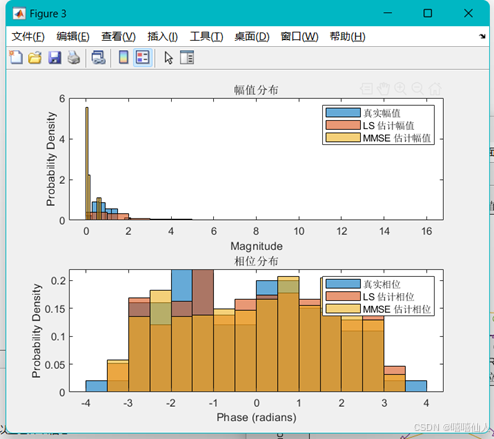
% 分析幅值和相位的分布
figure;
subplot(2,1,1);
histogram(abs(h), 'Normalization', 'pdf');
hold on;
histogram(abs(h_est_ls(:)), 'Normalization', 'pdf');
histogram(abs(h_est_mmse(:)), 'Normalization', 'pdf');
xlabel('Magnitude');
ylabel('Probability Density');
title('幅值分布');
legend('真实幅值', 'LS 估计幅值', 'MMSE 估计幅值');
subplot(2,1,2);
histogram(angle(h), 'Normalization', 'pdf');
hold on;
histogram(angle(h_est_ls(:)), 'Normalization', 'pdf');
histogram(angle(h_est_mmse(:)), 'Normalization', 'pdf');
xlabel('Phase (radians)');
ylabel('Probability Density');
title('相位分布');
legend('真实相位', 'LS 估计相位', 'MMSE 估计相位');

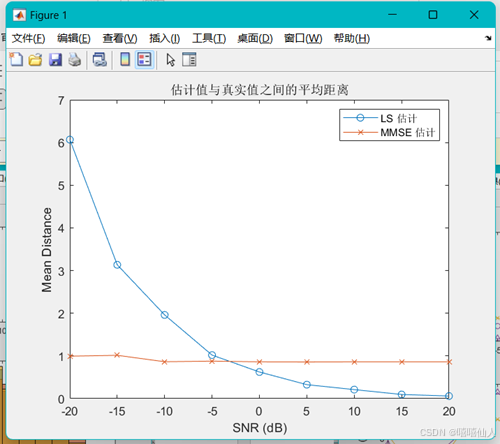

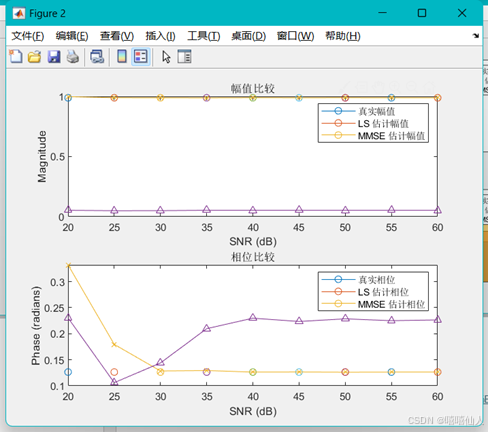
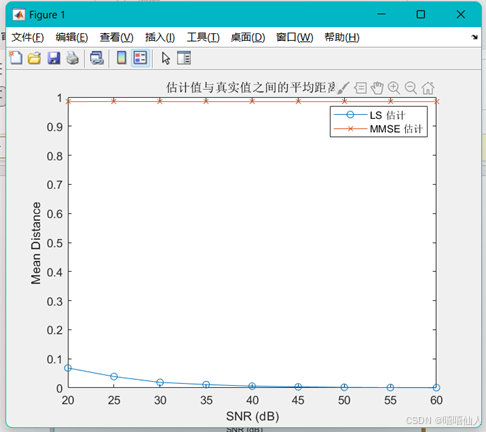
1. 估计误差: 从图形可以看出,在高信噪比条件下,MMSE估计的误差通常小于LS估计的误差,因为MMSE估计充分利用了信道和噪声的统计特性,具有更好的性能。
2. 幅值和相位估计: MMSE估计在高信噪比下的幅值和相位估计也比LS估计更接近真实值。
3. 噪声影响: 在低信噪比条件下,噪声对估计性能的影响较大,MMSE估计仍能比LS估计提供更可靠的结果。
五. 参考文献
https://blog.csdn.net/qq_36554582/article/details/108918657
https://www.cnblogs.com/louisanu/p/13046621.html