【信息论基础第七讲】离散无记忆信源不等长编码

我们在上一讲说道码字长度相等的情况下称为等长编码，而我们根据信源符号出现的概率大小可以对其进行不等长编码。

最常见的不等长编码的例子就是摩尔斯电码，莫尔斯电码都是用点和划组成。我们规定点用“1”表示，划用“111”表示，相邻的点或者划之间用“0”隔开，每个字母的结束用“000”标识。

例如对于字母“E”，在莫尔斯电码中是“点”，那么根据上述的编码规则，“E”对应的是1000；对于字母“J”，在莫尔斯电码中是“点划划划”，“J”对应的是1011101110111000。观察E和J的编码可以发现，其编码长度不同，这就是所谓的不等长编码，为什么会出现E短J长的结果呢？其实在英文中E要比J出现的概率更大，经常出现的字母就变换为较短的数字序列，不经常出现的字母就变换为较长的数字序列。

一、平均码长

我们使用平均码长来衡量编码的效率，我们希望平均码长尽可能得小。概率大的事件用短字码就可以实现。

二、不等长码的唯一可译性

1、条件

对于等长码而言，如果接收端收到一串序列，每个码字的长度相等，将受到的序列按照此长度进行划分，再根据译码表进行译码即可、

但是对于不等长码而言，要想保证唯一可译性，首先要保证每个消息都至少有一个码字与之对应，且不同的消息对应不同的码字；其次因为不能根据长度划分，要想知道在一串序列中一个消息对应的码的起始位置必须要保证码字的分点唯一确定，不能有不同的划分方法否则无法保证唯一可译性。

2、唯一可译的两种解决方法

（1）逗点码

见到逗号就识别为一个码字的开始，每个码字的开头部分都是一个相同的字母串。比如0,01,011,0111。

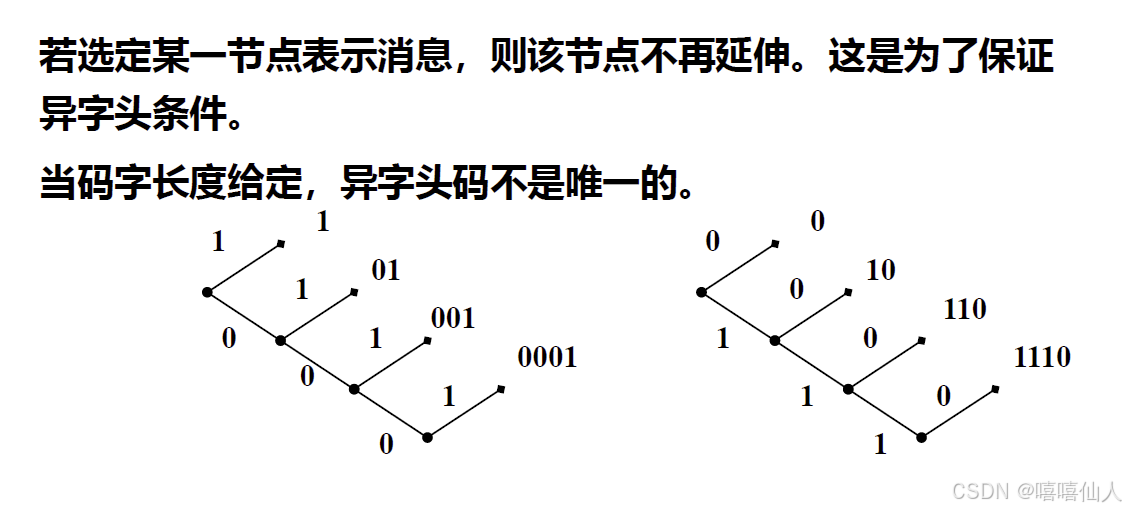
（2）异字头码

见到一个码字就立即识别，每个码字都不是另一个码字的开头部分。比如0,10，110,111。

我们计算上述逗点码和异字头码的平均码长，发现异字头码的平均码长小于逗点码，说明异字头码的编码性能要跟好一些。除此之外，异字头码还有一些其他很好的性质。

（i）显而易见异字头码是唯一可译码

（ii）异字头码具有即时性

这一性质是相对于逗点码而言的，对于逗点码就不满足即时性，因为他的开头都相似，我不能见到一个码字就贸然识别，而对于异字头码而言，头部都不同，因此具有唯一性，所以我只要一见到码字就可以即刻识别。这一特点相比于逗点码在数据量很大时可以减少时延，降低存储负担。

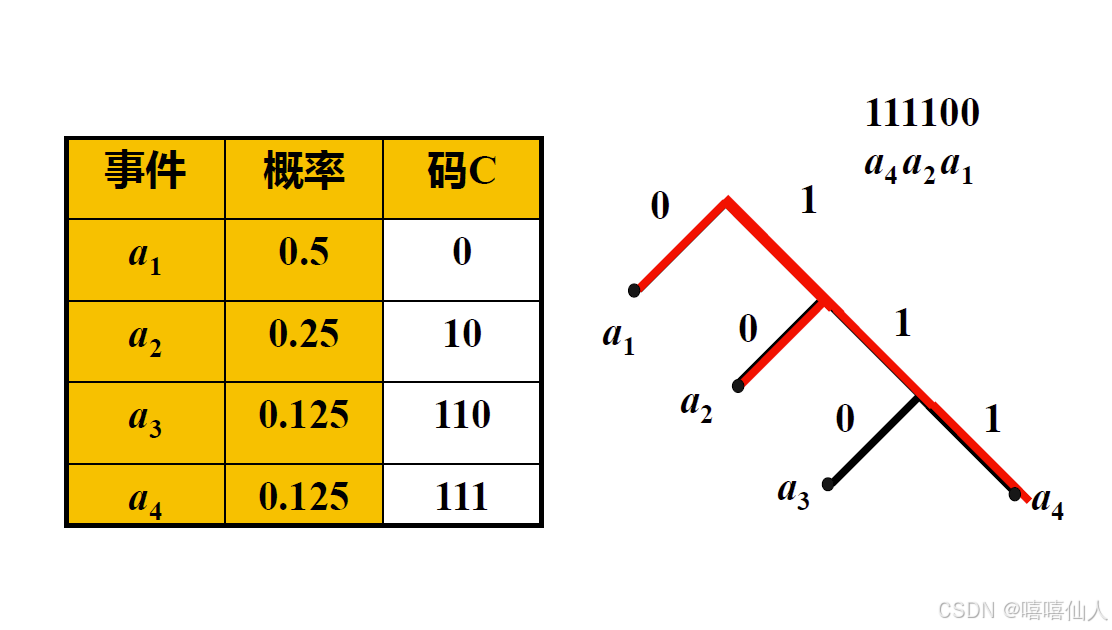
（iii）异字头码可以通过树图表示

异字头码的译码：

异字头码的编码：

但是我们发现并不是能够构造出K个码字，码长分别为n1,n2...nk的D元异字头码。

我们需要Kraft不等式的约束：

这里需要注意的是：Kraft不等式是用来判断D元异字头码存在的充要条件，而不是判断一个码是不是唯一可译码的判据。

我们可以结合码树对Kraft不等式进行说明，设有一个异字头码存在，它的各个码字长度为n1≤n2≤...nk，则可以作为一个nk级满树，则n1级节点中任何一个作为端点占去了满树种所有可能nk级节点的D的（nk-n1）次方/D的（nk）次方=D的（-n1），依次进行下去，当为第K个消息选择码字时，这K个码字至多覆盖整个码数，即满足Craft不等式。

（3）唯一可译码必要条件

定理：唯一可译码必须满足Kraft不等式

定理：长度分别为n1、n2...nk的D元异字头码存在的充分必要条件是Craft不等式

结合上述两个定理可知：任一满足Kraft不等式的非异字头码都可以找到一个码字长度不变的异字头码替代之。