一、复数的修仙之路
在引入欧拉公式之前,我们先思考这样一个问题:为什么会有复数呢?
在笔者的记忆里,复数好像是高中时候的天外来物,突然出现在了数学课本和试卷上,而复数的题目往往是高考试卷的简单题,但是到了大学接触到了一些诸如电磁场和信号与系统这些学科,复数的回旋镖正中眉心,之前老师也妹说复数这么有说法啊......
其实仔细想想早在初中的时候复数就已经犹抱琵琶半遮面了,我们在求解一元二次方程时候,需要通过(b^2-4ac)来判断方程有没有实数根。
在解二次方程时,孩子们有可能会遇到根号里面有一个负数的情况,但是老师说,不用管它我们就认定它无实数解即可,当时,好奇的同学就会问到:负数不能开方吗?
老师往往会说,只有正数和零才有平方根(其实很多教辅和教材都是这样给出了),没有哪个数字自己乘以自己会等于负数。
这个事情也许就不了了之了。
后来,意大利数学家、工程师拉斐尔·邦贝利(Bombelli,Rafael,1528~1572)在16世纪60年代提出有时候需要负数的平方根才能找到真正的解,不过他依然没有将如上题目所得结果中的内容看做一类数,而是称之为“新型方根”。
半个世纪后,笛卡尔似乎发现了,只要允许“不真的、想象的”、“无用的根”,(以上所说的其实就是虚根),那么n次方程会有n个根。
这时候,就有个伟大的法国裔英国籍的数学家亚伯拉罕·棣莫弗(Abraham De Moivre)站了出来,大手一挥给了一个公式:
[cosx+isinx]^n=cosnx+isinnx
这个著名的公式在数年后,由天才数学家欧拉用公式:
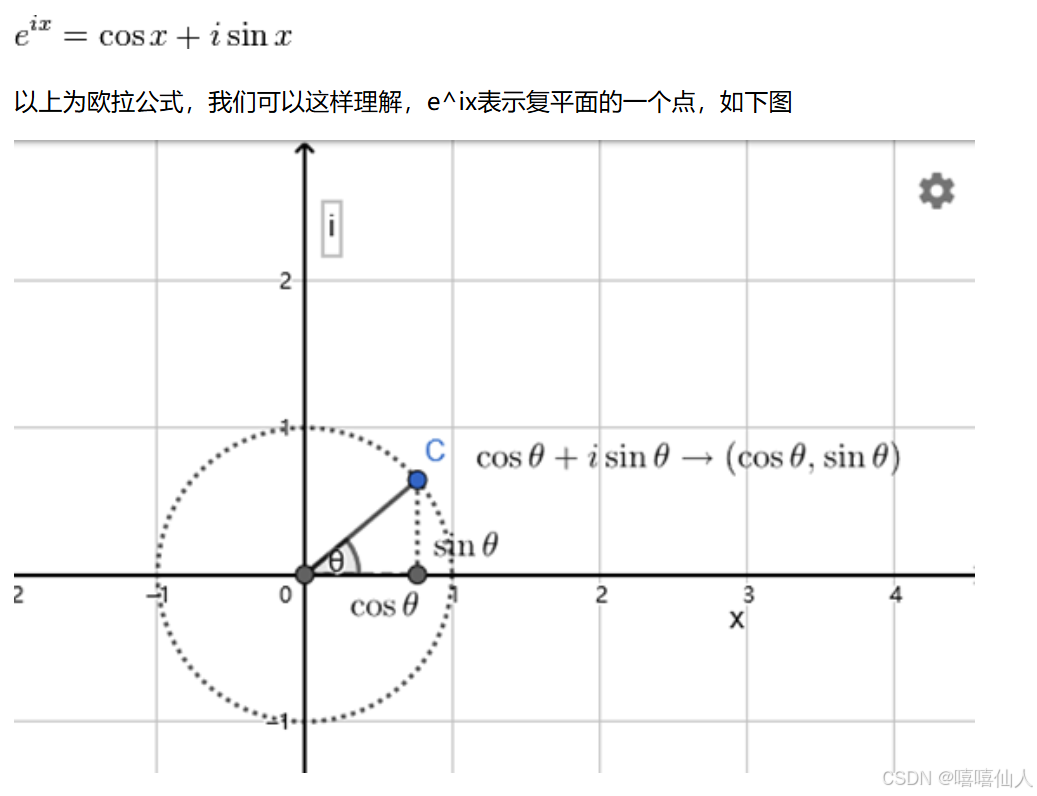
e^(ix)=(cos x+isin x)
将以上公式都进行了统一。
特别的还有:
e^(iπ)=-1
或:e^(iπ)+1=0
不过欧拉大量使用复数,可是并没有解决他们实际上是什么问题。也就是说复数是极其有用的虚构。
在19世纪,复数这个概念逐渐才开始理出了头绪,罗贝尔·阿尔冈(1768-1822)在自己出版的一本数学著作里,提到了用平面几何方法消除“虚构”的虚数的神秘,尽管它们最先是挪威-丹麦土地测量员和数学家卡斯帕尔·韦塞尔(1745-1818)叙述的。阿尔冈对两个复数的加法研究,是符合平行四边形法则的向量加法定律的;乘法是对应于复数的“旋转和缩放”,为了纪念阿尔冈在这方面的突出贡献,都称该复平面为阿尔冈复平面。
到1831年数学王子高斯提出了许多类似或几乎相同的想法并指出这非常有用,并以“复数”来命名,而且指出其是包含多个成分的一个数:有实部,有虚部。
后来经过爱尔兰数学家、物理学家哈密尔顿(1805~1865)证明,可以将复数与平面中的有序数对进行对应。
由柯西、高斯等数学天才们设计了复数微积分,在黎曼、魏尔斯特拉斯等人的手里,将其更是变成了倚天剑屠龙刀般的存在。
至此,复数的产生过程算是完成了。
二、欧拉公式的图形之美
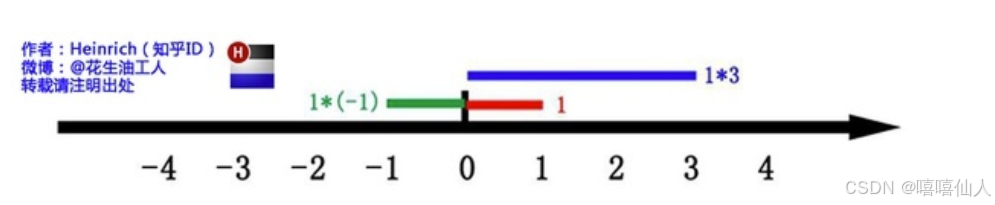
这里有一条数轴,在数轴上有一个红色的线段,它的长度是1。当它乘以 3 的时候,它的长度发生了变化,变成了蓝色的线段,而当它乘以-1 的时候,就变成了绿色的线段,或者说线段在数轴上围绕原点旋转了 180 度。
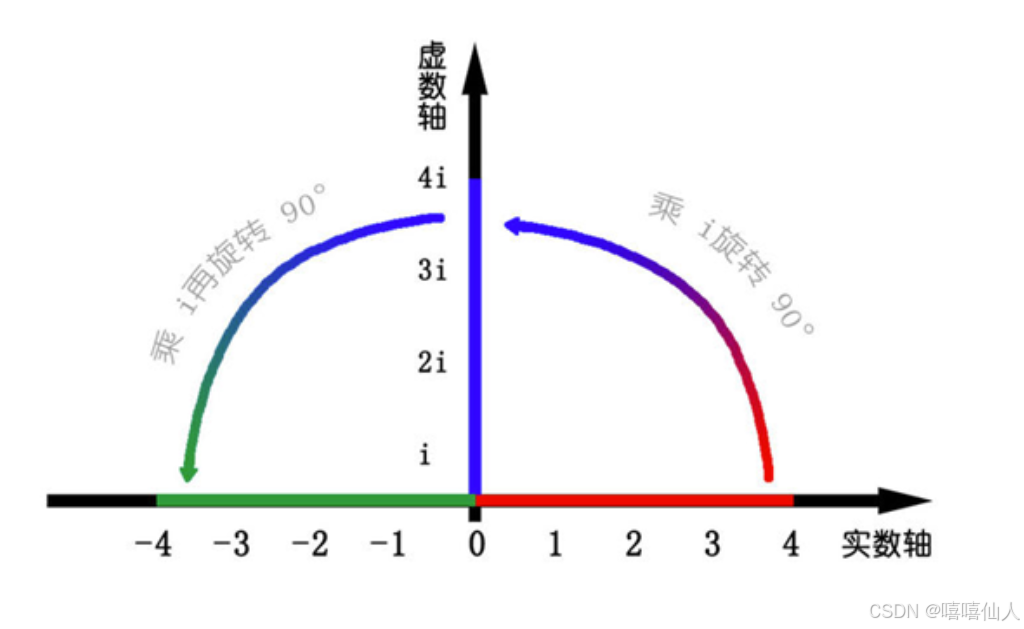
我们知道乘-1 其实就是乘了两次 i 使线段旋转了 180 度,那么乘一次 i 呢——答案很简单——旋转了 90 度。
同时,我们获得了一个垂直的虚数轴。实数轴与虚数轴共同构成了一个复数的平面,也称复平面。这样我们就了解到,乘虚数i的一个功能——旋转。
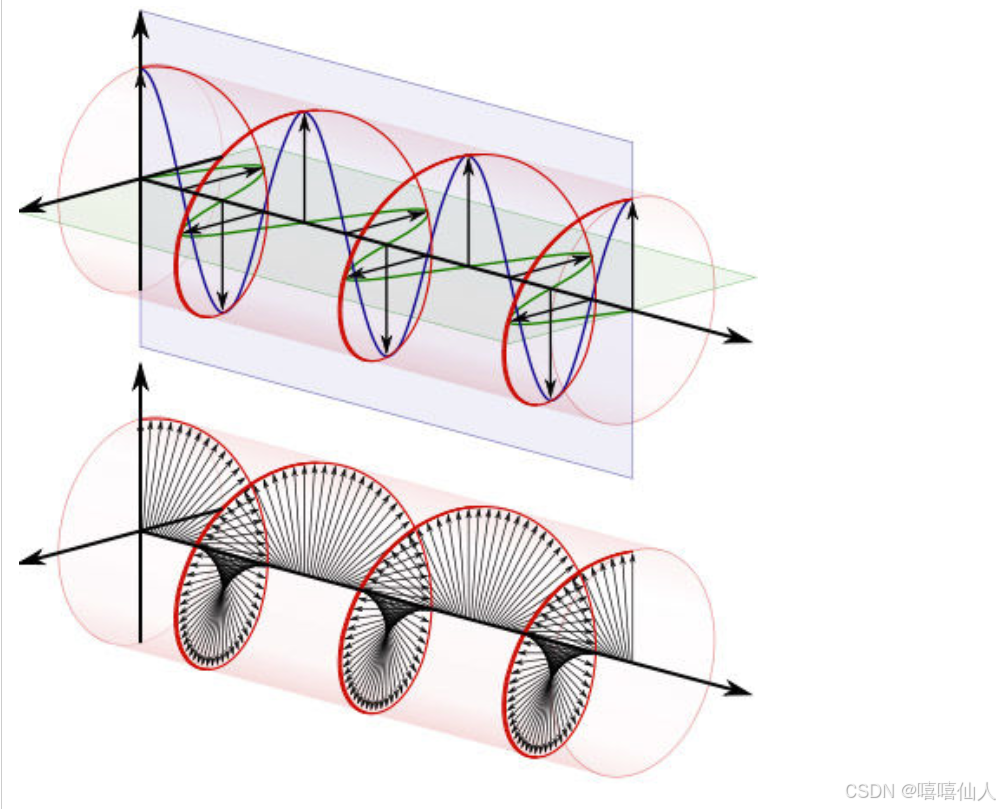
这个公式关键的作用,是将正弦波统一成了简单的指数形式。我们来看看图像上的涵义:

变成了一个螺旋线。是不是和电磁场很像?
我们即可以让电场强度与复数磁场强度相加而不损失各自的信息,又满足了电场与磁场90度垂直的要求
欧拉公式所描绘的,是一个随着时间变化,在复平面上做圆周运动的点,随着时间的改变,在时间轴上就成了一条螺旋线。如果只看它的实数部分,也就是螺旋线在左侧的投影,就是一个最基础的余弦函数。而右侧的投影则是一个正弦函数。
除此之外,欧拉公式还有另外一种表现形式:
我们刚才讲过,e^(it)可以理解为一条逆时针旋转的螺旋线,那么e^(-it)则可以理解为一条顺时针旋转的螺旋线。而 cos (t)则是这两条旋转方向不同的螺旋线叠加的一半,因为这两条螺旋线的虚数部分相互抵消掉了!
举个例子的话,就是极化方向不同的两束光波,磁场抵消,电场加倍。