Bootstrap

二叉排序树详解并通过Java代码实现

目录

什么是二叉排序树？

二叉排序树又叫二叉查找树、二叉搜索树、有序二叉树，再进行数据查找操作时，可以达到 O ( l o g n ) − O ( n ) O(logn) - O(n) O(logn)−O(n) 的时间复杂度。

给定一个二叉树，如果满足以下条件，那就是二叉排序树：

  1. 若它的左子树不空，则左子树上所有结点的值均小于它根结点的值。
  2. 若它的右子树不空，则右子树上所有结点的值均大于它根结点的值。
  3. 它的左、右子树都满足为⼆叉排序树。

二叉排序树的构建

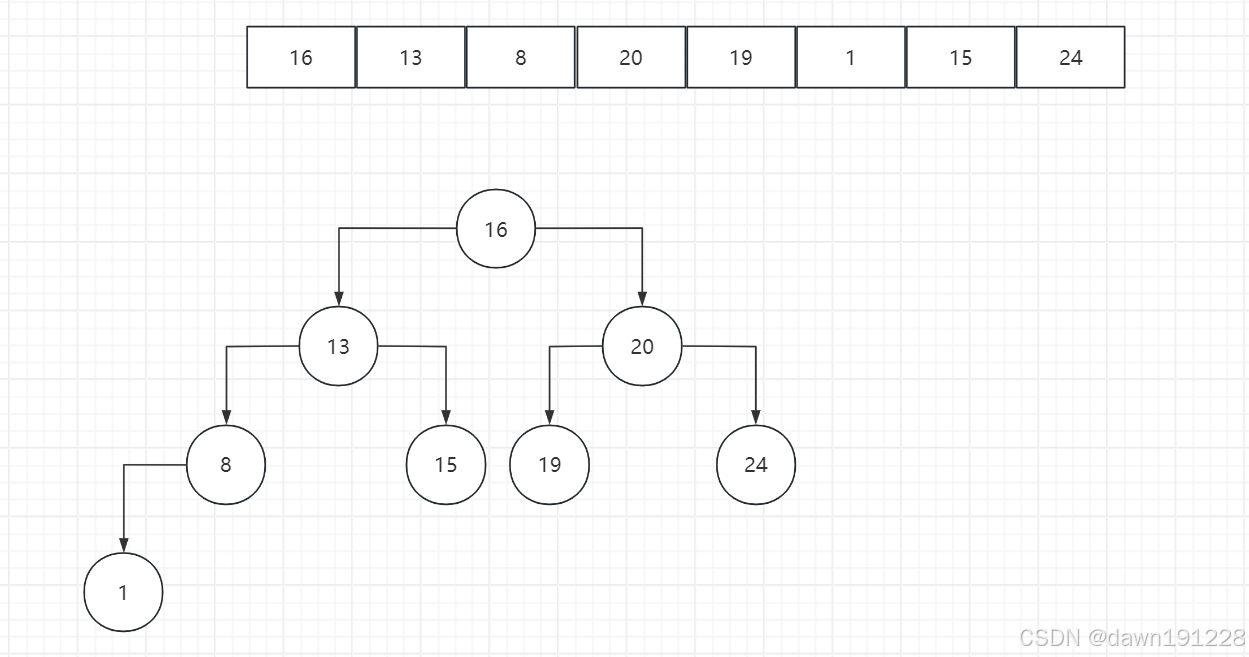
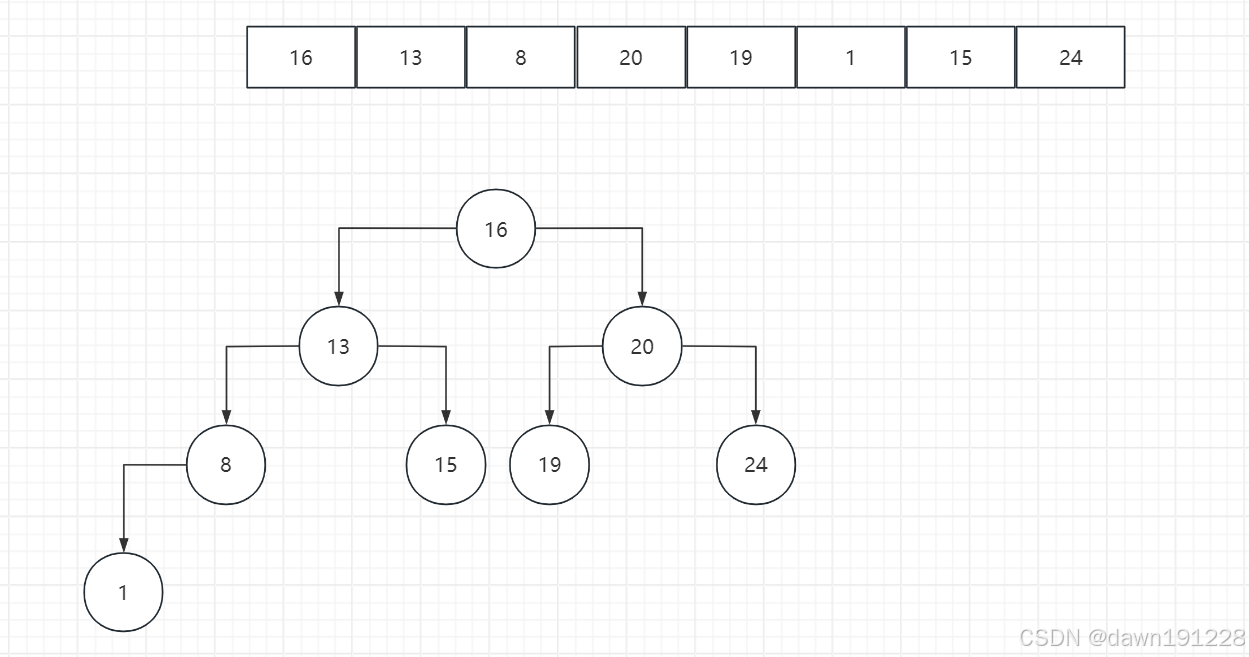
  • 二叉排序树从根节点开始构建，如果当前值比根节点小，则进入左子树，否则进入右子树。然后再递归的和左右孩子进行比较，直至将值添加到叶子节点。
    二叉树构建

  • 代码实现：首先定义一个二叉树的结构类，然后通过创建二叉树的管理类对二叉树进行操作，构造出二叉排序树。

public class TreeNode {
    private int value;
    private TreeNode left;
    private TreeNode right;

    public int getValue() {
        return value;
    }

    public void setValue(int value) {
        this.value = value;
    }

    public TreeNode getLeft() {
        return left;
    }

    public void setLeft(TreeNode left) {
        this.left = left;
    }

    public TreeNode getRight() {
        return right;
    }

    public void setRight(TreeNode right) {
        this.right = right;
    }

    public TreeNode(int value) {
        this.value = value;
    }

    @Override
    public String toString() {
        return "TreeNode{" +
                "value=" + value +
                ", left=" + left +
                ", right=" + right +
                '}';
    }
}

public class BinaryTree {
    public TreeNode root;
}

排序二叉树的增删查改

插入操作

  • 非递归方式实现：
public void insert(int value) {
    TreeNode node = new TreeNode(value);
    if(root == null) {//判断根节点是否为空
        root = node;
    } else { //定义一个游标遍历二叉树，在定义一个pre记录游标的前一个值
        TreeNode index = root;
        TreeNode pre = null;
        while (true) {
            pre = index;
            if (node.getValue() > index.getValue()) { //如果待插入值大于当前值，游标右移
                index = index.getRight();
                if (index == null) { //如果游标指空，说明到了叶子节点
                    pre.setRight(node);
                    break;
                }
            } else { //否则游标左移
                index = index.getLeft();
                if (index == null) { //如果游标指空，说明到了叶子节点
                    pre.setLeft(node);
                    break;
                }
            }
        }
    }
}
  • 递归方式实现：
public void insert(TreeNode node, int value) {
    TreeNode newNode = new TreeNode(value);
    if(root == null) {//判断根节点是否为空
        root = newNode;
    } else {
        if (node.getValue() > value) { //当前节点大于待插入值,向左递归
            if (node.getLeft() == null) {
                node.setLeft(newNode);
                return;
            }
            insert(node.getLeft(), value);
        } else { //向右递归
            if (node.getRight() == null) {
                node.setRight(newNode);
                return;
            }
            insert(node.getRight(), value);
        }
    }
}

查找操作

  • 非递归方式实现：
public TreeNode search(int value) {
    TreeNode index = root;
    while (index != null) {
        if (index.getValue() == value) { //找到了
            return index;
        } else if (index.getValue() < value) {
            index = index.getRight();
        } else {
            index = index.getLeft();
        }
    }
    return null;
}
  • 递归方式实现：
public TreeNode search(TreeNode node, int value) {
    if (node == null) {
        return null;
    } else {
        if (value == node.getValue()) {
            return node;
        } else if (value < node.getValue()) {
            return search(node.getLeft(), value);
        } else {
            return search(node.getRight(), value);
        }
    }
}

删除操作

//找到要删除节点的父节点
public TreeNode searchParent(TreeNode node, int value) {
    if (node == null) {
        return null;
    } else { //判断当前节点是否是目标节点的父节点
        if(node.getLeft() != null && node.getLeft().getValue() == value || node.getRight() != null && node.getRight().getValue() == value) {
            return node;
        } else if (value < node.getValue()) { //如果目标值小于当前节点值（并且node不是该值的父节点），说明目标节点的父节点在当前节点的左侧
            return searchParent(node.getLeft(), value);
        } else {
            return searchParent(node.getRight(), value);
        }
    }
}

public void delete(int value) {
    if (root == null) {
        System.out.println("空树!");
    } else {
        //1.找到目标节点
        TreeNode target = search(value);
        if (target == null) {
            System.out.println("没有目标节点!");
        } else {
            //2.找到目标节点的父节点
            TreeNode parent = searchParent(root, value);
            if (target.getLeft() == null && target.getRight() == null) { //2.1删除叶子节点
                if (parent == null) { //没有父节点
                    root = null;
                } else if (parent.getLeft() != null && parent.getLeft().getValue() == value) { //是左孩子
                    parent.setLeft(null);
                } else {
                    parent.setRight(null);
                }
            } else if (target.getLeft() != null && target.getRight() != null) { //2.2删除有两颗子树的节点
                //找到目标节点右子树的最小值
                TreeNode index = target.getRight();
                while (index.getLeft() != null) {
                    index = index.getLeft();
                }
                //index指向target的右子树的最小值
                int min = index.getValue();
                //删除target右子树的最小值，并覆盖给目标值
                delete(min);
                target.setValue(min);
            } else { //2.3删除只有一棵子树的节点
                if (parent == null) {
                    if (target.getLeft() != null) { //判断target有左子树还是右子树
                        root = target.getLeft();
                    } else {
                        root = target.getRight();
                    }
                } else { //有父节点
                    if (parent.getLeft() != null && parent.getLeft().getValue() == value) { //确定target是parent的左孩子还是右孩子
                        if (target.getLeft() != null) { //判断target自己有左子树还是右子树
                            parent.setLeft(target.getLeft());
                        } else {
                            parent.setLeft(target.getRight());
                        }
                    } else {
                        if (target.getLeft() != null) { //判断target自己有左子树还是右子树
                            parent.setRight(target.getLeft());
                        } else {
                            parent.setRight(target.getRight());
                        }
                    }
                }
            }
        }
    }
}

二叉排序树的遍历

样例

深度优先遍历

深度优先遍历（dfs）遍历方式输出结果
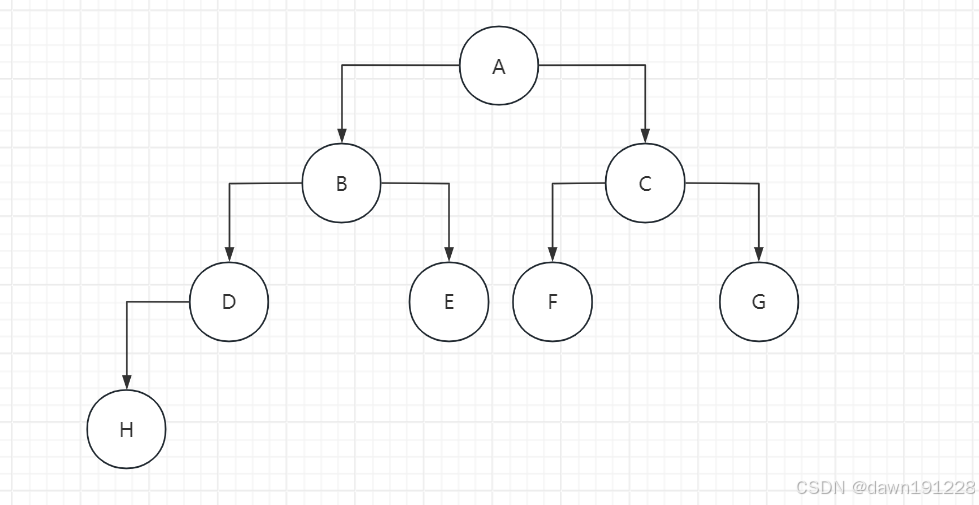
先序遍历先输出父节点，再输出左子树，再输出右子树 A − > B − > D − > H − > E − > C − > F − > G A->B->D->H->E->C->F->G A−>B−>D−>H−>E−>C−>F−>G
中序遍历先输出左子树，再输出父节点，再输出右子树 H − > D − > B − > E − > A − > F − > C − > G H->D->B->E->A->F->C->G H−>D−>B−>E−>A−>F−>C−>G
后序遍历先输出左子树，再输出右子树，再输出父节点 H − > D − > E − > B − > F − > G − > C − > A H->D->E->B->F->G->C->A H−>D−>E−>B−>F−>G−>C−>A
  • 由定义可知：二叉排序树的中序遍历构成一个有序序列。
public void beforeOrder(TreeNode node) {
    if (node == null) {
        return;
    } else {
        System.out.print(node.getValue() + " ");
        beforeOrder(node.getLeft());
        beforeOrder(node.getRight());
    }
}

public void middleOrder(TreeNode node) {
    if (node == null) {
        return;
    } else {
        middleOrder(node.getLeft());
        System.out.print(node.getValue() + " ");
        middleOrder(node.getRight());
    }
}

public void afterOrder(TreeNode node) {
    if (node == null) {
        return;
    } else {
        afterOrder(node.getLeft());
        afterOrder(node.getRight());
        System.out.print(node.getValue() + " ");
    }
}

广度优先遍历

广度优先遍历（bfs）输出结果
从上到下打印每个二叉树的节点，同一层的节点按照从左到右的顺序进行打印 A − > B − > C − > D − > E − > F − > G − > H A->B->C->D->E->F->G->H A−>B−>C−>D−>E−>F−>G−>H
public void levelOrder(TreeNode node) {
    Queue<TreeNode> queue = new LinkedList<TreeNode>(); //调用Java提供的队列类生成一个队列
    TreeNode index = null; //记录从队列中取出的节点
    if (node != null) {
        queue.add(node);
        while (!queue.isEmpty()) {
            index = queue.poll();
            System.out.print(index.getValue() + " ");
            if (index.getLeft() != null) {
                queue.add(index.getLeft());
            }
            if (index.getRight() != null) {
                queue.add(index.getRight());
            }
        }
    } else {
        System.out.println("树为空!");
    }
}

测试样例及代码

样例


public class Test {
    public static void main(String[] args) {
        BinaryTree tree = new BinaryTree();
        tree.insert(16);
        tree.insert(13);
        tree.insert(8);
        tree.insert(20);
        tree.insert(tree.root, 19);
        tree.insert(tree.root,1);
        tree.insert(tree.root,15);
        tree.insert(tree.root,24);

        tree.beforeOrder(tree.root);
        System.out.println();
        tree.middleOrder(tree.root);
        System.out.println();
        tree.afterOrder(tree.root);
        System.out.println();
        tree.levelOrder(tree.root);
        System.out.println();

        System.out.println("\n\n");

        TreeNode t1 = tree.search(20);
        System.out.println(t1);
        TreeNode t2 = tree.search(tree.root,13);
        System.out.println(t2);

        System.out.println("\n\n");

        tree.delete(13);
        System.out.println(tree);
    }
}
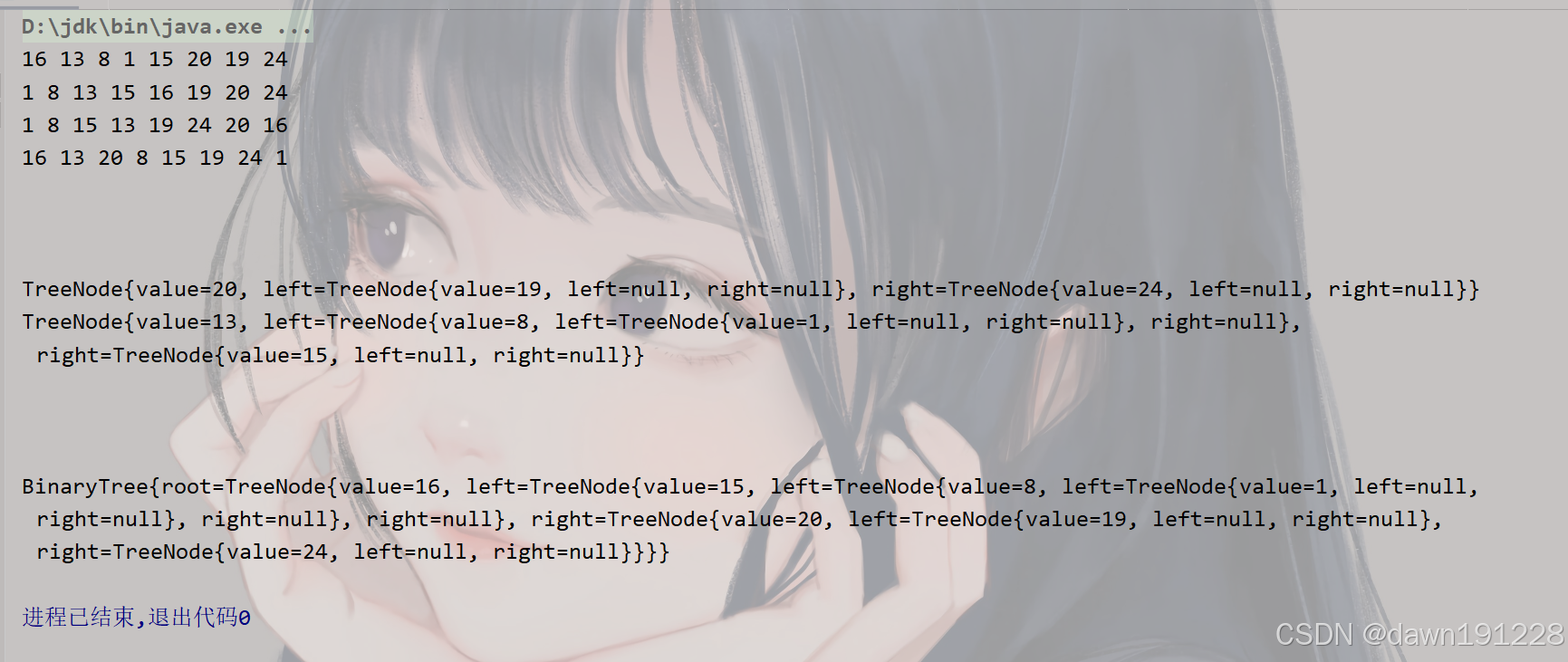
  • 测试结果如下：

测试结果

几种常见二叉树的区别

名称特性
完全二叉树数据从上到下，从左到右依次排列
满二叉树所有的叶子节点都在同一层，且最后一层的节点数为 2 n − 1 2^{n-1} 2n−1， n n n 表示层数
有序二叉树左边节点的值小于当前节点，右边节点的值大于当前节点
平衡二叉树平衡二叉树、B树、B+树、红黑树解析
红黑树平衡二叉树、B树、B+树、红黑树解析

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
机器学习算法-朴素贝叶斯算法
干巴巴的签到！
Pycharm-用鼠标滚轮放大缩小字体的大小
数据库--SQLServer--如何找到包含某列最大值的那一行
docker 安装es
Java初学-多态
【JVM】JVM基础
基于SpringBoot+微信小程序的医院预约叫号小程序
k8s上nginx无法正常转发socketIO
多表联合查询
;