论文笔记
资料
1.代码地址
https://github.com/qinenergy/cotta
2.论文地址
https://arxiv.org/abs/2203.13591
3.数据集地址
论文摘要的翻译
TTA的目的是在不使用任何源数据的情况下,将源预先训练的模型适应到目标域。现有的工作主要考虑目标域是静态的情况。然而,现实世界的机器感知系统运行在非静态和不断变化的环境中,其中目标域分布可能会随着时间的推移而变化。现有的方法大多基于自训练和熵正则化,可能会受到这些非平稳环境的影响。由于目标域中的分布随时间移动,伪标签变得不可靠。嘈杂的伪标签会进一步导致错误累积和灾难性的遗忘。为了解决这些问题,我们提出了一种连续测试时间适应方法(continual test-time adaptation,COTTA),该方法包括两个部分。首先,我们建议通过使用通常更准确的加权平均和增广平均预测来减少误差积累。另一方面,为了避免灾难性的遗忘,我们建议在每次迭代期间随机将一小部分神经元恢复到源预先训练的权重,以帮助长期保存源知识。该方法能够对网络中的所有参数进行长期自适应。CONTTA易于实施,并且可以很容易地整合到现成的预训练的模型中。我们在四个分类任务和一个连续测试时间自适应的分割任务上证明了我们的方法的有效性,我们在这方面的表现优于现有的方法。
1 介绍
TTA旨在通过在推理时从未标记的测试(目标)数据中学习来适配源预先训练的模型。由于源训练数据和目标测试数据之间的域分布差异,需要进行自适应以获得良好的性能。源数据通常被认为在推理时间内不可用,这使得它比无监督的域自适应更具挑战性但更现实。
现有的测试时间自适应工作通常通过使用伪标记法或熵正则化来更新模型参数来处理源域和固定目标域之间的分布差异
然而,当目标测试数据来自一个不断变化的环境时,它们可能是不稳定的。这有两个方面的原因:
首先,在不断变化的环境下,由于分布偏移,伪标签变得更噪声和错误校准。因此,早期预测错误更有可能导致误差累积。
其次,由于模型长时间地不断适应新的分布,来自源域的知识更难保存,导致灾难性的遗忘。
这里主要介绍online continual test-time adaptation的实际问题。
如图1所示,目标是从现成的源代码预先训练的模型开始,并不断地使其适应当前的测试数据。
为了有效地使预先训练源模型适应不断变化的测试数据,我们提出了一种连续测试时间自适应方法(COTTA),解决了现有方法的两个主要局限性。该方法的第一个组成部分旨在减少误差累积。我们建议在自训练框架下通过两种不同的方法来提高伪标签的质量。一方面,由于教师平均预测往往比标准模型[55]具有更高的质量,我们使用加权平均教师模型来提供更准确的预测。另一方面,对于领域差距较大的测试数据,我们使用了增广平均预测来进一步提高伪标签的质量。提出的方法的第二个组成部分旨在帮助保存源知识和避免遗忘。我们建议随机地将网络中的一小部分神经元恢复到预先训练的源模型。通过减少错误积累和保存知识,CONTTA能够在不断变化的环境中进行长期适应,并使训练网络的所有参数成为可能。相比之下,以前的方法只能训练BN的参数。
2论文的创新点
- 提出了一种连续的测试时间自适应方法COTTA,该方法能够有效地使现成的源预训练模型适应不断变化的目标数据。
- 具体地说,通过使用更准确的加权平均和增广平均伪标签来减少误差累积。
- 通过显式地保存来自源模型的知识来缓解长期遗忘效应。
- 该方法显著提高了分类基准和分割基准的continual test-time adaptation的性能。
3 Continual Test-Time Domain Adaptation方法的概述
3.1 问题定义
给定具有对源数据
(
X
S
,
Y
S
)
(\mathcal{X^S},\mathcal{Y^S})
(XS,YS)训练的参数
θ
θ
θ的现有预训练模型
f
θ
0
(
x
)
f_{θ_0}(x)
fθ0(x),在不访问任何源数据的情况下以在线方式不断变化的目标域。顺序地提供未标记的目标域数据
X
T
\mathcal{X^T}
XT,并且该模型只能访问当前时间步长的数据。在时间步长
t
t
t处,目标数据
X
t
T
X^T_t
XtT被提供作为输入,并且模型
f
θ
t
f_{θ_t}
fθt需要做出预测
f
θ
t
(
X
t
T
)
f_{θ_t}(X^T_t)
fθt(XtT),并相应地适应未来输入
θ
t
→
θ
t
+
1
θ_t→θ_{t+1}
θt→θt+1。
X
t
T
X^T_t
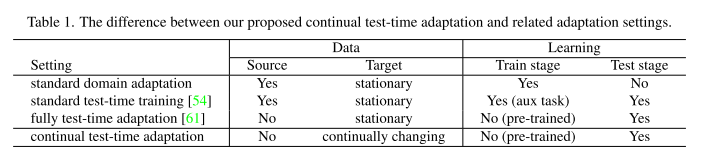
XtT的数据分布不断变化。根据在线预测对该模型进行了评估。这种设置在很大程度上是由于机器感知应用在不断变化的环境中的需求。我们在表1中列出了我们的在线连续测试时间适应设置与现有适应设置之间的主要区别。与以前专注于固定目标域的设置相比,我们考虑的是对不断变化的目标环境的长期适应
3.2 方法
提出了一种用于在线连续测试时间自适应设置的自适应方法。该方法采用现成的源预训练模型,并在线自适应不断变化的目标数据。基于错误累积是自训练框架中的关键瓶颈之一这一事实,我们提出使用加权和增强平均伪标签来减少错误累积。此外,为了帮助减少连续适应中的遗忘,我们建议显式保留来自源模型的信息。图2显示了所建议方法的概述。
3.2.1 Source Model
现有的测试时间自适应工作往往需要在源模型的训练过程中进行特殊处理,以提高领域泛化能力,促进自适应。本方法不需要修改体系结构或额外的源训练过程。因此,任何现有的预先训练的模型都可以使用,而不需要对源进行重新培训。
3.2.2 Weight-Averaged Pseudo-Labels
在给定目标数据
x
t
T
x^T_t
xtT和模型
f
θ
t
f_{θ_t}
fθt的情况下,自训练框架下的共同测试时间目标是最小化预测
y
^
t
T
=
f
θ
t
(
x
t
T
)
a
\hat{y}_{t}^{T} = f_{\theta_{t}}(x_{t}^{T}) \mathrm{a}
y^tT=fθt(xtT)a和伪标签之间的交叉熵一致性。例如,直接使用模型预测本身作为伪标签导致TENT[61]的训练目标(即熵最小化)。虽然这对固定的目标域有效,但由于分布偏移,对于不断变化的目标数据,伪标签的质量可能会显著下降。
由于观察到训练步骤中的加权平均模型通常比最终模型提供更准确的模型,我们使用加权平均教师模型
f
θ
′
f_{\theta^{\prime}}
fθ′来生成伪标签。在时间步长
t
=
0
t=0
t=0时,教师网络被初始化为与源预训练网络相同。在时间处于
t
t
t时,首先由教师
y
′
^
t
T
=
f
θ
t
′
(
x
t
T
)
.
\hat{y^{\prime}}_{t}^{T}=f_{\theta_{t}^{\prime}}(x_{t}^{T}).
y′^tT=fθt′(xtT).生成伪标签。
然后通过学生和教师预测之间的交叉点损失来更新学生
f
θ
t
f_{θ_t}
fθt
L
θ
t
(
x
t
T
)
=
−
∑
c
y
′
^
t
c
T
log
y
^
t
c
T
,
(
1
)
\mathcal{L}_{\theta_{t}}(x_{t}^{T})=-\sum_{c}\hat{y'}_{tc}^{T}\log\hat{y}_{tc}^{T},\quad(1)
Lθt(xtT)=−c∑y′^tcTlogy^tcT,(1)
在使用公式1更新学生模型
θ
t
→
θ
t
+
1
θ_t→θ_{t+1}
θt→θt+1之后,我们使用学生权重通过指数移动平均来更新教师模型的权重
θ
t
+
1
′
=
α
θ
t
′
+
(
1
−
α
)
θ
t
+
1
,
(
2
)
\theta'_{t+1}=\alpha\theta'_t+(1-\alpha)\theta_{t+1},\quad(2)
θt+1′=αθt′+(1−α)θt+1,(2)
其中,α是一个平滑因子。我们对输入数据
x
t
T
x^T_t
xtT的最终预测是
y
′
^
t
T
\hat{y^{\prime}}_{t}^{T}
y′^tT中具有最高概率的类。
重量平均一致性的好处有两个。一方面,通过使用通常更准确的加权平均预测作为伪标签目标,我们的模型在连续自适应过程中遭受的误差累积较少。
另一方面,平均教师预测
y
′
^
t
T
\hat{y^{\prime}}_{t}^{T}
y′^tT编码了过去迭代中来自模型的信息,因此在长期的连续适应中不太可能遭受灾难性遗忘,并提高了对新的未知领域的泛化能力。
3.2.3 Augmentation-Averaged Pseudo-Labels
训练时间内的数据扩充已被广泛应用于提高模型的性能。对于不同的数据集,通常手动设计或搜索不同的扩充策略。虽然测试时间扩充也已被证明能够提高稳健性,但扩充策略通常是针对特定数据集确定和固定的,而不考虑推理时间期间的分布变化。在不断变化的环境下,测试分发可能会发生巨大变化,这可能会使增强策略无效。在这里,我们考虑了测试时间域的分布差异,并用预测置信度来逼近域差异。仅当域差异较大时才应用增强,以减少误差累积。
y
′
~
t
T
=
1
N
∑
i
=
0
N
−
1
f
θ
t
′
(
arg
i
(
x
t
T
)
)
,
(3)
y
′
t
T
=
{
y
′
^
t
T
,
if conf
(
f
θ
0
(
x
t
T
)
)
≥
p
t
h
y
′
~
t
T
,
otherwise
,
(4)
\begin{aligned}\tilde{y'}_{t}^{T}&=\frac{1}{N}\sum_{i=0}^{N-1}f_{\theta_{t}^{'}}(\arg_{i}(x_{t}^{T})),&\text{(3)}\\{y'}_{t}^{T}&=\begin{cases}\hat{y'}_{t}^{T},&\text{if conf}(f_{\theta_{0}}(x_{t}^{T}))\geq p_{th}\\\tilde{y'}_{t}^{T},&\text{otherwise},\end{cases}&\text{(4)}\end{aligned}
y′~tTy′tT=N1i=0∑N−1fθt′(argi(xtT)),={y′^tT,y′~tT,if conf(fθ0(xtT))≥pthotherwise,(3)(4)
其中
y
′
~
t
T
\widetilde{y^{\prime}}_{t}^{T}
y′
tT是来自教师模型的增广平均预测,
y
′
^
t
T
\hat{y^{\prime}}_{t}^{T}
y′^tT是来自教师模型的直接预测,
c
o
n
f
(
f
θ
0
(
X
t
T
)
)
conf(f_{θ_0}(X_t^T))
conf(fθ0(XtT)) 是源预训练模型对当前输入
x
t
T
x^T_t
xtT的预测置信度,以及
P
t
h
P_{th}
Pth是置信度阈值。通过使用公式4中的预训练模型
f
θ
0
来
f_{θ_0}来
fθ0来计算对当前输入Xtt的预测置信度,我们试图逼近源和当前域之间的域差异。我们假设较低的置信度表示较大的域间隙,而相对较高的置信度表示较小的域间隙。因此,当置信度高且大于阈值时,我们直接使用
y
′
^
t
T
\hat{y^{\prime}}_{t}^{T}
y′^tT作为我们的伪标签,而不使用任何增广。当置信度较低时,我们采用额外的N个随机增强来进一步提高伪标签的质量。过滤是至关重要的,过滤是至关重要的,因为我们观察到随机增强,因为我们观察到,在具有小域间隙的自信样本上的随机增加有时会降低模型的性能。我们在补充材料中对这一观察结果进行了详细讨论。总而言之,我们使用置信度来逼近域差异,并确定何时应用扩展。学生通过改进的伪标签进行更新:
3.2.4 Stochastic Restoration
虽然更准确的伪标签可以减少错误积累,但长期自我训练的持续适应不可避免地会引入错误并导致遗忘。如果我们在数据序列中遇到强烈的域移,这个问题可能特别相关,因为强烈的分布移位会导致错误校准甚至错误的预测。在这种情况下,自我训练可能只会强化错误的预测。更糟糕的是,在遇到硬性例子后,即使新数据没有严重漂移,模型也可能因为不断的适应而无法恢复。为了进一步解决灾难性遗忘问题,我们提出了一种随机恢复方法,该方法显式地恢复源预先训练模型中的知识。考虑基于时间步
t
t
t处的公式1的梯度更新之后的学生模型
f
θ
f_θ
fθ内的卷积层:
x
l
+
1
=
W
t
+
1
∗
x
l
,
(
6
)
x_{l+1}=W_{t+1}*x_{l},\quad(6)
xl+1=Wt+1∗xl,(6)其中,∗表示卷积运算,
x
l
和
x
l
+
1
x_l和x_{l + 1}
xl和xl+1表示到该层的输入和输出,
W
t
+
1
W_{t + 1}
Wt+1表示可训练的卷积滤波器。建议的随机恢复方法还通过以下方式更新权重
W
W
W:
M
∼
Bernoulli
(
p
)
,
(
7
)
W
t
+
1
=
M
⊙
W
0
+
(
1
−
M
)
⊙
W
t
+
1
,
(
8
)
\begin{aligned}M&\sim\text{Bernoulli}(p),\quad&(7)\\W_{t+1}&=M\odot W_0+(1-M)\odot W_{t+1},\quad&(8)\end{aligned}
MWt+1∼Bernoulli(p),=M⊙W0+(1−M)⊙Wt+1,(7)(8)其中同
⊙
\odot
⊙表示逐个元素的乘法。
p
p
p是一个小的恢复概率,
M
是与
W
t
+
1
M是与W_{t+1}
M是与Wt+1形状相同的掩模张量。随机恢复也可以看作是丢弃的一种特殊形式。通过随机地将可训练权值中的少量张量元素恢复到初始权值,网络避免了距离初始源模型太远的漂移,从而避免了灾难性遗忘。此外,通过保存来自源模型的信息,我们能够训练所有可训练的参数,而不会遭受模型崩溃的痛苦。这为自适应带来了更多的容量,并且与仅训练用于测试时间自适应的BN参数的熵最小化方法如算法1所示,将改进的伪标记法与随机恢复相结合,得到了在线连续测试时间自适应(COTTA)方法。
4 论文实验
五个连续测试时间自适应基准任务:CIFAR10-to-CIFAR10C(标准和渐进式)、CIFAR100-to-CIFAR100C、ImageNet-to-ImageNet-C以及用于语义分割的Cityscapses-to-ACDC上对我们的方法进行了评估。
4.1 Experiments on CIFAR10-to-CIFAR10C
我们首先评估了所提出的模型在CIFAR10到CIFAR10C任务上的有效性。我们将我们的方法与纯源代码基线和四种流行的方法进行了比较。
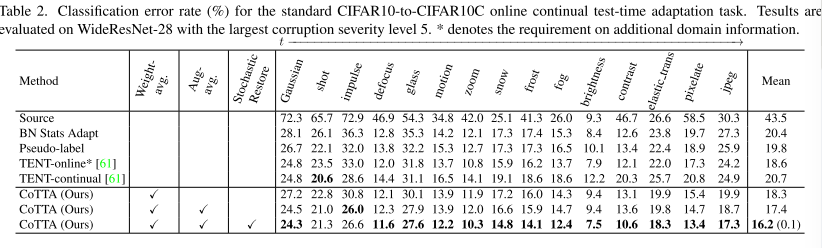
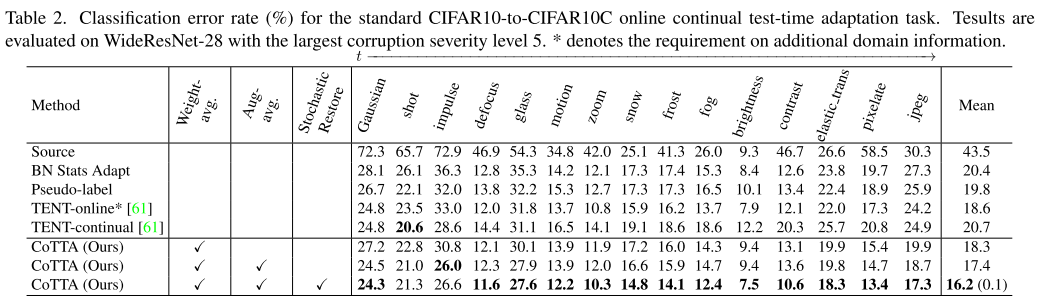
如表2所示,直接使用没有自适应的预训练模型产生了43.5%的高平均错误率,表明自适应是必要的。BN统计自适应方法保持网络权重,并使用来自当前迭代的输入数据的批量归一化统计用于预测。该方法简单且完全在线,在仅限源代码的基线上显著提高了性能。使用硬伪标签来更新BN可训练参数可以将错误率降低到19.8%。如果帐篷在线方法能够访问附加域信息,并在遇到新域时将其自身重置为初始的预训练模型,则性能可以进一步提高到18.6%。然而,这样的信息在实际应用中通常是不可用的。如果不能访问这些附加信息,帐篷连续方法不会比BNStats Adapt方法产生任何改进。值得一提的是,在适应的早期阶段,帐篷持续的表现优于国阵统计适应。然而,在观察到三种类型的腐败后,该模型很快就恶化了。这表明,由于误差累积,基于帐篷的方法在长期持续适应下可能不稳定。通过使用加权平均一致性,我们提出的方法可以持续地优于上述所有方法。误码率显著降低到16.2%。此外,由于我们的随机恢复方法,它在长期内不会受到性能下降的影响。
这一部分的消融实验
表2的下部分
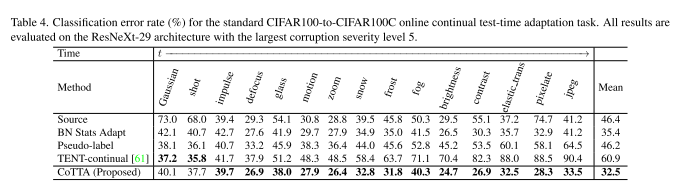
4.2 Experiments on CIFAR100-to-CIFAR100C
为了进一步证明所提方法的有效性,我们在难度更大的CIFAR100to-CIFAR100C任务上进行了评估。表4总结了实验结果。
4.3 Experiments on ImageNet-to-ImageNet-C
为了对所提出的方法进行更全面的评估,在严重性级别为5的10个不同的腐败类型序列上进行了ImageNet到ImageNet-C的实验。如表6所示,CONTA能够持续地优于帐篷和其他竞争方法。±之后的数字是10种不同损坏类型序列的标准偏差。
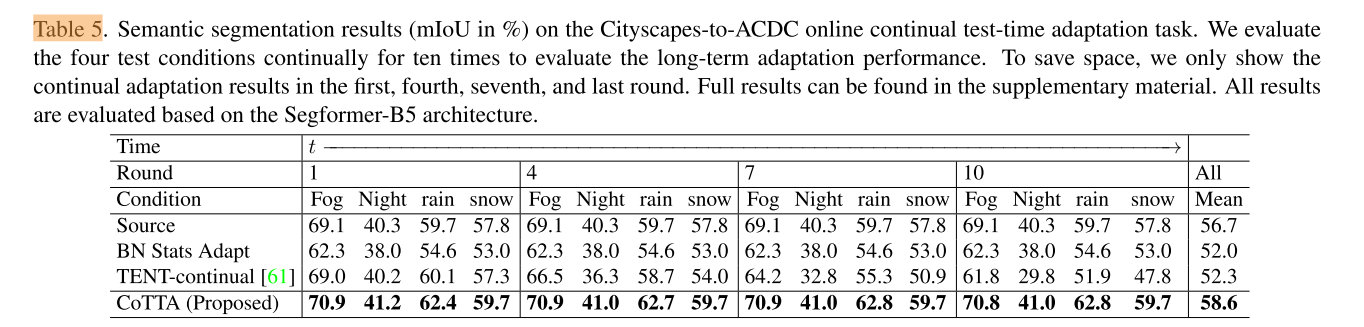
4.4 Experiments on Cityscapes-to-ACDC
此外,我们还在更复杂的连续测试时间语义分割Cityscapesto-ACDC任务上对我们的方法进行了评估。实验结果如表5所示。实验结果表明,我们的方法对于语义分割任务也是有效的,并且对不同的体系结构选择具有较强的鲁棒性。我们提出的方法在基准的基础上产生了1.9%的绝对改进,并且达到了58.6%的MIU.值得一提的是,BN统计适应和帐篷在这项任务中表现不佳,随着时间的推移,性能会显著下降。这在一定程度上是因为两者都是专门为具有批归一化层的网络设计的,而Segformer中只有一个批归一化层,而transform模型中的大多数归一化层都基于LayerNorm。然而,我们的方法不依赖于特定的层,并且仍然可以在非常不同的体系结构上有效地完成这项更复杂的任务。改进的性能在经过相对较长的时间不断调整后也基本保持不变。
5 总结
在这项工作中,关注的是在非静态环境中的连续测试时间适应,其中目标域分布可以随着时间的推移而不断变化。为了解决这种方法中的误差累积和灾难性遗忘问题,我们提出了一种新的方法COTTA,该方法包括两部分。==首先,我们通过使用加权平均和增广平均预测来减少误差积累,这两种预测往往更准确。==其次,为了保存来自源模型的知识,我们随机地将一小部分权重恢复到源预先训练的权重。所提出的方法可以结合到现成的预训练模型中,而不需要对源数据的任何访问。在4个分类和1个分割任务上验证了COTTA的有效性。