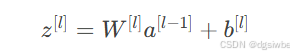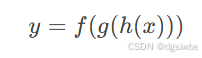BP算法的核心思想是通过计算损失函数对网络参数的梯度,然后使用梯度下降法来更新网络参数,从而最小化损失函数。
误差反向传播算法(BP)的基本步骤:
-
前向传播:正向计算得到预测值。
-
计算损失:通过损失函数计算预测值和真实值的差距。
-
梯度计算:反向传播的核心是计算损失函数对每个权重和偏置的梯度。
-
更新参数:一旦得到每层梯度,就可以使用梯度下降算法来更新每层的权重和偏置,使得损失逐渐减小。
-
迭代训练:将前向传播、梯度计算、参数更新的步骤重复多次,直到损失函数收敛或达到预定的停止条件。
前向传播
英文(Foward propagathon),表示将输入的数据逐级向前的每个神经元运算传输,直到到达输出层。
前向传播的目的是计算网络的预测值,以便后续计算损失函数并进行反向传播。
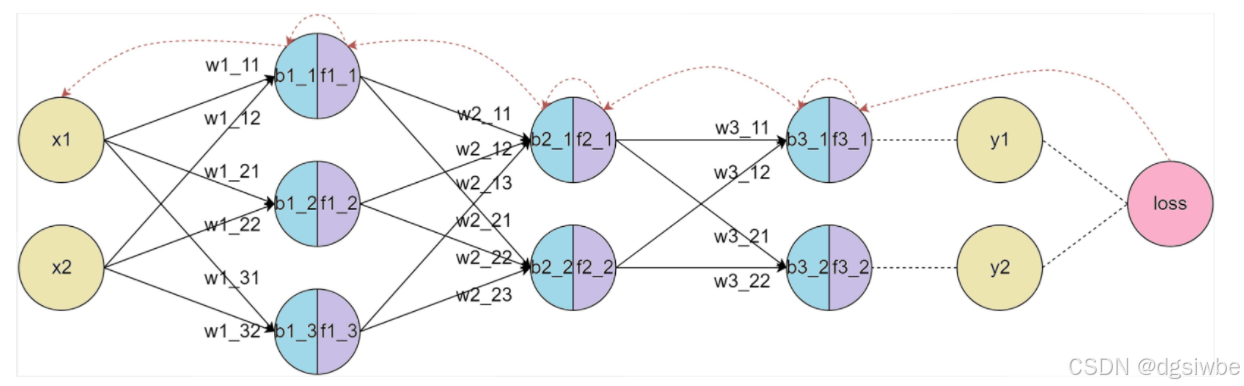
以下是一个三层神经网络实例,包含输入层(x1,x2,x3,b),隐藏层,输出层
链接输入和隐藏层的就是我们熟知的权重(w),在隐藏层中会完成两个动作
1.加权求和再求平均值,用于预测或计算损失。
2.再就是使用激活函数,将原本的线性公式,运算转为非线性。激活函数的使用视数据的情况而定
通常有sigmoid,Tanh,ReLu,softmax等激活函数。
x1,x2,x3,x4每个特征向量分别对隐藏层的n个神经元做线性运算,
再经过激活函数激活后得到最终预测值。
第一层的输出值等于第二层的输入值,依次经过运算。
代码逻辑:
def test():
# 前向传播
i = torch.tensor([0.05,0.1])
model1 = torch.nn.Linear(2,2)
model1.weight.data = torch.tensor([
[0.15,0.20],[0.25,0.30]
])
model1.bias.data = torch.tensor([0.35,0.35])
l1_l2 = model1(i)
h1_h2 = torch.nn.Sigmoid(l1_l2)
model2 = torch.nn.Linear(2,2)
model2.weight.data = torch.tensor([
[0.40,0.45],[0.50,0.55]
])
model2.bias.data = torch.tensor([0.60,0.60])
l3_l4 = model2(h1_h2)
o1_02 = torch.nn.Sigmoid(l3_l4)反向传播
通过计算损失函数相对于每个参数的梯度来调整权重,使模型在训练数据上的表现逐渐优化。反向传播结合了链式求导法则和梯度下降算法,是神经网络模型训练过程中更新参数的关键步骤。
前向传播的作用就是为了得到预测值,然后来为反向传播做准备。
反向传播是为了得到更好的w,也就是我们的权重。
链式法则
在深度学习中,链式法则是反向传播算法的基础,这样就可以通过分层的计算求得损失函数相对于每个参数的梯度。
复合函数的复杂性:
-
神经网络的输出是输入数据经过多层线性变换和非线性激活函数后的结果。每一层的输出都是下一层的输入,形成了一个复合函数。
-
例如,假设有一个三层神经网络,输出 yy 可以表示为:
-
其中,f、g、h 分别是不同层的激活函数。
链式求导法通过将复合函数的导数分解为各个简单函数的导数的乘积,简化了求导过程。
也就是求得我们每一层的导函数,以便于做梯度更新,找到最小损失。
反向传播中的数学运算。
实在看不懂数学公式。。。
直接上API。
import torch
#第一步,创建一个神经网络类,继承官方的nn.module
class mybet(torch.nn.Module):
#定义网络结构
def __init__(self,input_size,output_size):
#初始化父类:语法要求调用super方法生成父类的功能让子类继承父类的功能
super(mybet,self).__init__()
#定义网格结构
self.hide1 = torch.nn.Sequential(torch.nn.Linear(input_size,3),torch.nn.Sigmoid())
self.hide2 = torch.nn.Sequential(torch.nn.Linear(3,2),torch.nn.Sigmoid())
self.out = torch.nn.Sequential(torch.nn.Linear(2,output_size),torch.nn.Sigmoid())
def forward(self,input):
input.shape[1]
x = self.hide1(input)
x = self.hide2(x)
pred = self.out(x)
return pred
def train():
#数据集读取(这里自己编)
input = torch.tensor([[0.5, 0.1],
[0.05, 0.180],
[0.05, 0.310]])
target = torch.tensor([[1, 2],
[0, 3],
[1, 123]], dtype=torch.float32)
#创建网格
net = mybet(2,2)
#定义损失函数
loos_func = torch.nn.MSELoss()
#定义优化器
optimizer = torch.optim.SGD(net.parameters(),lr=0.01)
#训练
for epoch in range(500):
#前向传播
y_pred = net(input)
#计算损失
loss = loos_func(y_pred,target)
#梯度清零
optimizer.zero_grad()
#反向传播(计算每一层w的偏导数(梯度值))
loss.backward()
print(net.hide1[0].weight)
break
if __name__ == '__main__':
train()完整的全连接。