目录
反向传播算法
反向传播算法(Backpropagation)是训练人工神经网络时使用的一个重要算法,它是通过计算梯度并优化神经网络的权重来最小化误差。反向传播算法的核心是基于链式法则的梯度下降优化方法,通过计算误差对每个权重的偏导数来更新网络中的参数。
反向传播算法基本步骤:
前向传播:将输入数据传递通过神经网络的各层,计算每一层的输出。
计算损失:根据输出和实际标签计算损失(通常使用均方误差或交叉熵等作为损失函数)。
反向传播:根据损失函数对每个参数(如权重、偏置)计算梯度。梯度的计算通过链式法则进行反向传播,直到达到输入层。
更新权重:使用梯度下降算法来更新每一层的权重和偏置,使得损失函数最小化。
链式推到:https://blog.csdn.net/dingyahui123/category_6945552.html?spm=1001.2014.3001.5482
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.keras.datasets import mnist
# 加载 MNIST 数据集
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
# 归一化数据并将其形状调整为 (N, 784),因为每张图片是 28x28 像素
train_images = train_images.reshape(-1, 28*28) / 255.0
test_images = test_images.reshape(-1, 28*28) / 255.0
# 转换标签为 one-hot 编码
train_labels = np.eye(10)[train_labels]
test_labels = np.eye(10)[test_labels]
# 定义激活函数
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# 定义激活函数的导数
def sigmoid_derivative(x):
return x * (1 - x)
# 网络架构参数
input_size = 28 * 28 # 输入层的大小
hidden_size = 128 # 隐藏层的大小
output_size = 10 # 输出层的大小
# 初始化权重和偏置
W1 = np.random.randn(input_size, hidden_size) # 输入层到隐藏层的权重
b1 = np.zeros((1, hidden_size)) # 隐藏层的偏置
W2 = np.random.randn(hidden_size, output_size) # 隐藏层到输出层的权重
b2 = np.zeros((1, output_size)) # 输出层的偏置
# 设置超参数
epochs = 20
learning_rate = 0.1
batch_size = 64
# 训练过程
for epoch in range(epochs):
for i in range(0, len(train_images), batch_size):
# 选择当前batch的数据
X_batch = train_images[i:i+batch_size]
y_batch = train_labels[i:i+batch_size]
# 前向传播
z1 = np.dot(X_batch, W1) + b1
a1 = sigmoid(z1)
z2 = np.dot(a1, W2) + b2
a2 = sigmoid(z2)
# 计算损失的梯度
output_error = a2 - y_batch # 损失函数的梯度
output_delta = output_error * sigmoid_derivative(a2)
hidden_error = output_delta.dot(W2.T)
hidden_delta = hidden_error * sigmoid_derivative(a1)
# 更新权重和偏置
W2 -= learning_rate * a1.T.dot(output_delta)
b2 -= learning_rate * np.sum(output_delta, axis=0, keepdims=True)
W1 -= learning_rate * X_batch.T.dot(hidden_delta)
b1 -= learning_rate * np.sum(hidden_delta, axis=0, keepdims=True)
# 每10轮输出一次损失
if epoch % 10 == 0:
loss = np.mean(np.square(a2 - y_batch))
print(f"Epoch {epoch}, Loss: {loss}")
# 测试模型
z1 = np.dot(test_images, W1) + b1
a1 = sigmoid(z1)
z2 = np.dot(a1, W2) + b2
a2 = sigmoid(z2)
# 计算准确率
predictions = np.argmax(a2, axis=1)
true_labels = np.argmax(test_labels, axis=1)
accuracy = np.mean(predictions == true_labels)
print(f"Test Accuracy: {accuracy * 100:.2f}%")
# 可视化前5个测试图像及其预测结果
for i in range(5):
plt.imshow(test_images[i].reshape(28, 28), cmap='gray')
plt.title(f"Predicted: {predictions[i]}, Actual: {true_labels[i]}")
plt.show()
反向中的参数变化
import numpy as np
import matplotlib.pyplot as plt
import imageio
# 激活函数和其导数
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(x):
return x * (1 - x)
# 生成一些示例数据
np.random.seed(0)
X = np.array([[0, 0],
[0, 1],
[1, 0],
[1, 1]])
y = np.array([[0], [1], [1], [0]]) # XOR 问题
# 初始化参数
input_layer_neurons = 2
hidden_layer_neurons = 2
output_neurons = 1
learning_rate = 0.5
epochs = 10000
# 初始化权重
weights_input_hidden = np.random.uniform(size=(input_layer_neurons, hidden_layer_neurons))
weights_hidden_output = np.random.uniform(size=(hidden_layer_neurons, output_neurons))
# 存储权重和图像
weights_history = []
losses = []
images = []
# 训练过程
for epoch in range(epochs):
# 前向传播
hidden_layer_input = np.dot(X, weights_input_hidden)
hidden_layer_output = sigmoid(hidden_layer_input)
output_layer_input = np.dot(hidden_layer_output, weights_hidden_output)
predicted_output = sigmoid(output_layer_input)
loss = np.mean((y - predicted_output) ** 2)
losses.append(loss)
# 反向传播
error = y - predicted_output
d_predicted_output = error * sigmoid_derivative(predicted_output)
error_hidden_layer = d_predicted_output.dot(weights_hidden_output.T)
d_hidden_layer = error_hidden_layer * sigmoid_derivative(hidden_layer_output)
# 更新权重
weights_hidden_output += hidden_layer_output.T.dot(d_predicted_output) * learning_rate
weights_input_hidden += X.T.dot(d_hidden_layer) * learning_rate
# 保存权重
weights_history.append((weights_input_hidden.copy(), weights_hidden_output.copy()))
# 每1000次迭代保存一次图像
if epoch % 1000 == 0:
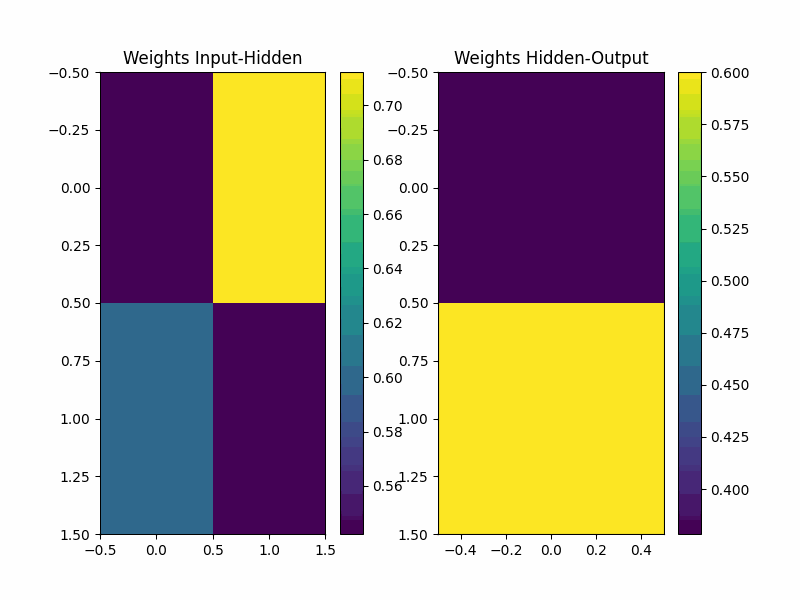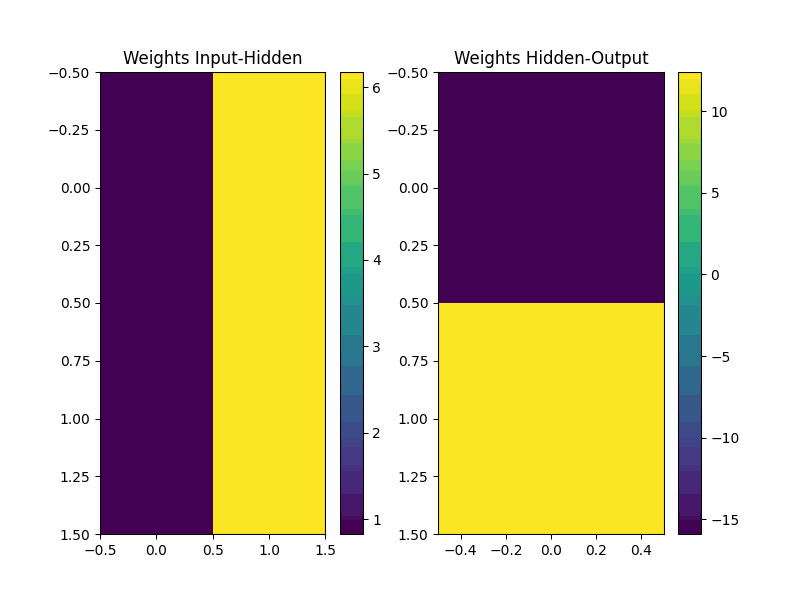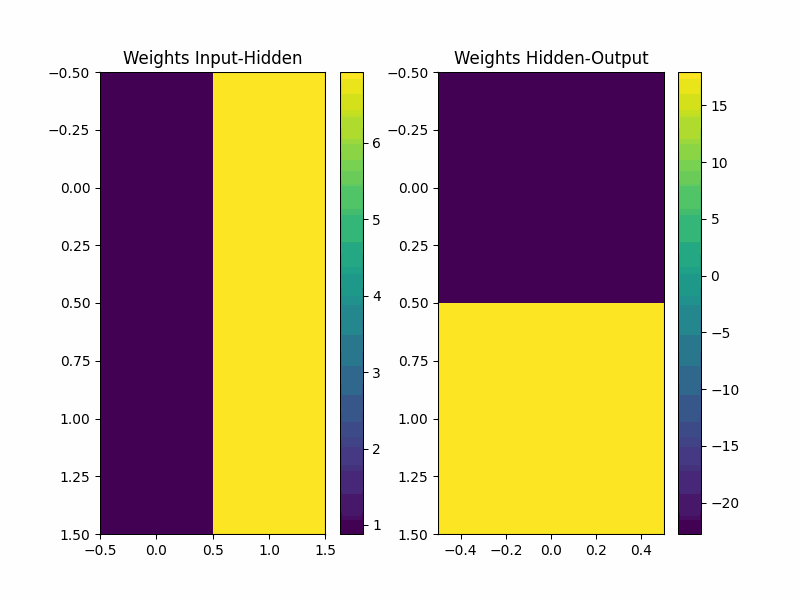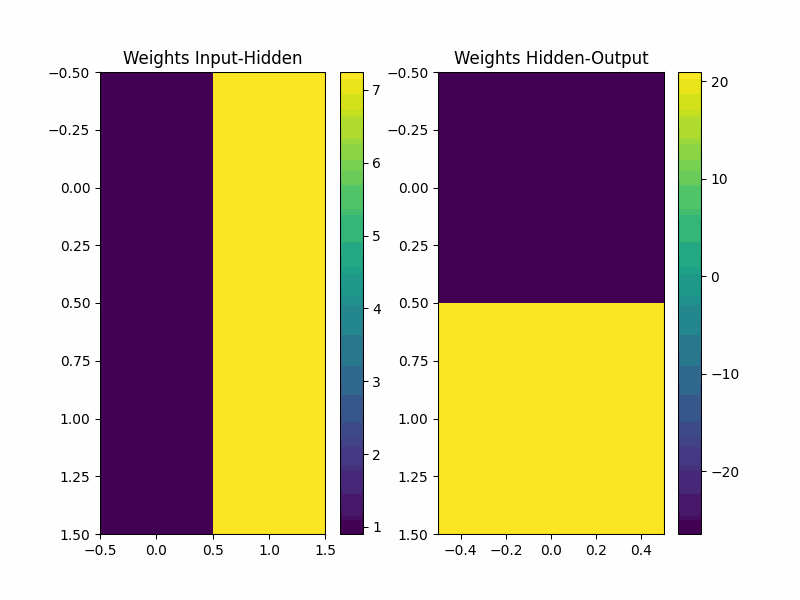
plt.figure(figsize=(8, 6))
plt.subplot(1, 2, 1)
plt.title('Weights Input-Hidden')
plt.imshow(weights_input_hidden, cmap='viridis', aspect='auto')
plt.colorbar()
plt.subplot(1, 2, 2)
plt.title('Weights Hidden-Output')
plt.imshow(weights_hidden_output, cmap='viridis', aspect='auto')
plt.colorbar()
# 保存图像
plt.savefig(f'weights_epoch_{epoch}.png')
plt.close()
if epoch % 1000 == 0:
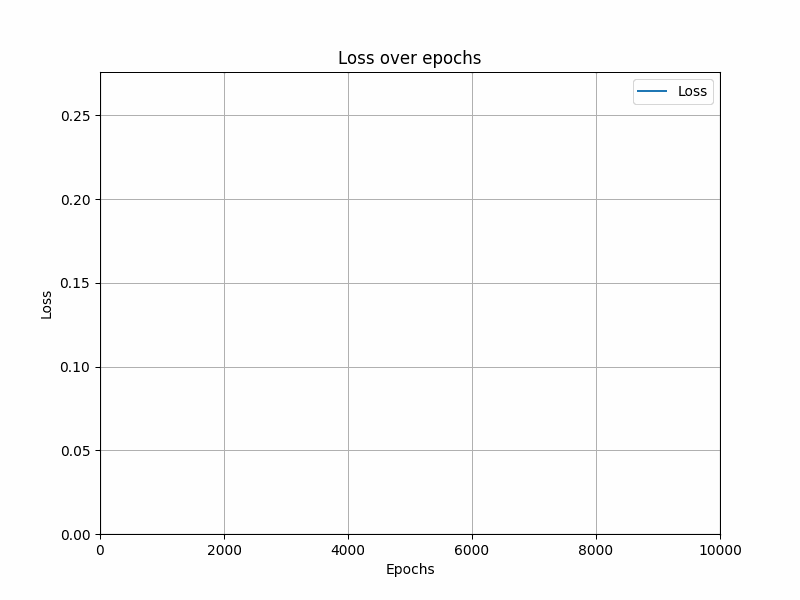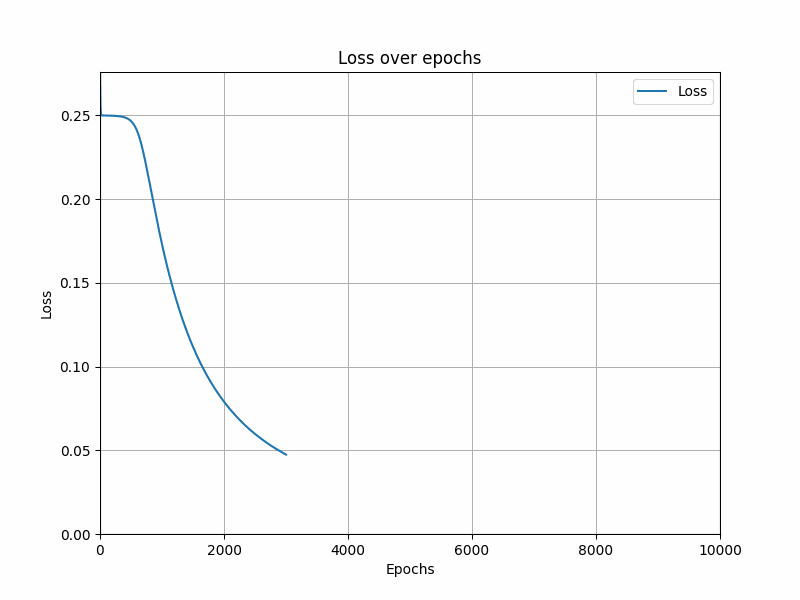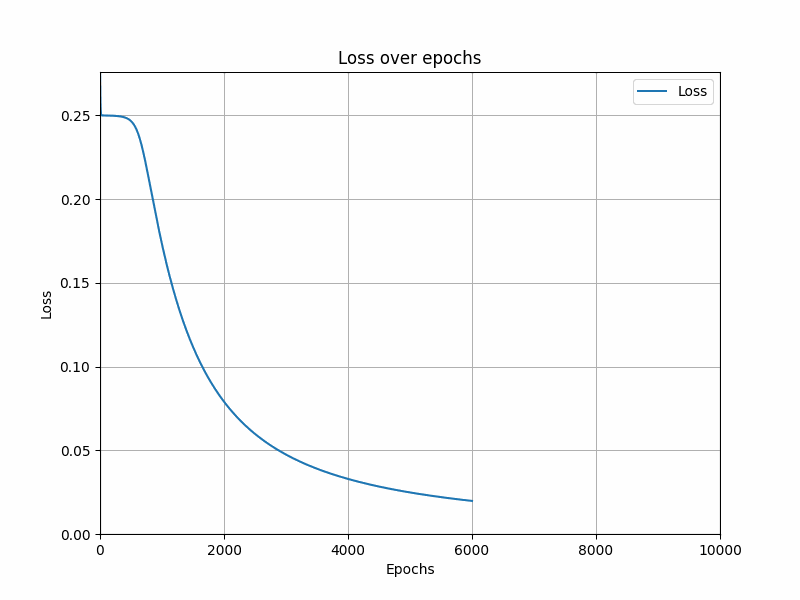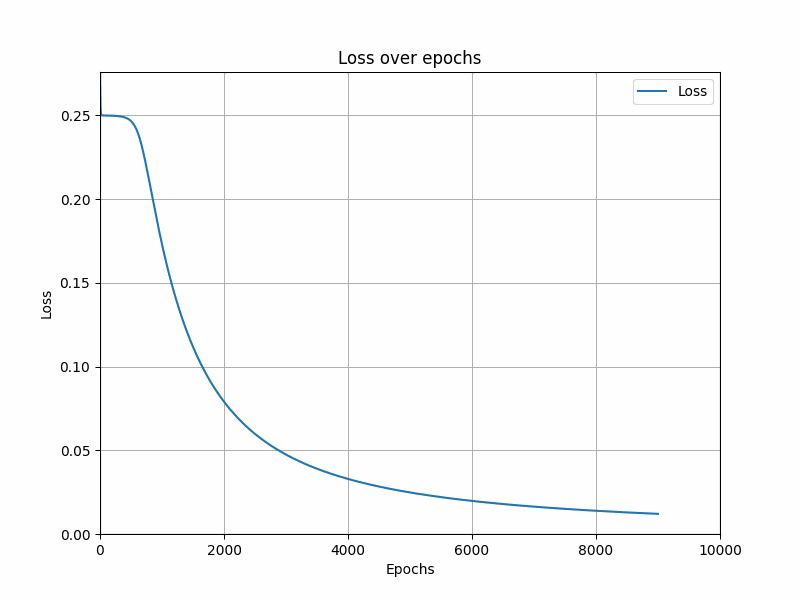
plt.figure(figsize=(8, 6))
plt.plot(losses, label='Loss')
plt.title('Loss over epochs')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.xlim(0, epochs)
plt.ylim(0, np.max(losses))
plt.grid()
plt.legend()
# 保存图像
plt.savefig(f'loss_epoch_{epoch}.png')
plt.close()
# 创建 GIF
with imageio.get_writer('weights_update.gif', mode='I', duration=0.5) as writer:
for epoch in range(0, epochs, 1000):
image = imageio.imread(f'weights_epoch_{epoch}.png')
writer.append_data(image)
# 创建 GIF
with imageio.get_writer('training_loss.gif', mode='I', duration=0.5) as writer:
for epoch in range(0, epochs, 1000):
image = imageio.imread(f'loss_epoch_{epoch}.png')
writer.append_data(image)
# 清理生成的图像文件
import os
for epoch in range(0, epochs, 1000):
os.remove(f'weights_epoch_{epoch}.png')
os.remove(f'loss_epoch_{epoch}.png')
print("GIF 已生成:training_loss.gif")
print("GIF 已生成:weights_update.gif")
总结
反向传播算法是神经网络训练中的核心技术,它通过计算损失函数相对于每个权重和偏置的梯度,利用梯度下降算法优化网络的参数。理解了反向传播的基本过程,可以进一步扩展到更复杂的网络结构,如卷积神经网络(CNN)和循环神经网络(RNN)。