文章目录
1.图的基本概念
图是由顶点集合及顶点间的关系组成的一种数据结构.
表示为 G = (V, E)。V代表的是顶点集合,E代表边集合
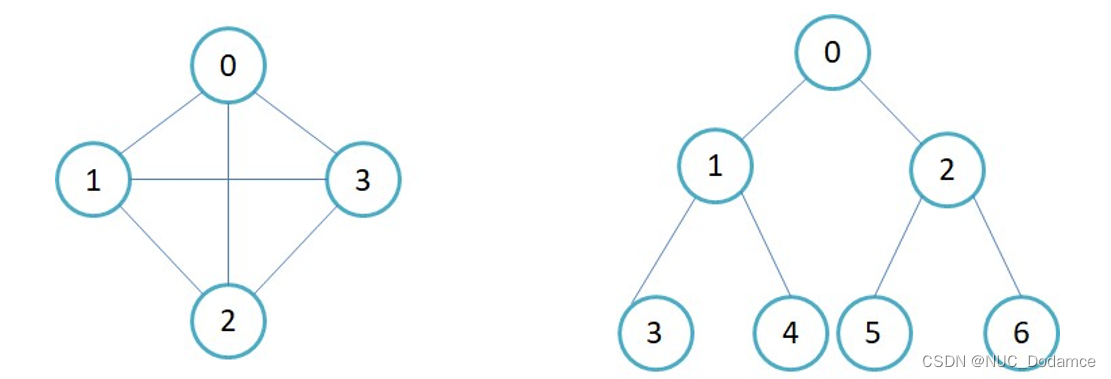
树也是一种特殊的图,这个图无环.
树关注的时节点存的值,图更关注的是顶点及边的权值。
权值:边中的附带的数据信息.
顶点和边:图中结点称为顶点,第i个顶点记作vi。两个顶点vi和vj相关联称作顶点vi和顶点vj之间有一条边,图中的第k条边记作ek,ek = (vi,vj)或<vi,vj>.
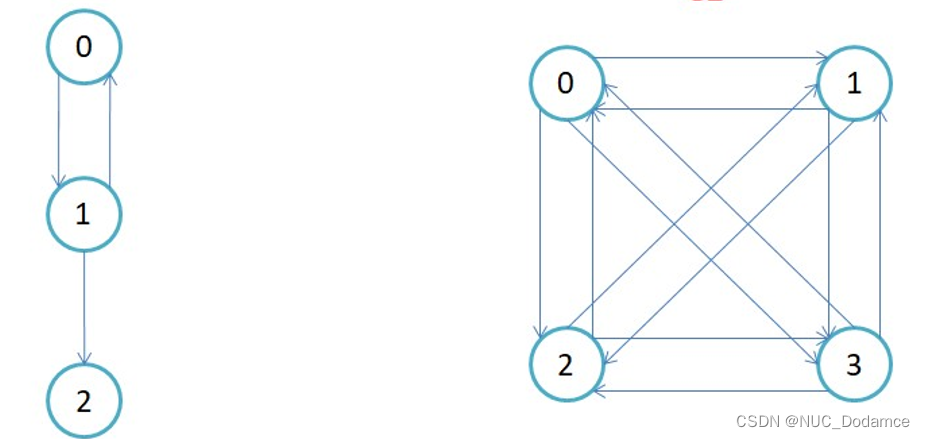
有向图和无向图
有向图:顶点对<x, y>是有序的,顶点对<x,y>称为顶点x到顶点y的一条边(弧),<x, y>和<y, x>是两条不同的边。
eg:
无向图:顶点对(x, y)是无序的,顶点对(x,y)称为顶点x和顶点y相关联的一条边,这条边没有特定方向,(x, y)和(y,x)是同一条边。
完全图
在有n个顶点的无向图中,若有n * (n-1)/2条边,即任意两个顶点之间有且仅有一条边,则称此图为无向完全图;在n个顶点的有向图中,若有n * (n-1)条边,即任意两个顶点之间有两条边,且仅这两条边方向相反,则称此图为有向完全图。
邻接顶点
无向图中:两个顶点U、V有一条边连接。成为U、V互为临界顶点。
有向图中:两个顶点U、V。若是U指向V,则称为U邻接到V,V邻接自顶点U。并称这条边与顶点U、V相关联。
顶点的度
顶点V的度指的是与它相关联的边的条数。
特殊:
- 对于有向图,顶点的度等于该顶点的入度+出度。
出度:从顶点出去的边的条数。
入度:指向这个顶点的边数。 - 对于无向图:入度=出度=顶点的度
路径
从顶点U到顶点V的一组边称为路径。路径不止一条。
路径长度:对于不带权图为路径的边个数。带权图为路径所有边权值的和
最短路径:所有路径,路径长度最小的路径。
简单路径与回路:
- 简单路径:路径上经过顶点不重复。
- 回路:路径上经过的顶点有重复。
子图、连通图、强连通图
两张图A、B,若A的顶点时B的部分顶点,A的边是B的部分边,则称为A是B的子图。
连通图:无向图中,若顶点A、B存在路径,称为A、B连通。若图中的任意两点都是连通的,则称此图为连通图。
强连通图:有向图中,若图中的任意两点都是连通的(A指向B,且B指向A),则称此图为连通图。
生成树
无向图中一个连通图的最小连通子图称为生成树。(用最少的边把所有顶点连接起来)。n个顶点的连通图的生成树有n-1条边。
最小生成树:所有生成树中,路径长度最小的生成树。
2.图的存储结构
因为图中既有节点,又有边(节点与节点之间的关系),因此,在图的存储中,只需要保存:节点和边的关系即可。
节点通过数组保存,边的关系通过下面的方式保存
图的创建
可以通过输入的方式来创建,或者是通过文件的方式来读取。
这里采用手动添加边来创建图,方便测试.
邻接矩阵
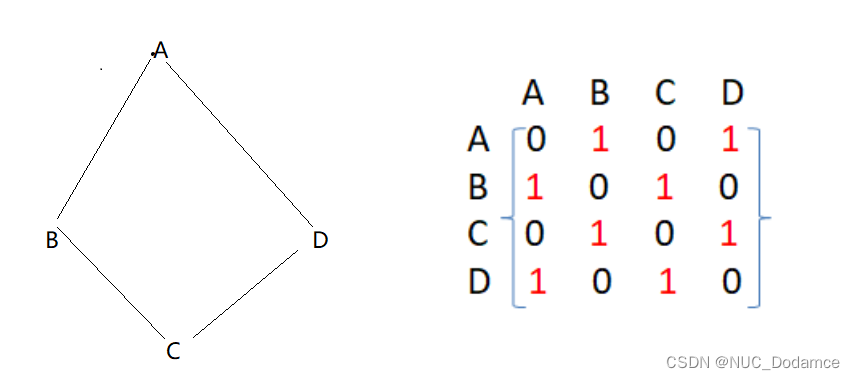
邻接矩阵(二维数组)即是:先用一个数组将定点保存,然后采用矩阵来表示节点与节点之间的关系。
eg:
如果矩阵位置为0代表无关,位置为1代表连接。A对应的下标为0,D对应的下标为3。这里采用map映射的方式来建立顶点与顶点下标的关系.
容易得出:无向图为对称矩阵。
此外:如果这个图是带权图,则矩阵内的数据为所带权值
临界矩阵的存储方式的优点:
- 非常适合边比较多的情况。
- O(1)判断两个节点的连接关系。
不足:
- O(N)查找一个节点连接的所有边。(N为节点个数)。
C++邻接矩阵创建图
#pragma once
#include<vector>
#include<map>
#include<iostream>
//v:顶点 w:权值 max_w:最大权值 Direction:判断图是有向图还是无向图
namespace matrix {
//邻接矩阵保存边关系
template<class v, class w, w max_w = INT_MAX, bool Direction = false>
class Graph {
private:
std::vector<v>_vertexs;//顶点集合
std::map<v, int>_indexMap;//顶点与下标的映射
std::vector<std::vector<w>>_matrix;//邻接矩阵
//获取顶点下标
size_t GetPointIndex(const v& point) {
auto ptr = _indexMap.find(point);
if (ptr != _indexMap.end()) {
return ptr->second;
}
else {
throw std::invalid_argument("顶点不存在");
return -1;
}
}
public:
//图的创建
Graph(std::vector<v>& points) {
_vertexs.resize(points.size());
for (size_t i = 0; i < points.size(); i++) {
_vertexs[i] = points[i];
_indexMap[points[i]] = i;
}
_matrix.resize(points.size());
//邻接矩阵
for (int i = 0; i < _matrix.size(); i++) {
_matrix[i].resize(points.size(), max_w);
}
}
//添加边关系,输入两个点,以及这两个点连线边的权值。
void AddEdge(const v& src, const v& det, const w& weight) {
size_t posSrc = GetPointIndex(src);
size_t posDet = GetPointIndex(det);
//区分有向图与无向图
_matrix[posSrc][posDet] = weight;
if (Direction == false) {
//无向图,添加两条边关系
_matrix[posDet][posSrc] = weight;
}
}
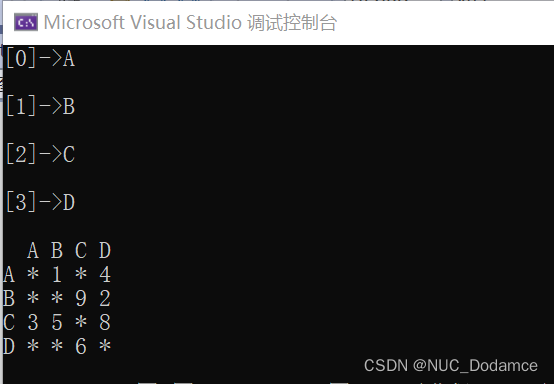
void Print() {
//打印顶点对应坐标
for (size_t i = 0; i < _vertexs.size(); i++) {
std::cout << "[" << i << "]" << "->" << _vertexs[i] << std::endl;
std::cout << std::endl;
}
//打印边
std::cout << " ";
for (int i = 0; i < _vertexs.size(); i++) {
std::cout << _vertexs[i] << " ";
}
std::cout << std::endl;
//打印矩阵
for (size_t i = 0; i < _matrix.size(); i++) {
std::cout << _vertexs[i] << " ";
for (size_t j = 0; j < _matrix[i].size(); j++) {
if (_matrix[i][j] == max_w) {
std::cout << "*" << " ";
}
else {
std::cout << _matrix[i][j] << " ";
}
}
std::cout << std::endl;
}
}
};
}
#include"Graph.h"
using namespace std;
void TestGraph() {
vector<char>points = { 'A','B','C','D' };
matrix::Graph<char, int, INT_MAX, true>graph(points);
graph.AddEdge('A', 'B', 1);
graph.AddEdge('A', 'D', 4);
graph.AddEdge('B', 'D', 2);
graph.AddEdge('B', 'C', 9);
graph.AddEdge('C', 'D', 8);
graph.AddEdge('C', 'B', 5);
graph.AddEdge('C', 'A', 3);
graph.AddEdge('D', 'C', 6);
graph.Print();
}
int main() {
TestGraph();
}
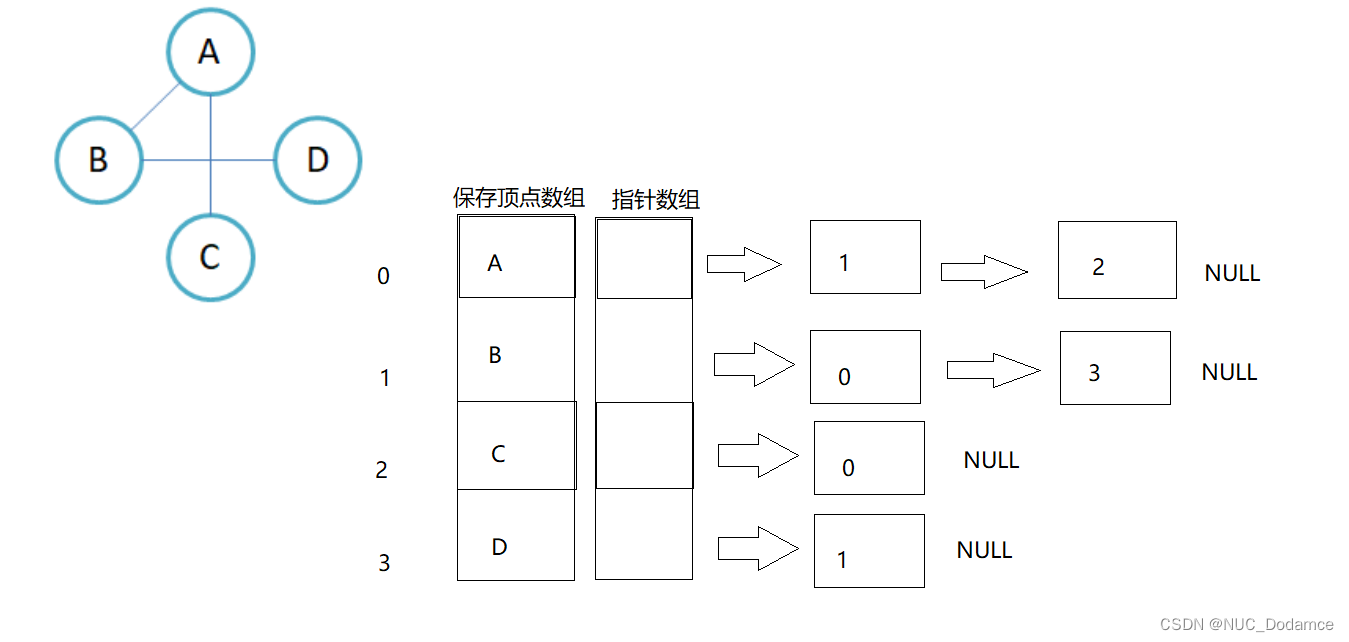
邻接表
使用数组表示顶点的集合,使用链表表示边的关系。
创建指针数组,自己连接的顶点挂在下面。同样的,对节点进行编号
邻接表的优点:
- 适合保存稀疏的边关系。
- 适合查找一个顶点连接出的边
不足:
- 不适合确定两个顶点是否相连,判断权值。
注意:如果图是有向图,则如果使用邻接表存储边的关系,需要保存出边表和入边表。
C++邻接表创建图
#pragma once
#include<vector>
#include<map>
#include<iostream>
//v:顶点 w:权值 max_w:最大权值 Direction:判断图是有向图还是无向图
//邻接表保存边关系
namespace link_table {
template<class w>
struct Edge{
int detPos;
int srcPos;
w weight;
Edge<w>* next;
Edge(int _srcPos, int _detPos, const w& _weight)
:detPos(_detPos), srcPos(_srcPos), weight(_weight),next(nullptr)
{}
};
template<class v, class w, bool Direction = false>
class Graph {
typedef Edge<w> Edge;
private:
std::vector<v>_vertexs;//顶点集合
std::map<v, int>_indexMap;//顶点与下标的映射
std::vector<Edge*>_tables;//邻接表
//获取顶点下标
size_t GetPointIndex(const v& point) {
auto ptr = _indexMap.find(point);
if (ptr != _indexMap.end()) {
return ptr->second;
}
else {
throw std::invalid_argument("顶点不存在");
return -1;
}
}
public:
//图的创建
Graph(std::vector<v>& points) {
_vertexs.resize(points.size());
for (size_t i = 0; i < points.size(); i++) {
_vertexs[i] = points[i];
_indexMap[points[i]] = i;
}
_tables.resize(points.size(), nullptr);
}
//添加边关系,输入两个点,以及这两个点连线边的权值。
void AddEdge(const v& src, const v& det, const w& weight) {
size_t posSrc = GetPointIndex(src);
size_t posDet = GetPointIndex(det);
Edge* edge = new Edge(posSrc, posDet, weight);
//头插
edge->next = _tables[posSrc];
_tables[posSrc] = edge;
if (Direction == false) {
//有向图
Edge* edge = new Edge(posDet, posSrc, weight);
edge->next = _tables[posDet];
_tables[posDet] = edge;
}
}
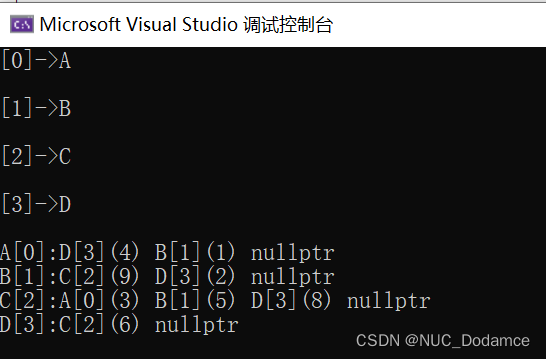
void Print() {
//打印顶点对应坐标
for (size_t i = 0; i < _vertexs.size(); i++) {
std::cout << "[" << i << "]" << "->" << _vertexs[i] << std::endl;
std::cout << std::endl;
}
for (size_t i = 0; i < _tables.size(); i++) {
std::cout << _vertexs[i] << "[" << i << "]:";
Edge* node = _tables[i];
while (node != nullptr) {
std::cout << _vertexs[node->detPos] <<
"[" << node->detPos << "]" << "(" << node->weight << ")" << " ";
node = node->next;
}
std::cout << "nullptr" << std::endl;
}
}
};
}
void TestGraph2() {
vector<char>points = { 'A','B','C','D' };
link_table::Graph<char, int, true>graph(points);
graph.AddEdge('A', 'B', 1);
graph.AddEdge('A', 'D', 4);
graph.AddEdge('B', 'D', 2);
graph.AddEdge('B', 'C', 9);
graph.AddEdge('C', 'D', 8);
graph.AddEdge('C', 'B', 5);
graph.AddEdge('C', 'A', 3);
graph.AddEdge('D', 'C', 6);
graph.Print();
}
int main() {
//TestGraph();
TestGraph2();
}
3.图的遍历
4.最小生成树算法(Kruskal、 Prim算法)
5.最短路径问题(Dijkstra,Bellman-Ford,Floyd-Warshall算法 )
Dijkstra,Bellman-Ford,Floyd-Warshall算法
6.代码位置
图文参考了《算法导论》和《殷人昆 数据结构:用面向对象方法与C++语言描述(第二版)》