论文地址:SDA-FC: Bridging federated clustering and deep generative model - ScienceDirect
代码地址:https://github.com/Jarvisyan/SDA-FC
摘要
联邦聚类(FC)是集中式聚类在联邦环境中的扩展。关键在于如何在不共享私人数据的情况下构建全局相似度度量,因为本地相似度可能不足以正确地对本地数据进行分组,而由于隐私限制,无法直接测量跨客户端的样本相似度。显然,分析联邦聚类最直接的方法是采用从集中式聚类方法扩展而来的方法,如K均值(KM)和模糊C均值(FCM)。然而,这些方法容易受到客户端之间非独立同分布(non-IID)数据的影响。为了解决这个问题,作者提出了一种简单且有效的联邦聚类框架,结合生成对抗网络(GAN),命名为合成数据辅助的联邦聚类(SDA-FC)。该方法在每个客户端本地训练生成对抗网络,并将生成的合成数据上传到服务器,在服务器上对合成数据执行KM或FCM。合成数据可以使模型免受非IID问题的影响,并帮助更有效地捕捉全局相似性特征,而无需共享私人数据。综合实验结果揭示了SDA-FC的优势,包括在解决非IID问题和设备故障方面的优越表现。
引言
在隐私问题日益受到关注的时代,联邦学习(FL)[29] 引起了广泛的关注,并在多个领域得到了应用,包括自动驾驶、智能医疗、智能城市和物联网数据等。其目标是在不共享私人数据的情况下,通过融合多个在客户端设备上训练的本地模型来训练全局模型。虽然FL在独立同分布(IID)场景中表现出色,但客户端设备之间的本地数据分布通常偏离IID场景。这种现象被称为非独立同分布问题(non-IID问题)或数据异质性,它可能会妨碍收敛并对模型性能产生不利影响[25]。在非IID场景下,一种自然的解决方法是放弃传统的单中心方法,即专注于训练单一的全局模型,而是构建一个多中心框架,利用客户端聚类[13]或数据聚类来增强协作[8,36,5]。对于客户端聚类,其基本思想是每个客户端可能来自一个特定的分布。因此,应该使用同一聚类中的客户端共同训练一个特定的全局模型。然而,每个客户端中的每个样本也可能来自特定的分布。因此,数据聚类,也称为联邦聚类(FC),可以更有利于客户端之间的协作[36]。其目标是基于全局相似度度量对数据进行聚类,同时保持数据的本地性[36]。
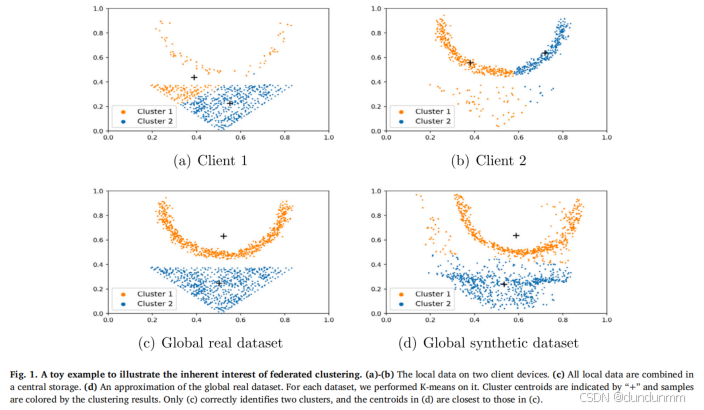
除了在缓解非IID问题中的作用外,联邦聚类本身也是一个引人注目的研究领域。如图1所示,单纯依靠本地相似度无法准确地恢复本地数据分组,而全局视角在这方面表现更为出色。然而,由于本地客户端数据的保密性,获取全球真实数据是不可行的。
因此,关键在于如何在不共享私人数据的情况下衡量全局相似度。为了解决这个问题,之前的工作已将经典的集中式聚类算法(如K均值(KM)[28]和模糊C均值(FCM)[3])进行适配,以应用于联邦设置,从而得到了k-FED [8]和联邦模糊C均值(FFCM)[36]。它们的基本思路是类似的:交替估计本地聚类中心和全局聚类中心,换句话说,通过本地私人数据挖掘本地聚类中心并将其上传到服务器,在服务器上运行KM以构建k个全局聚类中心来容纳全局相似度信息,然后将这些信息传递给客户端。最后,每个客户端可以从服务器下载全局聚类中心,并根据与这些聚类中心的接近度对本地数据进行标注,遵循最近邻规则。然而,得到的全局聚类中心可能会非常敏感,并容易受到不同非IID级别的影响,从而损害模型的鲁棒性和性能。给定一个联邦数据集,非IID级别仅取决于本地数据分布,而非全局数据分布。因此,如果能够构建出全球数据的良好近似,模型的性能可能对不同的非IID级别不敏感。此外,这种近似能够在不共享私人数据的情况下增强捕捉全局相似性特征的能力。基于这一思路,作者提出了一种简单有效的联邦聚类框架,结合生成对抗网络(GAN)[14],命名为合成数据辅助的联邦聚类(SDA-FC)。它包括两个主要步骤:全局合成数据构建和聚类分配。在第一步中,中央服务器利用多个从本地数据训练的本地GAN构建全局合成数据集。在第二步中,中央服务器首先对全局合成数据集执行KM或FCM,得到k个全局聚类中心,然后将其分发给客户端。随后,基于最近邻规则进行聚类分配。如图1所示,本地聚类中心(图1(a)和图1(b))与全局聚类中心(图1(c))有显著差异,后者无法通过简单地对前者执行KM来准确近似。值得注意的是,全局合成数据(图1(d))很好地近似了全球真实数据,其中由合成数据集得到的聚类中心与从真实全局数据中得到的聚类中心非常接近。为了进一步探索联邦聚类与集中式聚类之间的差距,在联邦设置下对k-FED和FFCM进行了实验,并在集中设置下执行了KM和FCM。如表1所示,二者之间存在差距,但通过该方法该差距被缩小了。
模型
SDA-FC框架
SDA-FC由两个主要步骤组成:全局合成数据构建和聚类分配。在第一步中,每个客户端本地训练深度生成模型(例如生成对抗网络(GAN)[14]),然后将生成的合成数据上传到服务器进行聚合。在第二步中,对聚合后的合成数据执行K-means(KM)[28]或模糊C均值(FCM)[3]聚类,构建出k个全局聚类质心。最后,每个客户端可以从服务器下载全局聚类质心,并根据最近邻规则对其本地数据进行标签分配。
全局合成数据构建
给定一个现实世界的数据集 𝑋 ∼ ℙ,其中数据集分布在𝑚个客户端之间,即 并且 𝑋(𝑖) ∼ ℙ(𝑖)。首先,每个客户端𝑖(𝑖 = 1, 2, ⋯, 𝑚)从中央服务器下载初始的深度生成模型,并用本地数据 𝑋(𝑖) 训练该模型。然后,每个客户端使用训练好的模型 𝐺(𝑖) 生成一个与 𝑋(𝑖) 大小相同的合成数据集
,并将该合成数据集上传到中央服务器。最后,通过聚合所有上传的数据集,可以获得全局合成数据集 𝑋,即
。
3.1.2 聚类分配
作为一个通用的联邦聚类框架,可以简单地将SDA-FC与一些集中式聚类方法结合,如KM和FCM,从而得到两个具体方法,分别是SDA-FC-KM和SDA-FC-FCM。具体来说,中央服务器首先在全局合成数据集上执行KM或FCM,得到k个全局质心。然后,每个客户端下载这些质心,并通过最近邻规则对本地数据进行标签分配,从而得到最终的聚类结果。
3.2 基于GAN的SDA-FC实例化
近年来,深度生成模型因其在各种数据模态生成方面的卓越能力而受到广泛关注[18,43]。FID——Frechet Inception Distance通过利用真实数据的统计信息来评估合成数据的质量,FID值越低表示生成样本的质量和多样性越高。如广泛认可的[18,43],GAN和扩散模型在FID分数上表现最为突出。尽管扩散模型在生成能力上优越,但其复杂的数学细节[43]会极大地增加我们框架的复杂性,而其时间消耗较长的生成过程[40]会增加客户端设备的计算负担。因此,本工作选择使用GAN来构建合成数据并实例化SDA-FC。
标准的GAN架构[14]包含两个网络:生成器和判别器。这两个网络通过博弈的方式不断相互改进。生成器的目标是生成与真实数据相似的合成样本,从而欺骗判别器,而判别器的目标是区分真实样本和生成样本。博弈的结束条件是判别器无法再区分真实样本和生成样本,表示生成器已经学习到了真实数据分布并达到了理论上的全局最优。
正式地,标准GAN的目标函数定义为:
其中,𝐺是生成器,它输入噪声 𝑧 并输出生成的样本,𝒩是高斯分布,𝐷是判别器,它输入一个样本并输出一个标量,表示区分生成样本与真实样本,𝑝𝑟 是真实数据的分布。虽然GAN在各种应用中表现出色,但对抗训练以其不稳定性和容易发生模式崩溃(mode collapse)而闻名[30],这导致生成样本质量高但多样性差。模式崩溃意味着模型只能捕捉到真实数据特征的一部分。为了解决这个问题,Mukherjee等[31]向生成器的输入中引入了一个额外的类别变量,从而促进潜在空间中更加清晰的聚类结构,并增强样本多样性。
为了减轻SDA-FC实例中的模式崩溃,作者也使用了离散和连续变量的混合作为生成器的输入,遵循[31]的方法。新的目标函数定义为:
其中,𝒰 是一个均匀随机分布,其最低值为 1,最高值为 𝑘,𝑒𝑢 是一个one-hot向量,其中第𝑢个元素为1。
3.3 理论分析
在SDA-FC中,一个关键的见解是,尽管由于隐私约束无法获得全球真实数据,但可以通过共享本地合成数据来近似全局真实数据。因此,关于本地合成数据是否能代表全球真实数据的稳健理论分析,对于保证模型的可靠性至关重要。
在概率机器学习中,分布通常可以通过多个分布的线性组合来表示[24]。在这里,假设全球真实数据分布可以表示为本地数据分布的混合,即 ℙ = ∑𝑚 𝑖=1 𝑤(𝑖) ℙ(𝑖),其中 𝑤(𝑖) ≥ 0,且 ∑𝑚 𝑖=1 𝑤(𝑖) = 1,则全球真实数据分布也可以表示为本地合成数据分布的混合,当 ℙ̂ (𝑖) 和 ℙ(𝑖) 相等时,如定理1所述。
引理1 [14]:GAN的对抗训练能够实现全局最优,当且仅当合成数据分布与真实数据分布相等。
定理1:如果本地合成数据分布与真实数据分布相同,即 ℙ̂ (𝑖) = ℙ(𝑖),𝑖 = 1, 2, ⋯, 𝑚,则全球真实数据分布 ℙ 可以表示为本地合成数据分布的混合。
证明:在SDA-FC中,每个GAN都是使用本地数据独立训练的,这意味着GAN的理论性质(引理1)仍然成立,即 ℙ̂ (𝑖) = ℙ(𝑖),𝑖 = 1, 2, ⋯, 𝑚。因此,ℙ = ∑𝑚 𝑖=1 𝑤(𝑖) ℙ(𝑖) = ∑𝑚 𝑖=1 𝑤(𝑖) ℙ̂ (𝑖)。此证明完毕。
实验
聚类性能
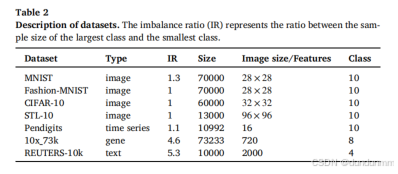
联邦聚类作为一个新兴领域,目前尚缺乏标准化的评估框架。例如,在研究 [8,36,38] 中,使用的基准数据集并不一致,这使得直接比较变得困难。因此,基准方法的代码可用性和实现的简便性成为了主要考虑因素,这也促使选择了 k-FED [8]、联邦模糊 c-均值(FFCM)[36] 和 FedMAvg [38] 作为基准方法。此外,为了将联邦聚类的性能与集中式聚类进行对比,作者还报告了 K-均值(KM)、模糊 c-均值(FCM)和正交非负矩阵分解(ONMF)[39] 在集中式场景下的数值结果,分别表示为 KM_central、FCM_central 和 ONMF_central。在所有实验中,基于 FCM 的方法的默认模糊度设置为 1.1。
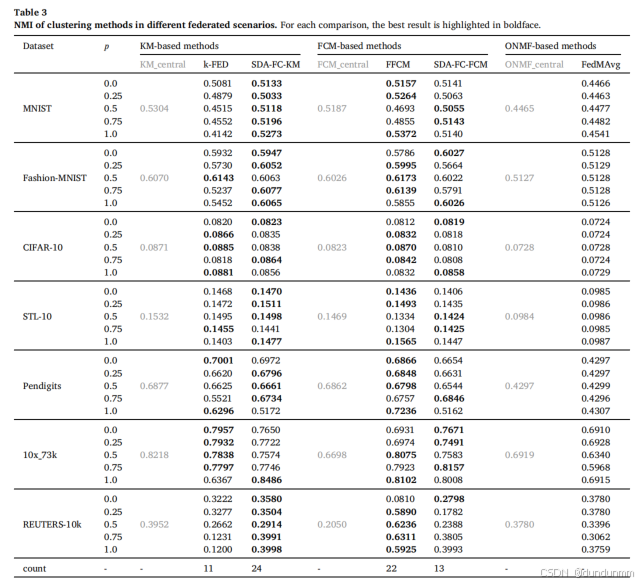
基于 NMI [37] 和 Kappa [23] 的聚类性能见表 3 和表 4。从中可以观察到:
- 对于基于 KM 的方法,两项指标一致表明提出的方法在有效性和鲁棒性上均优于 k-FED。对于基于 FCM 的方法,两项指标给出了不同的排名。虽然 NMI 是最常用的指标,但近年来的研究强调了它的局限性,因此 Kappa 被认为是一个更可靠的替代方案 [23,42]。在此,作者还展示了新的案例,表明 NMI 无法准确反映聚类结果的性能。如图 2 所示,SDA-FC 提供了与真实标签更为一致的聚类结果,但 NMI 排名较低(FFCM 为 0.6806,SDA-FC 为 0.6654),这一结果是意外的。相比之下,Kappa 给出了更合理的排名(FFCM 为 0.6523,SDA-FC 为 0.6611)。此外,在 CIFAR-10 数据集上,作者在集中式场景下建立了一个基准,与真实标签计算出的真实聚类中心对比,基于从本地数据到聚类中心的余弦距离来分配聚类。直观上,基于 KM 或 FCM 的方法无法超越该基准。然而,NMI 给出的排名正好相反(基准为 0.1009,FFCM 在模糊度为 2 且 p = 0.75 时为 0.1051,FFCM 在模糊度为 2 且 p = 1 时为 0.1059),而 Kappa 给出了更合理的值(基准为 0.1992,FFCM 在模糊度为 2 且 p = 0.75 时为 0.1634,FFCM 在模糊度为 2 且 p = 1 时为 0.1854)。因此,对于基于 FCM 的方法,作者提出的方法在有效性和鲁棒性方面表现优秀。
- 存在 KM 基于(FCM 基于)联邦聚类和 KM 基于(FCM 基于)集中式聚类之间可识别的差距,但 SDA-FC 缓解了这个差距。
- 有趣的是,FFCM 在 REUTERS-10k 数据集上,在 IID 场景(𝑝 = 0)下的表现明显不如其集中式对应方法,而在非 IID 场景(𝑝 > 0)下,情况显著反转。这表明集中式训练并不总是最优选择,在某些情况下,战略性的分布式训练可能会带来更好的聚类性能。
- 尽管 FedMAvg 在多种非 IID 水平下表现出更大的鲁棒性,但与 SDA-FC 相比,它的表现较差,并且在通信上存在低效(稍后将详细说明)。
之前没有看过这个领域的聚类,刚好看GAN发现了这一篇,学习一下。。