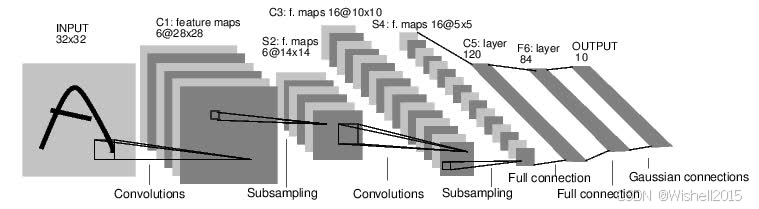
CNN张量输入形状和特征图
这个是比较容易理解的张量的解释,比较直观
卷积神经网络
在这个神经网络编程系列中,我们正在逐步构建一个卷积神经网络(CNN),所以让我们看看CNN的张量输入。
在最后两篇文章中,我们介绍了张量和基本的张量属性秩、轴和形状。如果你还没有看过那些文章,我强烈建议你去查看。
我现在想做的是,用一个实际的例子来应用秩、轴和形状的概念。为此,我们将考虑将图像输入作为CNN的张量。
卷积神经网络是图像识别任务的首选网络,因为它们非常适合检测空间模式。
记住,张量的形状编码了关于张量轴、秩和索引的所有相关信息,所以我们将在示例中考虑形状,这将使我们能够计算出其他值。让我们开始。
CNN输入的形状
CNN输入的形状通常有四个长度。这意味着我们有一个秩为4的张量,有四个轴。张量形状中的每个索引代表一个特定的轴,每个索引处的值给出了相应轴的长度。
张量的每个轴通常代表输入数据的某种现实世界或逻辑特征。如果我们理解这些特征及其在张量中的轴位置,那么我们就可以很好地理解张量数据结构的整体。
为了分解这一点,我们将从右到左反向工作,考虑轴。记住,我们从最后一个轴开始,这是我们将要开始的地方,是实际数字或数据值所在的位置。
如果我们沿着最后一个轴运行并在那里检查一个元素,我们将看到一个数字。如果我们沿着任何其他轴运行,元素是多维数组。
对于图像,原始数据以像素的形式出现,由数字表示,并使用两个维度(高度和宽度)布局。
图像高度和宽度
为了表示两个维度,我们需要两个轴。
图像的高度和宽度在最后两个轴上表示。这里可能的值是28 x 28,就像我们将在CNN项目中使用的fashion-MNIST数据集中的图像数据一样,或者是VGG16神经网络使用的224 x 224图像大小,或者我们可以想象的任何其他图像尺寸。
图像颜色通道
下一个轴代表颜色通道。这里典型的值是3,对于RGB图像,或者是1,如果我们处理的是灰度图像。这种颜色通道的解释只适用于输入张量。
我们将在片刻后揭示,这个轴的解释在张量通过卷积层后会发生变化。
到目前为止,使用最后三个轴,我们已经将一个完整的图像表示为一个张量。我们有了颜色通道和高度和宽度,都以张量形式布局,使用了三个轴。
在这一点上,为了访问数据,我们需要三个索引。我们选择一个颜色通道,一个高度和一个宽度,以到达一个特定的像素值。
图像批次
这使我们来到了四个轴中的第一个,它代表批量大小。在神经网络中,我们通常使用样本的批次而不是单个样本,所以这个轴的长度告诉我们批次中有多少个样本。
这使我们能够看到,整个图像批次使用一个秩为4的张量表示。
假设我们有一个给定张量的形状[3, 1, 28, 28]。使用形状,我们可以确定我们有三个图像的批次。
[批次大小,颜色通道,高度,宽度]
每张图像有一个单一的颜色通道,图像的高度和宽度分别是28 x 28。
- 批次大小
- 颜色通道
- 高度
- 宽度
这给我们一个单一的秩为4的张量,最终将流经我们的卷积神经网络。
给定这样的图像张量,我们可以使用四个索引导航到批次中特定图像的特定颜色通道的特定像素。
NCHW vs NHWC vs CHWN
在阅读API文档和学术论文时,通常可以看到B被N替换。N代表批次中的_样本数量_。
此外,我们在实际中经常遇到的另一个区别是维度的_重新排序_。常见的排序如下:
-
NCHW -
NHWC -
CHWN
正如我们所看到的,PyTorch使用NCHW,而TensorFlow和Keras默认使用NHWC(可以配置)。最终,选择使用哪一个主要取决于性能。一些库和算法更适合这些排序中的一种或另一种。
输出通道和特征图
让我们看看张量通过卷积层转换后,颜色通道轴的解释如何变化。
假设我们有一个张量,包含来自单个28 x 28灰度图像的数据。这给我们提供了以下张量形状:[1, 1, 28, 28]。
现在假设这个图像被传递到我们的CNN,并通过第一个卷积层。当这种情况发生时,我们的张量形状和底层数据将被卷积操作改变。
卷积改变了高度和宽度维度以及通道数量。输出通道的数量根据卷积层中使用的过滤器数量而变化。
假设我们有三个卷积过滤器,让我们看看通道轴会发生什么变化。
由于我们有三个卷积过滤器,我们将有三个来自卷积层的通道输出。这些通道是卷积层的输出,因此被称为输出_通道,而不是_颜色通道_。
三个过滤器中的每一个都对原始的单一输入通道进行卷积,产生三个输出通道。输出通道仍然由像素组成,但像素已经被卷积操作修改。根据过滤器的大小,输出的高度和宽度维度也会改变,但我们将在未来的文章中讨论这些细节。
特征图
有了输出通道,我们不再有颜色通道,而是有我们称之为_特征图_的修改后的通道。这些所谓的特征图是使用输入颜色通道和卷积过滤器进行卷积的结果。
特征图是由卷积产生的输出通道。
“特征”这个词被使用是因为输出代表了图像中的特定特征,例如边缘,并且这些映射在训练过程中网络学习时出现,并随着我们在网络中深入而变得更加复杂。
总结
我们现在应该对CNN输入张量的总体形状,以及秩、轴和形状的概念如何适用于这种理解有了很好的理解。
当我们开始构建CNN时,我们将在未来的文章中加深对这些概念的理解。在此之前,我们将在下一篇文章中见到你!